Matemáticas de Leonardo

Leonardo da Vinci (1452-1519) es el ejemplo de los científicos del Renacimiento. Este científico, como es conocido, se dedicó a muchos campos de la ciencia: Anatomía, Óptica, Botánica, Biología, Geografía, Geología, Mecánica, Geometría, Pintura, Escultura, Urbanismo, Arquitectura, Astronomía, Náutica, Física, etc. No había quien no animara a investigar sus curiosidades. Tenía que explorar todo.
Aunque es más conocido en las artes, no podemos descartar aportaciones en otros ámbitos. Leonardo fue autodidacta y, a diferencia de otros científicos de entonces, no sabía ni latín ni griego. Sin embargo, esto no significa que sus obras carezcan de una base sólida. Por el contrario, cuando se sumergía en una obra (ciencia) estudiaba en profundidad todas las formas. Su curiosidad era tan grande que dejaba a menudo el trabajo que estaba realizando.
Sabemos que cuando regresó a Florencia en 1501, tras estar con Luca Pacioli, se sumergió en la Geometría. Mientras tanto, el tímpano del cuadro de Santa Ana no paró de hacer. Desde 1501 se dedicó a la Geometría; entre 1504 y 1506 a la Hidráulica; en 1505 estudió la geometría de los sólidos en un escribo; en 1510 fue atraído por la Anatomía; etc.
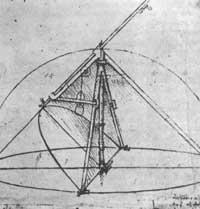
Pero en este artículo queremos mencionar las matemáticas de Leonardo, menos conocida.
El joven Leonardo aprendió mucho en la escuela de Andrea Verrocchio. En el taller de Verrocchio se estudiaba no sólo la pintura, sino también el bronce fundido, la piedra, los planos, la apertura de canales, la construcción de casas, etc. En todas estas “artes”, el conocimiento de la perspectiva también en la pintura tenía gran importancia, se pedía una base científica (sobre todo matemática) enorme. La formación de Leonardo era práctica, fundamentalmente Ingeniero Leonardo, maquinista, no teórica. Por ello, es de su geometría mecánica. Las soluciones que busca son prácticas (que se pueden hacer con herramientas reales) y no teóricas.
Ejemplos de esta tendencia práctica son los estudios sobre la construcción de polígonos regulares inscritos en círculo. En sus escritos aparecen estas imágenes y muchas propiedades. Entre otras cosas, las relativas al cuadro del círculo; la inscripción de los polígonos de 3, 6, 8, 24 (es fácil y Leonardo lo hace con la apertura constante del compás), una aproximación a la construcción de los polígonos regulares (como el pentágono y el haptágono que no se pueden construir directamente mediante reglas y compases, es más difícil de realizar, pero Leonardo tiene suficiente solución cercana).
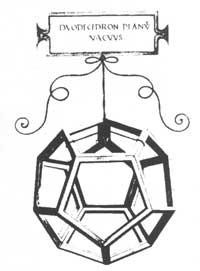
Probablemente serán suyos los llenos y vacíos de poliedros regulares y semi-regulares que ilustran el código “Divina Proportione” que Luca Pacioli ofreció a Ludovico Mairua en 1498. Realiza la dirección del círculo y arroja un cuadratura, círculo o rodillo sobre una recta o un plano. Esta solución supone un desconocimiento del problema teórico. Sin embargo, se entiende desde el punto de vista del ingeniero.
Sin duda, Leonardo debía su sabiduría matemática a Luca Pacioli. Y es que lo consiguió tan pronto como publicaba Summa y luego se reconcilió con su autor. También conoció a Alberto de Sajonia, Jordanus Nemorarius (a quien muchas veces se refería) y Nicolás de Cusa (que sin duda influyó en él). Seguramente no estudió directamente a Arquímedes, pero está claro que lo conoció indirectamente a través de Eutocio y Giorgio Valle.
Es raro que no haya cenado de Leonardo Algebra. ¿Era difícil o demasiado abstracto?. Era, sin embargo, una geometría pura que sustituía el desconocimiento teórico del espacio por su poder visual. Las reflexiones sobre los conceptos básicos de la geometría son muy interesantes, aunque la influencia de Aristóteles y Nicolás de Cusa es evidente.
Leonardo no retrocede ante el uso de conceptos infinitesimales (es el paso al límite). Por ejemplo, propone dividir el centro de gravedad del semicírculo en pirámides (triángulos) de determinación, tantas pirámides como sean necesarias para que la fragilidad de sus bases sea inapreciable y casi directa. Sin embargo, este es un caso excepcional y, en general, los métodos de Leonardo son más simples, correctos y elementales.

Las ideas intuitivas, probablemente, le llevaron a su mayor descubrimiento, a calcular el centro de gravedad de la pirámide. Parece que trasladando al espacio el mismo razonamiento que hizo sobre el centro de gravedad del triángulo del plano, pasando por el tetraedro regular, pudo ubicar su centro de gravedad en el punto de corte de sus ejes (es decir, las rectas que unen un vértice con el centro de gravedad del lado opuesto) y al cuarto de la distancia de la base.


Más tarde descubrió que las rectas que unen los puntos centrales de las esquinas contra un tetraedro se cortan en el centro de gravedad. Finalmente, generalizó el descubrimiento, indicando que el centro de gravedad de cualquier pirámide se encuentra en su eje (de la base a la cuarta parte).
Las investigaciones sobre la transformación recíproca de sólidos se basan en “De transmutationibus geometricis” de Nicolás Cusa, quien aplica los métodos de Valle para resolver problemas enunciados por el cusés (formando la confluencia de varios cubos, convirtiendo un cubo en un prisma y viceversa). Sin embargo, Leonardo también considera transformaciones especiales. Por ejemplo, entre el cubo y la pirámide.
Leonardo también se ocupó de las lumulas de Hipócrates. Además de las numerosas menciones de su Cuadernos, en 1514 intentó escribir un tratado: De ludo geométrico, que quedó incompleto como toda su obra. Se entiende que exista una cierta pasión por el valor estético de las lumulas. De paso, en Occidente descubrió unas proposiciones geométricas que aún no se conocían. Por ejemplo, estableció que la suma de las superficies de las lumulas construidas sobre los lados de los triángulos equiláteros era igual a la del triángulo.
Cabe mencionar la ingeniosa solución mecánica que Leonardo encontró para el problema de Óptica de Al-Hazi con un compás especial. Esta solución de Leonardo indica profundos conocimientos sobre las propiedades de los cortes cónicos. Geométricamente 150 años después fue resuelto por Huygens.
Las investigaciones sobre perspectiva realizadas por Leonardo se publicaron en el “Tratado de la pintura” en 1651.
Hay que decir que a Leonardo se le deben imágenes y proyectos de herramientas matemáticas, compases de proporción y un parabológrafo que utilizó para construir espejos parabólicos.
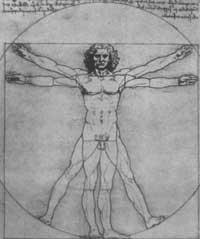
La influencia de las matemáticas también se puede apreciar en sus pinturas. Leonardo codificó las proporciones del cuerpo haciendo la geometría infraestructura de sus pinturas. Su composición responde a un esquema armónico fácilmente localizable, con estructuras radiales, troncos de cono, triángulos, arcos, espirales, trapecios, pentágonos, etc.









