La beauté du chaos
On dit que la science classique se termine quand le chaos est créé. Tandis que les scientifiques essayaient de voir un ordre (une règle représentée par des équations mathématiques de valeur universelle) tout en étudiant les lois de la nature, le monde vivait de dos à l'apparence désordonnée de la réalité.

Les volutes d'une onde, les hauts et les bas de la population, les désordres atmosphériques (aussi bien des falaises côtières que des différentes formes apparaissant dans le réfrigérateur), l'accumulation d'étoiles dans une galaxie et le treillis des vaisseaux sanguins sont des exemples de cette partie irrégulière de la nature. Cette partie discontinue apparaît comme une controverse devant les humains.
Systèmes dynamiques
Pendant des siècles, les phénomènes de la nature ont été analysés dans une perspective analytique. Le système analytique considère en détail chaque partie d'un phénomène. Cependant, cette perspective a des erreurs pour apprendre des phénomènes très difficiles. Une autre solution est l'approche systématique. Selon cela, il est préférable d'avoir un aperçu des phénomènes, même si les détails sont perdus.

L'approche systématique est basée sur la notion de système dynamique. Le système dynamique est une collection d'objets qui sont interconnectés et évoluent au fil du temps selon un ensemble de règles.
Les systèmes dynamiques sont abondants dans la nature. Système écologique (où proies et prédateurs, faim, fléaux, sécheresses, attaques humaines, etc.). existent), est un exemple de systèmes dynamiques. Les relations entre les voisins déterminent si chaque espèce survit ou se perd.
Les scientifiques qui essaient d'apprendre des systèmes dynamiques élaborent des copies simplifiées ou des modèles (corrigées par des équations mathématiques) et essaient de faire fonctionner approximativement comme un système réel. Ils introduisent le modèle sur l'ordinateur et voient comment il évolue au fil du temps et dans quelle mesure il change en changeant les paramètres.
Par exemple, le système écologique peut inclure différents climats, nombre d'habitants, taux de natalité, aliments quotidiens nécessaires, comportement animal, etc. Le modèle peut mettre fin à la perte d'une espèce, quand il y a trop de nourriture pauvre ou de proie, ou quand il y a équilibre entre les espèces. Tout dépend de l'introduction des paramètres.
Parfois, les analystes du système analysent l'état final d'un système et tentent de le reconstruire pour enquêter sur les causes qui ont conduit le système à cette situation. Un exemple célèbre a été le suivant : dans la civilisation maya VIII. Un modèle pour expliquer l'effondrement du XXe siècle.

L'étude moderne du chaos a commencé dans les années 60 avec une découverte désavantageuse: un ensemble d'équations mathématiques d'apparence simple, capable de décrire des systèmes dynamiques créés par des conditions de comportement rigide et initiales. Les petites différences dans la situation initiale engendrent de grandes différences dans l'évolution du système. On l'a appelé effet papillon. Ce mot (au milieu d'une plaisanterie) indique que le mouvement des ailes d'un papillon, réalisé ici et maintenant, influence la climatologie de Pékin du mois suivant.
Dans les années 1970, un groupe de scientifiques a travaillé pour ouvrir la voie au royaume du désordre. Ils étaient mathématiciens, physiciens, biologistes, sociologues, économistes et physiologues. Ils cherchaient des explications sur l'irrégularité qu'ils voyaient dans leurs travaux, en utilisant un nouveau système d'analyse.

Vingt ans plus tard, le terme chaos est devenu une description détaillée d'une tendance (mouvement scientifique). Augmentation des conférences, des programmes de recherche et des publications. Des articles sur l'étrange dynamique d'une balle, ainsi que d'autres sur la mécanique quantique, sont sortis sur une table.
La science du désordre a créé des techniques basées sur l'utilisation des ordinateurs. Ces techniques offrent des images du chaos, des structures fascinantes, hypnotiques, délicates et de difficulté infinie.
En réalité, les modèles mathématiques qui tentent de montrer un système écologique, climatique, économique ou d'autres systèmes de grande difficulté, sont formés par des milliers d'équations et nécessitent beaucoup de temps de traitement par ordinateur.

Cependant, il existe certains modèles qui sont formulés avec peu de relations et qui ont une grande difficulté.
Un modèle mathématique simple peut être divisé d'une valeur initiale que nous appellerons de début et, après quelques calculs, créer une valeur finale: Finition. Cette dernière valeur est introduite dans le modèle comme valeur initiale et ainsi de suite. La réintroduction de la sortie comme entrée est appelée réalimentation. Il y a une réalimentation, par exemple, quand un microphone prend la sortie de l'amplificateur. En fin de compte, l'effet
est insoutenable.
Initiale = 1,1
et calculons votre carré. On calcule à nouveau le carré de la valeur du Xbucal obtenu, etc. La séquence des nombres obtenus sera la suivante: 1,21; 1,4641; 2,14358881;...
Continuez à retirer vos comptes. Mais lentement les nombres sont de plus en plus
grands, sans limites.
Initial = 0,99
avec la séquence suivante: 0,9801; 0,96059601; 0,922744694; ... lentement, mais cette succession s'approche de zéro. Il est surprenant que les nombres si proches les uns des autres (1,1 et 0,99) aient un comportement si
différent.
Finition = (de départ)2
La norme a été utilisée. Nous pouvons également utiliser d'autres formules qui nous arrivent et voir le comportement. Par exemple :
Finition = R.Xdébut (1 - De début)

relation, où R est un nombre qui est choisi au début. Cette formule est appelée équation logistique et était l'une des premières à être étudiée.
Au lieu d'essayer d'interpréter la succession de nombres que vous obtenez, vous pouvez jouer graphiquement. Sur l'axe horizontal nous placerons les valeurs de R, par exemple entre 2 et 5. Sur l'axe vertical pour le point de départ
(Initial = 0,6, p. ex.)
Nous situerons la succession des valeurs obtenues. La figure 1 montre la représentation graphique du résultat. Des branches se séparent à l'infini.
Attracteur de Lorenz

En 1963, Edwarz Lorenz analysait les tourbillons qui se produisent par chauffage et refroidissement des couches atmosphériques. Le phénomène modélisé par un système d'équations, qui semblait simple, représentait graphiquement le parcours de la particule laissée dans un tourbillon.
L'image obtenue, aujourd'hui classique, a dévoilé la structure difficile cachée dans les équations et est devenu le drapeau des premiers examinateurs du chaos. La figure 2 montre l'attraction de Lorentz.
En tant que météorologue, Lorenz a publié sa découverte dans le Journal of the Atmospheric Sciences, loin des mains des physiciens, des biologistes et des ingénieurs.
Fractales

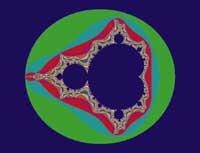
Benoit Mandelbrot, mathématicien chercheur qui a travaillé dans l'entreprise IBM, a inventé un nouvel élément qui plus tard appelé fractale.
Mandelbrot a vu une image connue à différents endroits: à la hauteur des prix des marchandises, il a surpris les ingénieurs en problèmes de bruits sur les lignes téléphoniques, etc. Dans tous, on voyait la même caractéristique, une signature qui dénonçait le chaos. Quand on analysait plus en détail, les règles de l'évolution étaient de plus en plus difficiles.
Les artistes trouvent la beauté idéale en images classiques comme les lignes, les plans et les sphères, une structure harmonieuse. Cependant, la réalité montre une géométrie complexe, cassée et mélangée. Discontinuités, bruits soudains et comportements étranges ont été décrits par Mandelbrot par des concepts mathématiques abstraits. Le fractale nous donne une voie pour modeler cette réalité complexe.

Les courbes fractales peuvent être générées par un ordinateur et ont des formes fascinantes, comme le montre les figures 3-10. Coraux, galaxies et dragons fractales représentent des créatures aussi complexes que celles qui nous entourent.
La figure 11 montre une image de la planète Aqua-Tor. C'est une planète en forme de toroïdes dont la surface marine est couverte par un plasma fractale. Si le lecteur se fixe sur elle, vous verrez bientôt quelques espèces qui luttent pour survivre à Acua-Torre.





