La bellesa del caos
Es diu que la ciència clàssica acaba quan es crea el caos. Mentre els científics tractaven de veure un ordre (una regla representada per equacions matemàtiques de valor universal) mentre estudiaven les lleis de la Naturalesa, el món vivia d'esquena a l'aparença desordenada de la realitat.

Les volutes d'una ona, els alts i baixos de la població, els desordres atmosfèrics (tant dels penya-segats costaners com de les diferents formes que apareixen en la nevera), l'acumulació d'estrelles en una galàxia i l'entramat de vasos sanguinis són exemples d'aquesta part irregular de la Naturalesa. Aquesta part discontínua apareix com una controvertida davant els éssers humans.
Sistemes dinàmics
Durant segles s'han analitzat els fenòmens de la Naturalesa des d'una perspectiva analítica. El sistema analític considera detalladament cada part d'un fenomen. No obstant això, aquesta perspectiva té errors per a aprendre fenòmens molt difícils. Una altra solució és l'enfocament sistemàtic. Segons això, el millor és tenir una visió general dels fenòmens, encara que es perdin detalls.

L'enfocament sistemàtic es basa en la noció de sistema dinàmic. El sistema dinàmic és una col·lecció d'objectes que estan interrelacionats i evolucionen al llarg del temps segons un conjunt de normes.
Els sistemes dinàmics són abundants en la Naturalesa. Sistema ecològic (on preses i predadors, fam, plagues, sequeres, atacs humans, etc.). existeixen), és un exemple de sistemes dinàmics. Les relacions entre els veïns determinen si cada espècie sobreviu o es perd.
Els científics que intenten aprendre sistemes dinàmics elaboren còpies simplificades o models (corregides mitjançant equacions matemàtiques) i tracten de fer funcionar aproximadament com un sistema real. Introdueixen el model en l'ordinador i veuen com evoluciona al llarg del temps i en quina mesura canvia canviant els paràmetres.
Per exemple, el sistema ecològic pot incloure climes diferents, nombre d'habitants, índex de natalitat, aliments diaris necessaris, comportament animal, etc. El model pot acabar amb la pèrdua d'una espècie, quan hi ha massa menjar pobre o presa, o quan hi ha equilibri entre espècies. Tot depèn de la introducció dels paràmetres.
A vegades, els analistes del sistema analitzen l'estat final d'un sistema i intenten reconstruir-lo per a investigar les causes que van portar al sistema a aquesta situació. Un exemple cèlebre ha estat el següent: en la civilització maia VIII. Un model per a explicar el col·lapse ocorregut en el segle XX.

El modern estudi del caos va començar en la dècada dels 60 amb un inconvenient descobriment: un conjunt d'equacions matemàtiques d'aparença simple, capaç de descriure sistemes dinàmics creats per condicions de comportament rígid i inicials. Les petites diferències en la situació inicial generen grans diferències en l'evolució del sistema. A això se li ha anomenat efecte papallona. Aquesta paraula (al mig broma) indica que el moviment de les ales d'una papallona, realitzat aquí i ara, influeix en la climatologia de Pequín del mes següent.
En la dècada dels 70, un grup de científics va treballar per a obrir camí en el regne del desordre. Eren matemàtics, físics, biòlegs, sociòlegs, economistes i fisiòlegs. Buscaven explicacions sobre la irregularitat que veien en els seus treballs, utilitzant un nou sistema d'anàlisi.

Vint anys després, el terme caos s'ha convertit en una descripció detallada d'una tendència (moviment científic). Augment de conferències, programes de recerca i publicacions. Botant sobre una taula van sortir uns articles sobre l'estranya dinàmica d'una pilota, juntament amb uns altres sobre mecànica quàntica.
La ciència del desordre ha creat unes tècniques basades en l'ús d'ordinadors. Aquestes tècniques ofereixen imatges del caos, estructures fascinants, hipnòtiques, delicades i de dificultat infinita.
En realitat, els models matemàtics que tracten de mostrar un sistema ecològic, climatològic, econòmic o altres sistemes de gran dificultat, estan formats per milers d'equacions i requereixen molt temps de processament per ordinador.

No obstant això, existeixen alguns models que es formulen amb poques relacions i que tenen una gran dificultat.
Un model matemàtic simple pot partir-se d'un valor inicial al qual denominarem de principi i, després d'uns càlculs, crear un valor final: D'acabat. Aquest últim valor s'introdueix en el model com a valor inicial i així successivament. La reintroducció de la sortida com a entrada es denomina realimentación. Hi ha realimentación, per exemple, quan un micròfon pren la sortida de l'amplificador. Al final, l'efecte
és insostenible.
Inicial = 1,1
i calculem el seu quadrat. Es calcula novament el quadrat del valor del Xbucal obtingut, etc. La seqüència de números obtinguts serà la següent: 1,21; 1,4641; 2,14358881;...
Continueu traient els comptes. Però lentament els números són cada vegada més
grans, sense límits.
Inicial = 0,99
amb la següent seqüència: 0,9801; 0,96059601; 0,922744694; ... Lentament, però aquesta successió s'acosta a zero. Sorprèn que els números tan pròxims entre si (1,1 i 0,99) tinguin un comportament tan
diferent.
D'acabat = (d'inici)2.
S'ha utilitzat la norma. També podem utilitzar altres fórmules que se'ns ocorrin i veure el comportament. Per exemple:
D'acabat = R.Xinicio (1 - D'inici).

relació, on R és qualsevol número que es tria al principi. Aquesta fórmula es diu equació logística i era una de les primeres que s'estudiaven.
En lloc d'intentar interpretar la successió de números que s'obté, es pot reproduir gràficament. En l'eix horitzontal situarem els valors de R, per exemple entre 2 i 5. En l'eix vertical per al punt inicial
(Inicial = 0,6, p. ex.)
Situarem la successió dels valors obtinguts. La figura 1 mostra la representació gràfica del resultat. Apareixen branques que se separen fins a l'infinit.
Atractor de Lorenz

En 1963, Edwarz Lorenz estava analitzant els remolins que es produeixen per escalfament i refredament de les capes atmosfèriques. El fenomen modelizado mitjançant un sistema d'equacions, que semblava senzill, va representar gràficament el recorregut de la partícula que es deixa dins d'un remolí.
La imatge obtinguda, avui clàssica, va donar a conèixer la difícil estructura oculta en les equacions i es va convertir en la bandera dels primers examinadors del caos. En la figura 2 es mostra l'atracció de Lorenz.
Com a meteoròleg, Lorenz va publicar el seu descobriment en la revista “Journal of the Atmospheric Sciences”, lluny de les mans de físics, biòlegs i enginyers.
Fractals

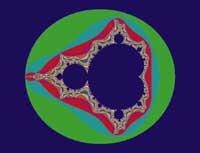
Benoit Mandelbrot, matemàtic investigador que va treballar en l'empresa IBM, va inventar un nou element que més tard va dir fractal.
Mandelbrot va veure una imatge coneguda en diferents llocs: a l'altura dels preus de les mercaderies, va sorprendre els enginyers en problemes de sorolls en les línies telefòniques, etc. En tots ells es veia la mateixa característica, una signatura que denunciava el caos. Quan s'analitzaven més detalladament, les regles de l'evolució eren cada vegada més difícils.
Els artistes troben la bellesa ideal en imatges clàssiques com a línies, plans i esferes, una estructura harmoniosa. No obstant això, la realitat mostra una geometria complexa, trencada i barrejada. Descontinuidades, sorolls de sobte i comportaments estranys van ser descrits per Mandelbrot mitjançant conceptes matemàtics abstractes. El fractal ens dóna una via per a modelar aquesta complexa realitat.

Les corbes fractals poden generar-se per mitjà d'un ordinador i tenen unes formes fascinants, com es mostra en les Figures 3-10. Corals, galàxies i dracs fractals representen criatures tan complexes com les que ens envolten.
La figura 11 mostra una imatge del planeta Acua-Tor. És un planeta en forma de toroides la superfície marina de la qual està coberta per un plasma fractal. Si el lector es fixa en ell, veurà aviat algunes espècies que lluiten per sobreviure en Acua-Torre.





