Imaxinaría?
Por exemplo, si o que queremos representar é un corpo xeométrico, utilizaremos a técnica da perspectiva. Si pola contra o corpo é a cara dunha persoa, por exemplo, a técnica das sombras. Por suposto, ambas se poden utilizar simultaneamente.

En canto á perspectiva, podemos dicir que ademais de ser una rama da Xeometría, é una ferramenta moi útil paira os artistas. E é que tanto os científicos como os artistas visitaron o XV. Acéptase o que introduciron no século XIX, e científicos e artistas escribiron numerosos libros sobre perspectiva. Entre os artistas que utilizaron a técnica da perspectiva destacan Filippo Brunelleschi, Piero della Francesca (autor do libro De perspectiva pingendi, entre outros), Leon Battista Alberti (autor do libro De pictura neste libro, que escribiu un resumo de todos os descubrimentos de entón sobre a Xeometría aplicada á imaxe e a pintura), escribimos no Tratado da pintura horizontal (Adenda da pintura).
Científicos: O tradutor Federico Commandino (en 1558 publicou una obra sobre a perspectiva), Daniele Barbarbaro (autor do libro A práctica da perspectiva ... obra moi útil a pintores, escultores e arquitectos), o arquitecto Jacopo Barozzi (autor do libro As dúas regras da perspectiva práctica), autor do libro Carribiolo, publicado en 1583. Nel aparece por primeira vez o seguinte teorema: trátase dun conxunto de perspectivas rectas e converxentes dun fai de rectas paralelas. En leste libro a área de perspectiva alcanzou o nivel científico).
É comprensible este espazo, os pintores de entón (XIV. e XV. se pensamos que trataban de estudar as bases científicas da súa arte (séculos XVI). Uno dos maiores problemas que presentaban os artistas era a representación de rectas paralelas, que se resolveron con perspectiva.
Pero deixando a historia volvemos ao noso tema. Agora si, podemos dicir que todo o tridimensional pódese representar nunha páxina. Se resolvemos este problema, demos a volta e vexamos que podemos responder á seguinte pregunta: Todas as imaxes bidimensionales representan un ser tridimensional?
Paira presentar esta resposta só tes que mirar as tres primeiras imaxes.

Na primeira imaxe tápase cun papel, primeiro a parte inferior (por baixo do centro) e logo a parte superior. Se o fas, descubrirás como combinando imaxes de dúas cousas tridimensionales pódese conseguir una imaxe imposible, que non se pode materializar en tres dimensións. O autor desta imaxe é Roger Hayward e o seu título é un monumento indicible. Non podemos dicir que a perspectiva xogue un papel importante neste efecto. Con todo, na parte superior utilízase a perspectiva e na parte inferior a sombra paira representar as tres dimensións.
Na segunda e terceira figura, a perspectiva xoga un papel importante, pero non como se podía esperar, é dicir, paira representar cousas que realmente existen, senón paira expresar seres imposibles. Sorprendente! O que foi a invención de Cristo, agora convértese nun rival e parece que só nos vai a producir quebradizos de cabeza. Con todo, non debemos pensar así. As imaxes non perden o seu adorno. Pola contra, gañan beleza, encanto, fascinación e misticismo.
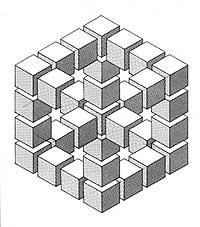
A segunda, aínda que imposible, é distinta. Nesta imaxe obtense a representación óptica mediante a perspectiva. A primeira vista parece que a imaxe é real, é dicir, que se pode materializar en tres dimensións. Son só cubos. Pero si miras ben e seguindo as liñas de cubo por diferentes camiños, darasche conta de que un cubo dun vértice ten que estar á vez á altura e debaixo do cubo do outro vértice. Isto dinos que é imposible.
Este tipo de figuras imposibles converteunas en arte. C. Escher. Podes volver ver outro cadro aquí. Xa aparecían nos números 3 e 5. Nesta terceira imaxe tes un traballo titulado A relatividad. Escher naceu na localidade holandesa de Leeawarden en 1898 e estudou na Escola de Arquitectura e Deseño Decorativo de Harlem. O seu tipo de arte foi denominado arte matemática. E é que, como dixo o propio Escher: "moitas veces atópome máis preto dos matemáticos que dos artistas". A súa frase é: "todos os meus traballos son xogos. Xogos serios". E iso é precisamente o que se ve na terceira figura, o xogo de escaleiras.

Outro tipo de imaxes son aquelas que ocultan dúas imaxes. Traémosche:
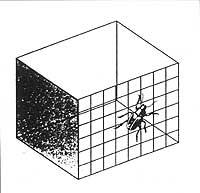
No cuarto temos un prisma cadrado e un escaravello (idea de introducir o escaravello L.S. Penrose e R. Penrose foi pai e fillo). Onde ves o escaravello dentro ou fóra do prisma? Paira conseguir ambos os efectos debes mirar ao prisma (non ao escarzano) e achegar un vértice interno (é dicir, supor que está máis cerca) ou afastalo (é dicir, supor que está máis lonxe) como queiras. Este efecto é tamén a influencia da perspectiva.

A quinta imaxe corresponde á bandeira canadense, coa folla de arce na parte branca central. Pero se o miras con moito coidado tamén podes ver a dúas persoas falando. Téntao.
No sexto, a moza anciá de Boring, coñecida pola súa idade. Nesta imaxe moita xente ve a un mozo fascinante e outros moitos a unha tolemia fea. Que ves ti? A resposta permite dar interpretacións diferentes sobre a túa identidade. Pero iso é obra doutros e non de nós.

Outra representación paira terminar. Ao final desta páxina tes un cravo na figura 7. Deixar a revista sobre a mesa, á altura dun bordo. Se miras de arriba a abaixo os cravos, veralos tombados na páxina. Agora flexiona lixeiramente e coloca un ollo (pechar o outro) no punto que apuntan os cravos aproximadamente e mira os cravos a niveis. Nesta posición parecerache que os cravos están cravados na folla. Non é así?





