Imatgeria?
Per exemple, si el que volem representar és un cos geomètric, utilitzarem la tècnica de la perspectiva. Si per contra el cos és la cara d'una persona, per exemple, la tècnica de les ombres. Per descomptat, ambdues es poden utilitzar simultàniament.

Quant a la perspectiva, podem dir que a més de ser una branca de la Geometria, és una eina molt útil per als artistes. I és que tant els científics com els artistes han visitat el XV. S'accepta el que van introduir en el segle XIX, i científics i artistes van escriure nombrosos llibres sobre perspectiva. Entre els artistes que van utilitzar la tècnica de la perspectiva destaquen Filippo Brunelleschi, Piero della Francesca (autor del llibre De perspectiva pingendi, entre altres), Leon Battista Alberti (autor del llibre De pictura en aquest llibre, que va escriure un resum de tots els descobriments de llavors sobre la Geometria aplicada a la imatge i la pintura), escrivim en el Tractat de la pintura horitzontal (Addenda de la pintura).
Científics: El traductor Federico Commandino (en 1558 va publicar una obra sobre la perspectiva), Daniele Barbarbaro (autor del llibre La pràctica de la perspectiva ... obra molt útil a pintors, escultors i arquitectes), l'arquitecte Jacopo Barozzi (autor del llibre Les dues regles de la perspectiva pràctica), autor del llibre Carribiolo, publicat en 1583. En ell apareix per primera vegada el següent teorema: es tracta d'un conjunt de perspectives rectes i convergents d'un feix de rectes paral·leles. En aquest llibre l'àrea de perspectiva va aconseguir el nivell científic).
És comprensible aquest espai, els pintors de llavors (XIV. i XV. si pensem que tractaven d'estudiar les bases científiques del seu art (segles XVI). Un dels majors problemes que presentaven els artistes era la representació de rectes paral·leles, que es van resoldre amb perspectiva.
Però deixant la història tornem al nostre tema. Ara sí, podem dir que tot el tridimensional es pot representar en una pàgina. Si resolem aquest problema, donem la volta i vegem què podem respondre a la següent pregunta: Totes les imatges bidimensionals representen un ser tridimensional?
Per a presentar aquesta resposta només has de mirar les tres primeres imatges.

En la primera imatge es tapa amb un paper, primer la part inferior (per sota del centre) i després la part superior. Si ho fas, descobriràs com combinant imatges de dues coses tridimensionals es pot aconseguir una imatge impossible, que no es pot materialitzar en tres dimensions. L'autor d'aquesta imatge és Roger Hayward i el seu títol és un monument indicible. No podem dir que la perspectiva jugui un paper important en aquest efecte. No obstant això, en la part superior s'utilitza la perspectiva i en la part inferior l'ombra per a representar les tres dimensions.
En la segona i tercera figura, la perspectiva juga un paper important, però no com es podia esperar, és a dir, per a representar coses que realment existeixen, sinó per a expressar éssers impossibles. Sorprenent! El que va ser la invenció de Crist, ara es converteix en un rival i sembla que només ens produirà maldecaps. No obstant això, no hem de pensar així. Les imatges no perden el seu adorn. Per contra, guanyen bellesa, encant, fascinació i misticisme.
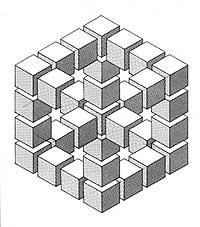
La segona, encara que impossible, és diferent. En aquesta imatge s'obté la representació òptica mitjançant la perspectiva. A primera vista sembla que la imatge és real, és a dir, que es pot materialitzar en tres dimensions. Són només galledes. Però si mires bé i seguint les línies de cub per diferents camins, t'adonaràs que un cub d'un vèrtex ha d'estar alhora a l'altura i sota el cub de l'altre vèrtex. Això ens diu que és impossible.
Aquest tipus de figures impossibles les va convertir en art. C. Escher. Pots tornar a veure un altre quadre aquí. Ja apareixien en els números 3 i 5. En aquesta tercera imatge tens un treball titulat La relativitat. Escher va néixer en la localitat holandesa de Leeawarden en 1898 i ha estudiat a l'Escola d'Arquitectura i Disseny Decoratiu d'Harlem. El seu tipus d'art ha estat denominat art matemàtic. I és que, com ha dit el propi Escher: "moltes vegades em trobo més prop dels matemàtics que dels artistes". La seva frase és: "tots els meus treballs són jocs. Jocs seriosos". I això és precisament el que es veu en la tercera figura, el joc d'escales.

Un altre tipus d'imatges són aquelles que oculten dues imatges. Et portem:
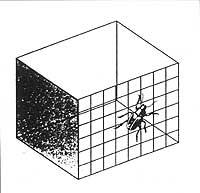
En el quart tenim un prisma quadrat i un escarabat (idea d'introduir l'escarabat L.S. Penrose i R. Penrose va ser pare i fill). On veus l'escarabat dins o fora del prisma? Per a aconseguir tots dos efectes has de mirar al prisma (no a l'escarser) i acostar un vèrtex intern (és a dir, suposar que està més a prop) o allunyar-ho (és a dir, suposar que està més lluny) com vulguis. Aquest efecte és també la influència de la perspectiva.

La cinquena imatge correspon a la bandera canadenca, amb la fulla d'auró en la part blanca central. Però si ho mires amb molta cura també pots veure a dues persones parlant. Intenta-ho.
En el sisè, la jove anciana de Boring, coneguda per la seva edat. En aquesta imatge molta gent veu a un jove fascinant i molts altres a una bogeria lletja. Què veus tu? La resposta permet donar interpretacions diferents sobre la teva identitat. Però això és obra d'uns altres i no de nosaltres.

Una altra representació per a acabar. Al final d'aquesta pàgina tens un clau en la figura 7. Deixar la revista sobre la taula, a l'altura d'una vora. Si mires de dalt a baix els claus, els veuràs tombats en la pàgina. Ara flexiona lleugerament i col·loca un ull (tancar l'altre) en el punt que apunten els claus aproximadament i mira els claus a ras. En aquesta posició et semblarà que els claus estan clavats en la fulla. No és així?





