Infini Infini
L'infini est difficile à définir et toutes les définitions auront des arguments pour et contre. Si nous nous adressons à un vocabulaire commun, il est défini comme celui qui n'a pas de fin et ne peut être indéfini. La définition est détaillée et semble raisonnable. L'intuition va aussi là-bas, mais maintenant nous nous demandons, y a-t-il quelque chose qui n'a pas de limites ? S'il n'y avait rien sans limites, nous ne définirons rien. Il faut donc chercher quelque chose sans limites.
La première idée qui vient à l'esprit est l'univers, car il est le plus grand que nous connaissons. Cependant, il y a 2000 ans Archimède a prouvé que l'univers était également fini quand il a calculé le nombre de grains de sable nécessaires pour remplir l'univers, moins de 1063. Malgré sa grande quantité, il est fini. Souvent, les êtres humains mélangent infini et de grandes choses. Beaucoup de choses sont grandes mais ont des limites. Par conséquent, ils ne sont pas infinis.
Cela épuise toutes les possibilités existantes dans le monde réel/physique. Nous devons donc aller dans le monde de l'imagination. Dans le monde de l'imagination, nous trouvons les plus grands obstacles à la compréhension de l'infini, car le monde de l'imagination est vaste et sans limites. D'autre part, chacun a sa propre imagination et pour nous comprendre avec un autre ami, le monde des illusions que j'avais doit unir.
Archimède lui-même nous a donné l'idée de trouver quelque chose sans limites. Il a calculé la quantité de grains de sable nécessaires pour remplir l'univers. Ce nombre de grains, 1063, était un nombre normal fini. Mais les chiffres que nous utilisons pour compter sont-ils finis ? Non, bien sûr. Il est un peu illimité, l'ensemble des nombres naturels,
N = {1, 2, 3, 4, 5, ..., 1.000.000, 1.000.001, ..., 1063, ...}.
Si on ajoute aux nombres naturels les opposés, les négatifs et les 0 on obtient des nombres entiers, qui sont aussi infinis :
Z ={...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}.
L'ensemble des nombres entiers est la partie de l'ensemble des nombres rationnels. Par conséquent, les nombres rationnels sont également infinis:
Q = précédents..., -3, -1/3, -1/2, -2, -1, 0, 1, 2, 1/2, 1/3, 3, ...}.
Enfin, en ajoutant irrationnellement aux nombres rationnels (…, p…) nous obtiendrons des nombres réels qui sont aussi infinis. Par conséquent, nous avons élaboré une chaîne comme suit:
N C Z C Q C R.
Tous les ensembles sont infinits.Lorsque nous
comptons les éléments des ensembles finis, l'application bijetive est définie entre l'ensemble et un sous-ensemble du groupe N. Par exemple, ensemble de voyelles = {a, e, i, o, u}. Combien d'éléments avez-vous?
à -1, e -2, i -3, ou -4, u -5
Par conséquent, entre les groupes {a, e, i, o, u} et {1, 2, 3, 4, 5} nous avons défini une application bijetive.Les groupes finis ont différents éléments :
l'ensemble des voyelles 5 éléments, l'ensemble des consonnes 21 éléments. Que se passera-t-il avec les ensembles infinis ?
Pour savoir combien d'éléments il y a dans le groupe Z plus que dans le groupe N nous utiliserons l'hôtel infini, l'hôtel N. Supposons un hôtel avec des chambres infinies (1er, 2ème, 3ème, …) toutes les chambres sont pleines. En raison d'une mauvaise communication, un groupe d'amis infinis avance un jour et les responsables de l'hôtel doivent leur fournir une chambre pour la corriger. Comment introduiront-ils les nouveaux amis infinis (-1, -2, -3, ...) dans chaque chambre les responsables de l'hôtel?
Une solution peut être: (-1) mettre le nouvel ami dans la chambre 1, mettre le compagnon de la chambre 1 (1) dans la chambre 2, mettre le compagnon de la chambre 2 (2) dans la chambre 3 et ainsi de suite avec les autres. Nous avons adapté votre chambre au premier ami. Nous allons maintenant placer (-2) le deuxième ami. Nous introduisons le compagnon (-2) dans la chambre 1, nous passons au compagnon (-1) dans la chambre 1 à la chambre 2. Ami 2ème (1) chambre à 3ème et ainsi avec les autres. En général, pour introduire un nouvel ami, à commencer par la première chambre, les personnes qui se trouvent dans les chambres passeront aux chambres suivantes et laisseront le premier vide.
Au dernier moment (0), de nouveaux amis sont venus chercher un site. En suivant la procédure ci-dessus, nous vidons la 1ère chambre pour y accéder.
Ainsi, à l'Hôtel N il y avait des amis 1, 2, 3, ... et nous avons inclus -1, -2, -3, ... et 0 personnes, en adaptant chacun d'eux dans une chambre. Par conséquent, nous pouvons dire qu'il y a autant de personnes que de chambres. Autrement dit, ils ont autant d'éléments que les groupes Z et N.
| Chambres et suites Chambres |
1. | 2. | 3. | 4ème | 5. | ... |
Hôtel complet |
1. | Services | Services | Sécurité et sécurité | Services | ... |
Entrez un nouvel ami |
-1 | 1. | Services | Services | Sécurité et sécurité | ... |
Ajouter un nouvel ami 2 |
-2 | -1 | 1. | Services | Services | ... |
Un autre jour, nous avons retrouvé l'hôtel N plein. Mais à midi infinies personnes ont quitté l'hôtel. Chers amis, 4ème, 6ème, … étaient dans les chambres. Par conséquent, la moitié des chambres ont été vides. Dans l'après-midi est venu un autre groupe infini (1,2,3, ...). Les responsables de l'hôtel n'ont pas eu de problèmes pour s'adapter aux chambres vides. (1) mettre le compagnon dans la chambre 2, (2) le compagnon dans la chambre 4, (3) l'ami dans la chambre 6 et ainsi de suite avec les autres.
| Chambres et suites Chambres |
1. | 2. | 3. | 4ème | 5. | 6ème | ... |
Hôtel complet |
a) a) | b) | c) c) | d) d) | e) e | f) f) | ... |
Demi-hôtel vide |
a) a) | c) c) | e) e | ... | |||
Hôtel à nouveau rempli |
a) a) | 1. | c) c) | Services | e) e | Services | ... |
Nous pouvons dire que dans le centre des chambres nous avons mis autant de personnes que dans tout l'hôtel. En d'autres termes, un ensemble infini (1,2,3,...) peut avoir autant d'éléments que de sous-ensembles infinis (2,4,6,...).
Le groupe suivant est Q, les nombres rationnels sont cohérents entre deux nombres entiers, sans que le diviseur soit 0. Les rapports pour compter les nombres du groupe Q seront considérés comme un nombre unique. Comme dans le cas précédent, nous démontrerons que dans le groupe Q il y a autant de nombres que dans le groupe N par une application bijetive. Cette application sera fournie par une table dans laquelle seuls les nombres positifs apparaîtront, mais les nombres négatifs seront comptabilisés de la même manière.
Les nombres indiquant les fractions entre parenthèses sont déjà apparus. C'est pourquoi ils ne sont pas calculés dans la table inférieure.
1349101827…281626…5715192939…6142538…11132024374353…123652…21233035445168…22345067…....................................A partir de ce tableau, on peut vérifier que pour chaque élément du groupe N il y a un élément du groupe Q et par contre, pour chaque élément du groupe Q il y a un élément du groupe N. En bref, on peut démontrer que l'application est un bijectif.
Tous ces ensembles infinis semblent avoir le même nombre d'éléments, A1. Dans le groupe suivant, R, en plus des nombres raisonnables, sont inclus les nombres irrationnels. Combien sont les nombres irrationnels ? Avant de compter tous les nombres réels nous compterons ceux compris entre 0 et 1.
Nous vérifions que dans l'intervalle (0,1) il y a plus de nombres que dans le groupe N. L'idée de la démonstration est: Nous supposons qu'entre les groupes N et (0,1) l'application bijetive est définie et nous verrons qu'un nombre situé entre 0 et 1 n'a pas d'image dans le groupe N. Par conséquent, nous concluons qu'il n'est pas possible de définir ce type d'applications. d'où il est déduit que dans le groupe (0,1) il y a plus d'éléments que dans le groupe N. Ce plus grand nombre d'éléments sera appelé c et sera conforme à A1. Nous allons expliquer la démonstration.
Si l'application bijetive était définie entre les groupes N et (0,1), nous pourrions écrire la correspondance suivante:
Nombres normaux (0,1)alternatifs intercales10,a1a2a3a4a5 ...20,b1b2b3b4b5 ...30,c1c2c3c4c5 ....40,d1d3d4d5 ....50,e1e2e3e4e5 ...........
A gauche tous les nombres naturels et à droite, en forme décimale, tous les éléments du groupe (0,1). Prenons les numéros suivants:
z1a1, z2b2, z3c3, z4d4, z5e5,...
et compléter le numéro décimal suivant:
0,z1z2z3z4z5...
Ce nombre est compris entre 0 et 1 et n'est pas le même que ceux qui apparaissent à droite parce que nous avons choisi (z1a1, z2b2, z3c3, z4d4, z5e5, ...). Par conséquent, aucun élément du groupe N situé à gauche ne correspond. Dans le groupe (0,1) il y a plus d'éléments que dans le groupe N.
La plage (0,1) est seulement une petite partie de l'ensemble R, mais a plus d'éléments que l'ensemble N. Comparons maintenant les groupes (0,1) et R. La comparaison sera faite par une figure géométrique.
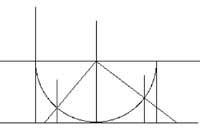
Sur l'axe OX des coordonnées du plan se situe l'intervalle (0,1). (1/2,1/2) on dessine une demi-circonférence supérieure avec centre et rayon 1/2. Du point x de l'intervalle (0,1) une verticale s'élève jusqu'à atteindre la moyenne circonférence. On dessine la droite qui passe par le centre de la circonférence et par le point précédent. Cette droite coupe l'axe OX au point et. et est le point correspondant à x. Il peut également être fait à l'envers. En prenant le point et´ du groupe R, on dessine la droite qui relie ce point au centre de la circonférence. Cette droite coupe la demi-circonférence en un point. De ce point bas, reliée à l'axe OX jusqu'à trouver l'axe OX au point x´. x´ correspond au point et´.
Ainsi, entre les groupes (0,1) et R une application bijetive a été définie. Cela signifie que les groupes (0,1) et R ont le même nombre d'éléments, c.
Tout comme le numéro 1 est le suivant 2 du nombre naturel, nous pouvons appeler A2 au suivant de l'infini A1 et A3 au suivant et ainsi de suite. Nous avons également trouvé l'infini c et nous avons montré que A1 c. La question qui nous vient maintenant à l'esprit est: Y a-t-il l'infini c A2 ? Est-ce que c = A2? Cette question est pour le moment en attente de réponse.
L'arithmétique des nombres finis est connue, tandis que celle des nombres infinis n'est pas. On pourrait démontrer que:
A1 + n = A1c + n = cA1 + A1 = A1c + A1 = cn . A1 = A1c + c = cA1 . A1 = A1n . c = c(A1)n = A1c . c = c(2)A1 = (A1)A1 = c(c)n = c(c)A1 = c(2)c = (c)c = (c)c = (c)c = autre infiniA1 N est le nombre d'éléments des ensembles Z et Q. c est le
nombre d'éléments de l'ensemble R. Dans tous les n
est le nombre normal.
Le résultat final signifie qu'il y a différents nombres infinis.





