Infinite
Infinity is difficult to define and all definitions will have arguments for and against. If we turn to a common vocabulary it is defined as one that has no end and cannot be indefinite. The definition is detailed and seems reasonable. Intuition also goes around, but now we wonder, is there something that has no limits? If there was nothing without limits, we would define nothing. Therefore, you have to look for something without limits.
The first idea that comes to mind is the universe, because it is the greatest thing we know. However, 2,000 years ago Archimedes showed that the universe was also finite when he calculated the number of grains of sand needed to fill the universe, less than 1063. Despite its large amount, it is finite. Many times humans mix infinity and great things. Many things are great but they have limits. Therefore, they are not infinite.
This exhausts all the possibilities existing in the real/physical world. Therefore, we have to go to the world of imagination. In the world of imagination we find the greatest obstacles to understanding the infinite, since the world of imagination is wide and without limits. On the other hand, everyone has their own imagination and to understand each other, the world of illusions that I had to unite.
Archimedes himself gave us the idea of finding something without limits. He calculated the amount of grains of sand needed to fill the universe. This number of grains, 1063, was a finite natural number. But are the numbers we use to count finite? No, of course. There is something unlimited, the set of natural numbers,
N = {1, 2, 3, 4, 5, .., 1.000.000, 1.000.001, .., 1063, ...}.
If we add opposites, negatives and 0 to the natural numbers we will get integers, which are also infinite:
Z ={..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ..}.
The set of integers is the part of the set of rational numbers. Therefore, rational numbers are also infinite:
Q = previous..., -3, -1/3, -1/2, -2, -1, 0, 1, 2, 1/2, 1/3, 3,...}.
Finally, adding irrational numbers to rational numbers (…, p,…) we will get real numbers that are also infinite. Therefore, we have developed a chain like the following:
N C Z C Q C R.
In it all sets are infinite. When
we count the elements of the finite sets, the bijective application between the set and a subset of group N is defined. For example, set of vowels = {a, e, i, o, u}. How many elements do you have?
to -1, e -2, i -3, or -4, u -5
Therefore, between groups {a, e, i, o, u} and {1, 2, 3, 4, 5} we have defined a bijective application.Finite groups have different elements: the set of 5
elements vowels, the set of consonants 21 elements. What will happen to infinite sets?
To know how many elements there are in Group Z more than in Group N we will use the infinite hotel, Hotel N. Suppose a hotel with infinite rooms (1º, 2º, 3º, …) all rooms are full. Due to poor communication, a group of infinite friends comes forward one day and hotel managers must provide them with a room to correct it. How will the new infinite friends (-1, -2, -3, ..) introduce into each room the hotel managers?
One solution may be: (-1) put the new friend in room 1, put the roommate 1 (1) in room 2, put the roommate 2 (2) in room 3 and so with others. The first friend has adapted his room. Now we will place (-2) the second friend. We introduce the companion (-2) in room 1, we pass to the companion (-1) in room 1 to room 2. Friend of 2nd (1) room to 3rd and so with others. In general, to introduce a new friend, starting with the first room, people who are in the rooms will move to the next rooms and leave the first empty.
At the last moment (0) new friends have come to search for site. Following the above procedure, we will empty the 1st room to access it.
So, in Hotel N there were friends 1, 2, 3, ... and we have included -1, -2, -3, .. and 0 people, adapting each of them in a room. Consequently, we can say that there are as many people as there are rooms. That is, they have as many elements as groups Z and N.
| Rooms |
1. | 2. | 3. | 4th | 5. | ... |
Full hotel |
1. | Services | Services | Security | Services | ... |
Introduce a new friend |
-1 | 1. | Services | Services | Security | ... |
Add new friend 2 |
-2 | -1 | 1. | Services | Services | ... |
Another day we have found the hotel N full again. But at noon countless people have left the hotel. Dear friends, 4th, 6th, … were in the rooms. Therefore, half of the rooms have been empty. In the afternoon another infinite group came (1,2,3, ..). Hotel managers have had no problems adapting to empty rooms. (1) put the partner in room 2, (2) the partner in room 4, (3) the friend in room 6 and so on with others.
| Rooms |
1. | 2. | 3. | 4th | 5. | 6th | ... |
Full hotel |
a) | b) | c) | d) | e | f) | ... |
Half empty hotel |
a) | c) | e | ... | |||
Hotel full again |
a) | 1. | c) | Services | e | Services | ... |
We can say that in the center of the rooms we have put as many people as in the whole hotel. In other words, an infinite set (1,2,3,...) can have as many elements as infinite subsets (2,4,6,...).
The next group is Q, rational numbers are quotients between two integers, without the divisor being 0. Quotients for counting Group Q numbers will be considered as a unique number. As in the previous case, we will show that in group Q there are as many numbers as in group N through a bijective application. This application will be provided by a table in which only positive numbers will appear, but negative numbers will be counted in the same way.
Numbers indicating fractions in parentheses have already appeared. Therefore they are not computed in the table below.
1349101827…281626…5715192939…6142538…11132024374353…123652…21233035445168…22345067…................................From this table you can check that for each element of group N there is an element of group Q and on the contrary, for each element of group Q there is an element of group N. In short, it can be shown that the application is a bijective.
All these infinite sets seem to have the same number of elements, A1. In the next group, R, in addition to rational numbers, includes irrational numbers. How many are the irrational numbers? Before counting all real numbers we will count those between 0 and 1.
We check that in the range (0.1) there are more numbers than in group N. The idea of the demonstration is: We assume that between groups N and (0.1) the bijective application is defined and we will see that a number between 0 and 1 has no image in group N. Therefore, we will conclude that it is not possible to define such applications. from which it follows that in group (0.1) there are more elements than in group N. This greater number of elements will be called c and will be met with A1 < c. Let's explain the demonstration.
If between groups N and (0.1) the bijective application was defined, we could write the following correspondence:
Natural numbers (0,1)alternate intercalos10,a1a2a3a4a5 ...20,b1b2b3b3b4b5 ...30,c1c2c3c4c5 ....40,d1d3d4d5 ...50,e1e2e3e4e5 ............
To the left all the natural numbers and to the right, in decimal form, all the elements of the group (0.1). Take the following numbers:
z1a1, z2b2, z3c3, z4d4, z5e5,...
and complete the following decimal number:
The...
This number is between 0 and 1 and is not the same as those on the right because we have chosen it (z1a1, z2b2, z3c3, z4d4, z5e5, ..). Therefore, there is no element of group N on the left. In group (0.1) there are more elements than in group N.
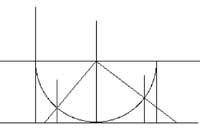
The range (0.1) is only a small part of the R set, but has more elements than the N set. Now compare groups (0.1) and R. The comparison will be made by a geometric figure.
In the OX axis of the plane coordinates is the range (0.1). (1/2.1/2) a superior semicircle with center and radius 1/2 is drawn. From point x of the interval (0.1) a vertical rises to reach the mean circumference. The line that passes through the center of the circumference and the previous point is drawn. This line will cut the OX axis at the point and. and is the point corresponding to x. It can also be done backwards. Taking the y´ point of group R, the line linking this point with the center of the circle is drawn. This line cuts the semicircle at one point. From this low point attached to the OX axis to find the OX axis at point x´. x´ corresponds to the point and´.
Thus, between groups (0.1) and R a bijective application has been defined. This means that groups (0.1) and R have the same number of elements, i.e. c.
Just as the number 1 is the next 2 of the natural number, we can call A2 to the next of infinity A1 and A3 to the next and so on. We have also found the infinite c and have shown that A1 < c. The question that comes to mind now is: Is there infinity c A2? That is, does c = A2 exist? This question is pending.
The arithmetic of finite numbers is known, while that of infinite numbers is not known. It could be shown that:
A1 + n = A1c + n = cA1 + A1 = A1c + A1 = cn . A1 = A1c + c = cA1 . A1 = A1n . c = c(A1)n = A1c . c = c(2)A1 = (A1)A1 = c(c)n = c(c)A1 = c(2)c = (c)c = (c)c = another infiniteA1 N is the number of elements of sets Z and Q. c is the
number of elements of set R. In all of them n
is the normal number.
The end result means that there are different infinite numbers.





