Infinit
L'infinit és difícil de definir i totes les definicions tindran arguments a favor i en contra. Si ens dirigim a un vocabulari comú es defineix com aquell que no té fi i no pot ser indefinit. La definició és detallada i sembla raonable. La intuïció també va per aquí, però ara ens preguntem hi ha alguna cosa que no té límits? Si no hi hagués res sense límits, no definiríem res. Per tant, cal buscar alguna cosa sense límits.
La primera idea que ve a la ment és l'univers, perquè és el més gran que coneixem. No obstant això, fa 2.000 anys Arquimedes va demostrar que l'univers era també finit quan va calcular el nombre de grans de sorra necessaris per a omplir l'univers, menys de 1063. Malgrat la seva gran quantitat, és finita. Moltes vegades els éssers humans barregem infinit i coses grans. Moltes coses són grans però tenen límits. Per tant, no són infinits.
Això esgota totes les possibilitats existents en el món real/físic. Per tant, hem d'anar al món de la imaginació. En el món de la imaginació trobem els majors obstacles per a comprendre l'infinit, ja que el món de la imaginació és ampli i sense límits. D'altra banda, cadascun té la seva pròpia imaginació i per a entendre'ns amb un altre amic, el món de les il·lusions que jo tenia ha d'unir.
El mateix Arquimedes ens va donar la idea de trobar alguna cosa sense límits. Ell va calcular la quantitat de grans de sorra necessaris per a omplir l'univers. Aquest nombre de grans, 1063, era un nombre natural finit. Però els números que utilitzem per a comptar són finits? No, clar. Aquí està una mica il·limitat, el conjunt dels nombres naturals,
N = {1, 2, 3, 4, 5, ..., 1.000.000, 1.000.001, ..., 1063, ...}.
Si afegim als nombres naturals els oposats, els negatius i els 0 obtindrem nombres enters, que també són infinits:
Z ={...., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}.
El conjunt de nombres enters és la part del conjunt de nombres racionals. Per tant, els nombres racionals també són infinits:
Q = anteriors..., -3, -1/3, -1/2, -2, -1, 0, 1, 2, 1/2, 1/3, 3, ...}.
Finalment, afegint irracionals als nombres racionals (…e,p,…) obtindrem nombres reals que també són infinits. Per tant, hem elaborat una cadena com la següent:
N C Z C Q C R.
En ell tots els conjunts són infinits.Quan
comptem els elements dels conjunts finits es defineix l'aplicació bijetiva entre el conjunt i un subconjunt del grup N. Per exemple, conjunt de vocals = {a, i, i, o, o}. Quants elements té?
a -1, e -2, i -3, o -4, o -5
Per tant, entre els grups {a, i, i, o, o} i {1, 2, 3, 4, 5} hem definit una aplicació bijetiva.Els grups finits
tenen diferents elements: el conjunt de vocals 5 elements, el conjunt de consonants 21 elements. Què passarà amb els conjunts infinits?
Per a saber quants elements hi ha en el grup Z més que en el grup N utilitzarem l'hotel infinit, l'hotel N. Suposem un hotel amb infinit habitacions (1r, 2n, 3r, …) totes les habitacions estan plenes. A causa d'una mala comunicació, un grup d'infinits amics s'avança un dia i els responsables de l'hotel han de proporcionar-los una habitació per a corregir-la. Com introduiran els nous infinits amics (-1, -2, -3, ...) en cada habitació els responsables de l'hotel?
Una solució pot ser: (-1) ficar al nou amic a l'habitació 1, ficar al company de l'habitació 1 (1) a l'habitació 2, ficar al company de l'habitació 2 (2) a l'habitació 3 i així amb els altres. Al primer amic li hem adaptat la seva habitació. Ara situarem (-2) al segon amic. Introduïm al company (-2) a l'habitació 1, passem al company (-1) a l'habitació 1 a l'habitació 2. Amic de 2n (1) habitació a 3r i així amb els altres. En general, per a introduir un nou amic, començant per la primera habitació, les persones que es trobin a les habitacions passaran a les següents habitacions i deixarem el primer buit.
En l'últim moment (0) han arribat nous amics a buscar lloc. Seguint el procediment anterior, buidarem la 1a habitació per a accedir a ella.
Així doncs, a l'Hotel N hi havia amics 1, 2, 3, ... i hem inclòs -1, -2, -3, ... i 0 persones, adaptant cadascun d'ells en una habitació. En conseqüència, podem dir que hi ha tantes persones com habitacions. És a dir, tenen tants elements com els grups Z i N.
| Habitacions |
1. | 2. | 3. | 4t | 5. | ... |
Hotel complet |
1. | Serveis | Serveis | Seguretat | Serveis | ... |
Introduir un nou amic |
-1 | 1. | Serveis | Serveis | Seguretat | ... |
Afegir nou amic 2 |
-2 | -1 | 1. | Serveis | Serveis | ... |
Un altre dia hem tornat a trobar l'hotel N ple. Però al migdia infinites persones han deixat l'hotel. Estimats amics, 4t, 6è, … eren a les habitacions. Per tant, la meitat de les habitacions han quedat buides. A la tarda ha vingut un altre grup infinit (1,2,3, ...). Els responsables de l'hotel no han tingut problemes per a adaptar-se a les habitacions buides. (1) ficar al company a l'habitació 2, (2) al company a l'habitació 4, (3) a l'amic a l'habitació 6 i així amb els altres.
| Habitacions |
1. | 2. | 3. | 4t | 5. | 6è | ... |
Hotel complet |
a) | b) | c) | d) | e | f) | ... |
Mig hotel buit |
a) | c) | e | ... | |||
Hotel de nou ple |
a) | 1. | c) | Serveis | e | Serveis | ... |
Podem dir que en el centre de les habitacions hem ficat tantes persones com en tot l'hotel. En altres paraules, un conjunt infinit (1,2,3,...) pot tenir tants elements com subconjunts infinits (2,4,6,...).
El següent grup és Q, els nombres racionals són quocients entre dos nombres enters, sense que el divisor sigui 0. Els quocients per a comptar els números del grup Q seran considerats com un número únic. Com en el cas anterior, demostrarem que en el grup Q hi ha tants números com en el grup N mitjançant una aplicació bijetiva. Aquesta aplicació la proporcionarem mitjançant una taula en la qual només apareixeran els números positius, però els números negatius es comptabilitzaran de la mateixa manera.
Els números que indiquen les fraccions entre parèntesis ja han aparegut. Per això no es computen en la taula inferior.
1349101827…281626…5715192939…6142538…11132024374353…123652…21233035445168…22345067…..........................A partir d'aquesta taula es pot comprovar que per cada element del grup N hi ha un element del grup Q i per contra, per cada element del grup Q hi ha un element del grup N. En definitiva, es pot demostrar que l'aplicació és un bijetivo.
Tots aquests infinits conjunts semblen tenir el mateix nombre d'elements, A1. En el grup següent, R, a més dels nombres racionals, s'inclouen els nombres irracionals. Quants són els nombres irracionals? Abans de comptar tots els nombres reals comptabilitzarem els compresos entre 0 i 1.
Comprovem que en l'interval (0,1) hi ha més números que en el grup N. La idea de la demostració és: Suposem que entre els grups N i (0,1) l'aplicació bijetiva està definida i veurem que un número situat entre 0 i 1 no té imatge en el grup N. Per tant, conclourem que no és possible definir aquest tipus d'aplicacions. d'on es dedueix que en el grup (0,1) hi ha més elements que en el grup N. Aquest major nombre d'elements es denominarà c i es complirà amb A1 < c. Explicarem la demostració.
Si entre els grups N i (0,1) estigués definida l'aplicació bijetiva, podríem escriure la següent correspondència:
Nombres naturals (0,1)alterns intercalos10,a1a2a3a4a5 ...20,b1b2b3b3b4b5 ...30,c1c2c3c4c5 ....40,d1d3d4d5 ....50,e1e2e3e4e5 ..........
A l'esquerra tots els nombres naturals i a la dreta, en forma decimal, tots els elements del grup (0,1). Prenguem els següents números:
z1a1, z2b2, z3c3, z4d4, z5e5,...
i completem el següent nombre decimal:
0,z1z2z3z4z5...
Aquest número està entre 0 i 1 i no és el mateix que els que apareixen a la dreta perquè així hem triat (z1a1, z2b2, z3c3, z4d4, z5e5, ...). Per tant, no correspon cap element del grup N situat a l'esquerra. En el grup (0,1) hi ha més elements que en el grup N.
El rang (0,1) és només una petita part del conjunt R, però té més elements que el conjunt N. Comparem ara els grups (0,1) i R. La comparació la realitzarem mitjançant una figura geomètrica.
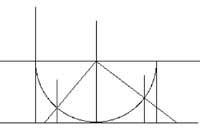
En l'eix OX de les coordenades del pla se situa l'interval (0,1). (1/2,1/2) es dibuixa una semicircumferència superior amb centre i radio 1/2. Des del punt x de l'interval (0,1) s'eleva una vertical fins a aconseguir la mitja circumferència. Es dibuixa la recta que passa pel centre de la circumferència i pel punt anterior. Aquesta recta tallarà l'eix OX en el punt i. i és el punt corresponent a x. També es pot fer a l'inrevés. Prenent el punt i´ del grup R, es dibuixa la recta que uneix aquest punt amb el centre de la circumferència. Aquesta recta curta la semicircumferència en un punt. Des d'aquest punt baixa unida a l'eix OX fins a trobar l'eix OX en el punt x´. x´ correspon al punt i´.
Així, entre els grups (0,1) i R s'ha definit una aplicació bijetiva. Això significa que els grups (0,1) i R tenen el mateix nombre d'elements, és a dir, c.
Igual que el número 1 és el següent 2 del nombre natural, podem cridar A2 al següent de l'infinit A1 i A3 al següent i així successivament. També hem trobat l'infinit c i hem demostrat que A1 < c. La pregunta que ens ve ara a la ment és: existeix l'infinit c A2? És a dir, existeix c = A2? Aquesta pregunta està de moment pendent de resposta.
L'aritmètica dels números finits és coneguda, mentre que la dels números infinits no. Es podria demostrar que:
A1 + n = A1c + n = cA1 + A1 = A1c + A1 = cn . A1 = A1c + c = cA1 . A1 = A1n . c = c(A1)n = A1c . c = c(2)A1 = (A1)A1 = c(c)n = c(c)A1 = c(2)c = (c)c = (c)c = un altre infinitA1 N és el nombre d'elements dels conjunts Z i Q. c és el
nombre d'elements del conjunt R. En tots ells n
és el número normal.
El resultat final significa que hi ha diferents números infinits.





