Théories d'auteurs Kaluza/i coupable et Klein/i, un monde de onze dimensions

Deux des quatre forces de base que nous avons pour définir la matière ont été réunies expérimentalement (électromagnétique et faible). Pour unifier la force violente, on a créé les Théories de l'Union Majeure (toujours sans démontrer expérimentalement). Mais les physiciens théoriques cherchent une théorie superlarge pour unir les quatre forces dans un cadre théorique. Pour cela, les soi-disant modèles de supersymétrie ont été créés, en adaptant les théories générales de la supergravitation. Cependant, la théorie supergravitationnelle N=8 est la plus adaptée à la réalité physique. Selon cette théorie, l'espace et le temps doivent être quantifiés et variables sur des distances supercourtes.

1.- Modèle et gravitation de Kaluza

À distance, le câble ressemble à une ligne courbe. Plus près, cependant, nous voyons que le point P est un cercle. Il est possible que dans l'espace de la tridimension ce que nous considérons normalement comme un point soit un petit cercle autour d'une autre dimension spatiale. C'est l'idée fondamentale de Kaluza et Klein dans la théorie unificatrice des forces électromagnétiques et gravitationnelles.

L'ancien rêve d'Einstein (unir le champ gravitationnel et électromagnétique avec la description géométrique) a été réinventé par le physicien polonais Theordor Kaluza et vers 1921 a essayé d'exprimer par géométrie la théorie électromagnétique de Maxwell. Mais pour mener à bien ce projet, il était nécessaire de remodeler sa géométrie afin que l'électromagnétique soit moulée dans cette géométrie.

Pour ce faire, Kaluza a postulé une dimension spatiale supplémentaire, de sorte que la géométrie qui dépend de la nature aurait quatre dimensions spatiales et un temps. La gravitation dans ce monde à cinq dimensions serait le résultat de la somme de la gravité normale et du champ électromagnétique de Maxwell. Si nous pouvions élargir notre perception en cinq dimensions, nous nous retrouverions avec un seul champ de force : le gravitationnel. Selon cette théorie, l'onde électromagnétique serait l'ondulation de la cinquième dimension.

La théorie de Kaluza a obtenu un grand succès mathématique. Mais il avait aussi une queue insurmontable. Autrement dit, si l'univers spatial est en quatre dimensions, pourquoi ne peut-on pas saisir physiquement la quatrième dimension ? Cette quatrième dimension ne sera-t-elle qu'une mythe mathématique ?

2.- Structure pentadimensional de Klein

En 1926, le physicien suédois Oscar Klein a essayé de démontrer la compatibilité de la structure pentadimensional et mécanique quantique de Kaluza. Pour ce faire, il a fourni une nouvelle version de l'équation de Schrödinger adapté aux cinq dimensions. Pour Klein, la quatrième dimension spatiale a une existence réelle.

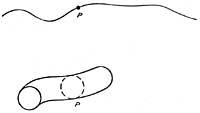
Pour mieux comprendre cela, supposons une ligne et un cercle associés à chaque point de cette ligne. L'union de la ligne d'une dimension avec le cercle d'une dimension crée un cylindre à deux dimensions. Supposons aussi un plan où tous les points de ce plan sont adaptés à un cercle, alors l'union entre le plan bidimensionnel et le cercle d'une dimension créera un en trois dimensions continues.

Avec le même raisonnement, on peut deviner qu'à chaque point on ajoute un continuum tridimensionnel et un cercle, qui sont bouclés dans la quatrième dimension. Ces boucles ne riraient pas dans l'espace, car elles ne sont pas dans l'espace. Ce que font ces spirales est d'élargir l'espace.

Klein a commencé le calcul des circonférences de ces cercles qui créent un univers de cinq dimensions. Pour cela, il a pris en compte les charges d'électrons et d'autres particules, comme les forces gravitationnelles entre elles. En cas de calcul, il a indiqué que la longueur de ces cercles serait comprise entre 10 et 30 cm.

Son petit chiffre nous indique pourquoi la cinquième dimension ne peut pas être perçue correctement. Ce chiffre est si petit qu'en plus d'un être vivant, aucun atome ne pourrait se déplacer dans ces dimensions.

Cette dimension est située à l'intérieur de l'atome. Pour détecter une structure aussi subtile, nous devrions avoir un accélérateur de fractions de plusieurs années de lumière.

3.- Généralisation de modèles de Kaluza-Klein : un monde de onze dimensions

Le modèle de Kaluza/Klein a été oublié pendant plusieurs années. Cependant, au cours des dernières années a surgi la passion de ce modèle parmi les scientifiques, mais maintenant dans un contexte différent: C'est-à-dire, dans le contexte des Théories de Major Union et des Théories Supergravitationnelles.

Dans le but d'unir les forces de la nature, dans une théorie, sept dimensions inconnues de l'Univers ont été proposées. Elle peut être exprimée comme une petite structure compacte, comme si chaque point de la sphère avait à chaque moment une sphère attachée. Les sphères situées à l'intersection des lignes de coordonnées sont des dimensions supplémentaires regroupées postulées dans la nouvelle théorie. Les sphères sont tangentes à chaque point par rapport au plan. En outre, la sphère et le plan ne génèrent que quatre dimensions et non 11 de la théorie. Les quatre dimensions sont les quatre coordonnées qui définissent un point.

La théorie de Kaluza/Klein a été réintégrée dans le domaine de la physique, en supposant que la symétrie des champs de force est le résultat d'une structure géométrique interne dans la nature. De plus, les symétries gauge sont des formes de géométrie ajoutées aux nouvelles dimensions spatiales.

Les problèmes que devrait couvrir la théorie généralisée de Kaluza/Klein sont les trois suivants. Vous devrez d'abord remplir un champ fermonique pour indiquer les fermions dans notre univers. Il devrait également indiquer au moins un champ bosonique et, bien sûr, le champ gravitationnel (origine des dimensions spirales cachées). Le modèle qui répond à toutes ces exigences est une version de la supergravité 11. La théorie moderne de Kaluza/Klein postule donc un univers de 11 dimensions. Sept de ces onze dimensions seraient enroulées à un niveau où elles seraient cachées pour l'observation directe.

Les dimensions dans lesquelles elles sont enroulées correspondent à un grand nombre de types de topologies, il faut donc effectuer un processus concret pour choisir la plus appropriée:

    Résoudre les équations de supergravité. Certaines de ces mesures pourraient correspondre à quatre dimensions spatio-temporelles et à une forme topologique fermée de sept dimensions. Ensuite, nous étudierons l'ensemble des symétries de chaque surface correspondant à la résolution des équations. L'ensemble des symétries nous définit la théorie non-abéline gauge qui doit se joindre à la gravité. Les différentes surfaces fermées présentent différents types de symétries, chacune définissant une théorie différente des Grandes Unions.
  1. Enfin, les structures d'ondes stationnaires autorisées par des surfaces fermées sont analysées. Ces structures définiront les caractéristiques des fractions qui prédisent la théorie dans un espace-temps normal de quatre dimensions.

4.- Hépatphère

Dans toutes les topologies qui peuvent être obtenus, les mathématiciens ont choisi une topologie spéciale pour ses caractéristiques: Hépatphère (équivalent en sept dimensions de la sphère). Ce modèle décrit toutes les structures allant du plus petit atome à la plus grande galaxie.

Si cette sphère à sept dimensions se déforme, la dissimulation des symétries et la rupture brutale peuvent apparaître. Pour ces raisons, ce modèle a été considéré comme optimal.

Serait-il possible de sonder et de détecter physiquement cette sphère ? Selon des calculs récents, la longueur de la circonférence de cette hépatopathe est comprise entre 10 et 32 cm. Cette dimension est située à côté de la plus petite distance avec le sens physique utilisé en physique, la distance de Planck.

La différence du principe d'incertitude de Heisenberg pour sonder l'hépatphère de Kaluza/ /Klein serait 1019 fois plus grande que la masse du proton. A ce niveau énergétique, nous pouvons voir une structure spatiale temporaire en onze dimensions. Mais pour y parvenir, nous aurions besoin d'un accélérateur de fractions aussi grand que la Voie lactée d'Ortz.

Cependant, dans les recherches menées ces dernières années, d'importants problèmes ont surgi, qui souvent ne sont pas conciliateurs avec le monde à quatre dimensions que nous connaissons et étudions. Un de ces problèmes est: Sur tous les mondes à onze dimensions analysées, l'existence de neutrinos dextrogyrus et de neutrinos lévitique est prédite. Cela ne correspond pas à l'expérience que nous avons. Dans notre monde, tous les neutrinos sont légères.

Une petite particule en forme de cordon ou de corde a une seule dimension. Dans la théorie des cordes, les cordes sont extrêmement petites et se déplacent dans un espace et un temps similaire de 10 dimensions. Les propriétés de la théorie des supercordes pour les pages de l'univers sont actuellement étudiées et sont étroitement liées à certains problèmes majeurs de mathématiques contemporaines.

Il y a un autre problème. Les dimensions enroulées sur les mondes de Kaluza/Klein donnent une grande courbure à d'autres dimensions spatio-temporelles. Cela crée une grande contradiction avec les observations astronomiques actuelles, car selon ces dernières la courbure moyenne de l'univers est pratiquement nulle.

5.- Perspectives actuelles

Les problèmes mentionnés et les infinis de la gravitation quantique ont été présents ces dernières années. Actuellement (selon les progrès réalisés au cours de 1985) on parle d'un univers de dix dimensions entre scientifiques et la soi-disant théorie des Supercordes (1) pour expliquer cet univers a généré de grandes attentes.

À ce stade, nous nous rappellerons que le développement des théories gaudí non abéliennes utilisées a pris une dizaine d'années à se développer. C'est pourquoi, pour renforcer les relations entre la supergravité et les théories de Kaluza/Klein, il est possible qu'elles passent plusieurs années. En attendant, il faudra développer des travaux théoriques et mathématiques spéciaux qui impliquent ces théories.

Le binôme Mathématique/Physique est de plus en plus important. La découverte mathématique qui a conduit la théorie physique de la supergravité était le nombre le plus anticommutant. Les mathématiques qui ont besoin de la théorie physique de la gravitation quantique sont encore à créer.

OBSERVATIONS

    Dans cette nouvelle théorie, les fractions de base (quantos) sont remplacées par des cordes en vibration. Chaque vibration correspond à une fraction. Dans cette superthéorie se combinent la théorie des cordes et la supersymétrie.
Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila