Theories of Kaluza and Klein: an eleven dimensional world

Two of the four basic forces we have to define matter have joined experimentally (electromagnetic and weak). To unify violent force, the Theories of the Greater Union (even without experimentally demonstrating) have been created. But theoretical physicists seek a superbroad theory to unite the four forces in a theoretical framework. For this purpose, the so-called models of Supersymmetry have been created, adapting the general theories of Supergravitation. However, supergravity theory N=8 is the most appropriate to physical reality. According to this theory, space and time must be quantified and variable at supershort distances.

1.- Kaluza model and gravitation

At a distance, the cable looks like a curved line. Closer, however, we see that the point P is a circle. It is possible that in the space of the tridimensional what we normally consider as a point is a small circle around another spatial dimension. This is the basic idea of Kaluza and Klein in the unifying theory of electromagnetic and gravitational forces.

Einstein's ancient dream (to unite the gravitational and electromagnetic field with the geometric description) was reinvented by the Polish physicist Theordor Kaluza and around 1921 he tried to express by geometry Maxwell's electromagnetic theory. But to carry out this project it was necessary to remodel own geometry so that the Electromagnetic would be molded within that geometry.

To achieve this, Kaluza postulated an additional spatial dimension, so the geometry that depends on nature would have four spatial dimensions and a time. Gravitation in this five-dimensional world would be the result of the sum of normal gravity and Maxwell's electromagnetic field. If we were able to expand our perception in five dimensions, we would encounter a single force field: the gravitational one. According to this theory, the electromagnetic wave would be the undulation of the fifth dimension.

Kaluza's theory obtained a great mathematical success. But he also had an unbeatable tail. That is, if the space universe is four dimensions, why can't the fourth dimension be physically grasped? Will that fourth dimension be just a mathematical nail?

2.- Pentadimensional structure of Klein

In 1926 the Swedish physicist Oscar Klein tried to demonstrate the compatibility of the pentadimensional structure and quantum mechanics of Kaluza. For this purpose, it provided a new version of the Schrödinger equation adapted to the five dimensions. For Klein, the fourth spatial dimension has a real existence.

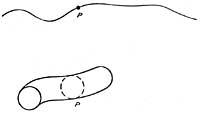
To better understand this, let's assume a line and a circle associated with each point of that line. The union of the line of a dimension with the circle of a dimension creates a two-dimensional cylinder. Suppose also a plane in which all points of that plane are adapted to a circle, then the union between the two-dimensional plane and the circle of a dimension will create one in three continuous dimensions.

With the same reasoning we can guess that at each point we add a three-dimensional continuum and a circle, which are curled in the fourth dimension. These loops would not be curled in space, because they are not within space. What these spirals do is expand space.

Klein began calculating the circles of these circles that create a five-dimensional universe. For this purpose, it took into account the charges of electrons and other particles, such as the gravitational forces between them. In case of calculations, he indicated that the length of these circles would be between 10 and 30 cm.

Its small number indicates why the fifth dimension cannot be correctly perceived. This figure is so small that, in addition to a living being, no atom could move through these dimensions.

This dimension is situated within the atom. To detect such a subtle structure, we should have an accelerator of fractions of several years of light.

3.- Generalization of Kaluza-Klein models: a world of eleven dimensions

The Kaluza/Klein model was forgotten for several years. However, in recent years the passion of this model has emerged among scientists, but now in a different context: That is, in the context of the Theories of Greater Union and Supergravitational Theories.

With the aim of uniting the forces of nature, seven unknown dimensions of the Universe have been proposed in a theory. It can be expressed as a small compact structure, as if each point of the sphere had at every moment an attached sphere. The spheres located in the intersections of the coordinates lines are additional dimensions grouped postulated in the new theory. The spheres are tangent in each point with respect to the plane. In addition, the sphere and the plane generate only four dimensions and not 11 of the theory. The four dimensions are the four coordinates that define a point.

The theory of Kaluza/Klein has been reintegrated into the field of Physics, assuming that the symmetry of the fields of force is the result of an internal geometric structure in Nature. Furthermore, gauge symmetries are forms of geometry added to the new spatial dimensions.

The problems that the generalized theory of Kaluza/Klein should cover are the following three. First you will have to fill a fermonic field to indicate the fermions in our universe. It should also indicate at least one bosomic field and, of course, the gravitational field (origin of the hidden spiral dimensions). The model that meets all these requirements is a version of supergravity 11. Thus, the modern theory of Kaluza/Klein postulates an 11-dimensional universe. Seven of these eleven dimensions would be rolled up to a level in which they would be hidden for direct observation.

To the dimensions in which they appear rolled correspond a large number of types of topologies, so you have to carry out a concrete process to choose the most appropriate:

    Solve equations of supergravity. Some of these measures could correspond to four space-time dimensions and a closed topological form of seven dimensions. Then, we would study the set of symmetries of each surface corresponding to the resolution of equations. The set of symmetries defines us the non-abelina gauge theory which must join to gravity. The different closed surfaces present different types of symmetries, and each of them defines a different theory of the Great Unions.
  1. Finally, the stationary wave structures allowed by closed surfaces are analyzed. These structures will define the characteristics of the fractions predicted by the theory in a normal four-dimensional space-time.

4.- Heptasphere

In all the topologies that can be achieved, mathematicians have chosen a special topology for their characteristics: Heptasphere (equivalent in seven dimensions of the sphere). Through this model, all structures ranging from the smallest atom to the largest galaxy are described.

If this seven-dimensional sphere is deformed, the concealment of symmetries and sudden rupture may appear. For these reasons this model has been considered optimal.

Would it be possible to physically probe and detect this sphere?. According to recent calculations, the length of the circumference of this heptasphere is between 10 and 32 cm. This dimension is situated next to the smallest distance with physical sense used in Physics, the distance of Planck.

The difference in Heisenberg's uncertainty principle to probe the heptasphere of Kaluza/Klein would be 1019 times greater than the mass of the proton. In this energy level we can see a temporary spatial structure of eleven dimensions. But to achieve this we would need an accelerator of fractions as large as the Milky Way of Ortz.

However, in the research carried out in recent years, important problems have arisen which, on many occasions, are not conciliatory with the four-dimensional world that we know and study. One of these problems is: In all the worlds of eleven dimensions analyzed, the existence of dextrógiro and levógiro neutrinos is predicted. This does not correspond to the experience we have. In our world all neutrinos are levógiros.

A small particle in the shape of a cord or cord has a single dimension. In the theory of superstrings, the strings are extremely small and move in a similar space and time of 10 dimensions. The properties of superstring theory for the pages of the universe are currently being investigated and are closely related to some important problems of contemporary mathematics.

There is another problem. The dimensions wound on the worlds of Kaluza/Klein give a great curvature to other space-time dimensions. This creates a great contradiction with the current astronomical observations, since according to the latter the average curvature of the universe is practically null.

5.- Current perspectives

The above-mentioned problems and infinite quantum gravitation have been present in recent years. Today (according to the advances made throughout 1985) there is talk of a universe of ten dimensions between scientists and the so-called Superstring theory (1) to explain this universe has generated great expectations.

At this point, we will remember that the development of non-Abelian gaudi theories used took about ten years to develop. For this reason, to reinforce the relations between supergravity and the theories of Kaluza/Klein, it is possible that several years will pass. In the meantime, we will have to develop special theoretical and mathematical works involving these theories.

The Mathematical/Physics binomial has more and more importance. The mathematical discovery that prompted the physical theory of supergravity was the most anticommuting number. The mathematics which needs the physical theory of quantum gravitation is yet to be created.

OBSERVATIONS

    In this new theory, basic fractions (quantos) are replaced by strings in vibration. A fraction corresponds to each vibration. In this supertheory combine the theory of strings and supersymmetry.
Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila