Corpos platónicos
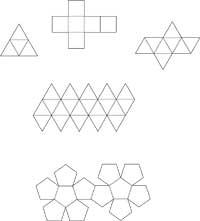
Non, eses corpos fortes, esveltos e morenos que vemos ao sol ou á sombra durante as vacacións de verán. Non, tampouco son os que fan culturismo. Tamén está equivocado o que pensou nos cordeiros asados que se serven en “Estudios”. Os corpos platónicos son só poliedros regulares. Aos poliedros regulares chamóuselles tamén corpo cósmico ou corpo platónico polas formas que Platón aplica na súa obra Timeo paira explicar cientificamente os fenómenos. En total son cinco: tetraedro, hexaedro (cubo), octaedro, dodecaedro e ikosaedro (figura 1). O cinco caracterízanse por estar formadas por polígonos regulares do mesmo tipo e convexos; o tetraedro, octaedro e icosaedro están formados por triángulos equiláteros, o hexaedro cadrado e o dodecaedro en pentágono.
Nombredelescanterpinactetraedro4 triángulo64Hexaedroa6 cuadratu128Octaedro8 triangulo126 Dodecaedroa12 pentagono3020Ikosaedroaedro20 triangulo 3012Fórmula de Euler |
Lados + Vértices = Arestas + 2 |

Platón (a.C.) 427-347) non supuxo en si mesmos resultados técnicos paira as matemáticas. Con todo, foi o verdadeiro centro da actividade matemática da época e ademais de influír persoalmente no seu desenvolvemento, tamén a dirixiu. Nas portas de acceso ao colexio de Atenas dicíase: “Que non entre ninguén que non saiba xeometría”. A súa responsabilidade matemática, máis que como matemática, deuna a coñecer como matemática. Parece que o recoñecemento de Platón das matemáticas non proviña do seu mestre Sócrates. Arquitecto, o seu amigo, foi o que se achegou ás matemáticas Platón. No ano 300 visitoulle en Sicilia. Quizá alí coñeceu por primeira vez os cinco corpos regulares citados.
O tetraedro, o hexaedro, o octaedro e o ikosaedro relacionábanse cos catro elementos de Enpedokles nun esquema cósmico que fascinou ao home durante séculos (Figura 2). Doutra banda, os Pitágoros admiraban ao dodecaedro. Platón recoñeceu o dodecaedro, quinto e último corpo regular, como símbolo do universo.
O lume, o aire, a auga e o chan únense co tetraedro, o octaedro, o ikosaedro e o hexaedro respectivamente. Fóra dos do hexaedro, dado que os lados dos outros poliedros son triángulos equiláteros e, por tanto, similares, os elementos correspondentes, lume, aire e auga, poderían volverse mutuos, pero non terras, xa que as caras do hexaedro son cadradas. Os cadrados non se poden descompor en triángulos equiláteros, só se poden descompor en triángulos rectilíneos isósceles. Por outra banda, o poliedro de menor volume respecto da súa superficie é o tetraedro, de onde parece desprenderse a unión ao lume. O máis voluminoso en superficie é o ikosaedro, polo que se uniu á auga. O hexaedro, pola súa banda, é estable respecto da súa base, polo que se uniu ao terreo. Ao virar o octaedro agarrado por dous vértices opostos, adecuouse ao aire que se move. O poliedro regular quinto, dodecaedro, está formado por pentágonos e os pentágonos tampouco poden descomporse en triángulos equiláteros, e o dodecaedro ten 12 lados, reflexo dos 12 signos do zodiaco, de aí a súa relación co universo.
En Timeo, onde leva o nome do seu interlocutor principal, expuxo as súas ideas sobre os corpos regulares platónicos. Non sabemos si o de Timeo Lokia existiu realmente ou o inventou Platón coa escusa de explicar as súas ideas pitagóricas.
Platón escribiu este coloquio aos 70 anos, no que nos dá a primeira pegada exacta da relación entre os catro elementos e os corpos regulares, pero moitos dos episodios desta fantasía débense aos pitagóricos. Segundo Proklo, Pitágoras construíu a imaxe cósmica, pero o escolástico Suidas dicía que Teeteto (amigo de Platón, a. C.). Nacido no ano 414, foi o primeiro que escribiu respecto diso.
Euklides dedicou o último libro de “Elementos”, o xiii, aos poliedros regulares. Nel deunos relacións entre os bordos dos poliedros e os radios das esferas inscritas e circunscritas. Finalmente, como lema aparecía o teorema que se engadiu máis tarde: ademais do cinco poliedros regulares coñecidos, non hai outro poliedro regular.

XIII Elementos de Euklides. segundo un colexio de data descoñecida do libro, os pitagóricos só coñecían tres corpos regulares e o octaedro e o icosaedro foron coñecidos por Teeteto. Con todo, parece que Teeteto realizou un das análises sistemáticas entón dos poliedros regulares e el mesmo escribiu o teorema de que hai cinco e só cinco poliedros regulares. Apika, no último libro de “Elementos”, tamén son seus os cálculos das causas entre os bordos dos corpos regulares e o radio da esfera circunscrita.
Tanto en aritmética como en xeometría, Platón situouse a favor da matemática pura, fronte ás concepcións materialistas do artesán e técnico. Plutarko recolleu na súa obra “A vida de Marcelo” o enfado de Platón ante o uso de artificios mecánicos na xeometría; Platón consideraba este uso como a corrupción e a simple cancelación do ben existente na xeometría, dando as súas costas descaradamente a obxectos sen corpo de pura intelixencia. En consecuencia, Platón puido ser, en gran medida, responsable da principal restrición ás construcións de xeometría que só se poden realizar mediante compás e regra. A razón desta redución non foi probablemente a simplicidad dos instrumentos utilizados, senón a simetría dos construídos: calquera diámetro do círculo é o eixo de simetría; calquera punto da recta é o centro de simetría; calquera unión cunha recta é o seu eixo de simetría.
A filosofía platónica, divinizando as ideas, debía pór en primeiro lugar a recta e a circunferencia entre todas as figuras xeométricas. De forma similar, Platón enxalzou o triángulo. Paira Platón, as diferenzas do cinco poliedros regulares non eran meros triángulos, cadrados e pentágonos. Por exemplo, cada lado do tetraedro estaba formado por seis triángulos rectilíneos menores (obtidos por alturas), descompóndose o tetraedro en 24 triángulos rectos escalenos. Así mesmo, octaedro e icosaedro en 48 e 120 triángulos rectilíneos escalenos, respectivamente, e hexaedro en 24 triángulos rectos isósceles.
Platón deu un papel especial ao dodecaedro, como representante do universo, dicindo que Deus o utilizou na súa totalidade” (Timeo, 55). Platón consideraba o dodecaedro como un conxunto de 360 triángulos rectilíneos escalenos, xa que debuxando nos pentágonos as cinco diagonais e as intermedias quedan 30 triángulos.
Ao unir o catro primeiros poliedros regulares cos catro elementos do universo, Timeon deu una bonita teoría unificada da materia, segundo a cal todo está formado por triángulos rectilíneos ideais e a fisiología, no seu conxunto, do mesmo xeito que a ciencia da materia inerte, está baseada no funcionamento de devanditos triángulos. O crecemento do corpo dun animal, por exemplo, explicouno:
“A Constitución da Criatura, na súa totalidade, cando aínda é nova e os seus compoñentes son de recente construción, as súas puntas están fortemente interrelacionadas… Calquera dos triángulos que compoñen os alimentos e bebidas…, máis antigo e máis débil que os seus, córtano os seus triángulos recentemente feitas e por iso saca o mellor proveito e iso é o que fai crecer ao animal.Na
vellez, pola contra, os triángulos que forman o corpo están tranquilos polo seu uso e non poden cortar os triángulos do alimento que inxeren, mentres que as sarquinas que veñen do exterior parten con facilidade as súas e a criatura esgótase e cae.”





