Cuerpos platónicos
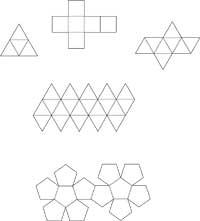
No, esos cuerpos fuertes, esbeltos y morenos que vemos al sol o a la sombra durante las vacaciones de verano. No, tampoco son los que hacen culturismo. También está equivocado lo que ha pensado en los corderos asados que se sirven en “Platós”. Los cuerpos platónicos son sólo poliedros regulares. A los poliedros regulares se les ha llamado también cuerpo cósmico o cuerpo platónico por las formas que Platón aplica en su obra Timeo para explicar científicamente los fenómenos. En total son cinco: tetraedro, hexaedro (cubo), octaedro, dodecaedro e ikosaedro (figura 1). Las cinco se caracterizan por estar formadas por polígonos regulares del mismo tipo y convexos; el tetraedro, octaedro e icosaedro están formados por triángulos equiláteros, el hexaedro cuadrado y el dodecaedro en pentágono.
Nombredelescanterpinactetraedro4 triángulo64Hexaedroa6 cuadratu128Octaedro8 triangulo126 Dodecaedroa12 pentagono3020Ikosaedroaedro20 triangulo 3012Fórmula de Euler |
Lados + Vértices = Aristas + 2 |

Platón (a.C.) 427-347) no supuso en sí mismo resultados técnicos para las matemáticas. Sin embargo, fue el verdadero centro de la actividad matemática de la época y además de influir personalmente en su desarrollo, también la dirigió. En las puertas de acceso al colegio de Atenas se decía: “Que no entre nadie que no sepa geometría”. Su responsabilidad matemática, más que como matemática, la dio a conocer como matemática. Parece que el reconocimiento de Platón de las matemáticas no provenía de su maestro Sócrates. Arquitecto, su amigo, fue el que se acercó a las matemáticas Platón. En el año 300 le visitó en Sicilia. Quizá allí conoció por primera vez los cinco cuerpos regulares citados.
El tetraedro, el hexaedro, el octaedro y el ikosaedro se relacionaban con los cuatro elementos de Enpedokles en un esquema cósmico que ha fascinado al hombre durante siglos (Figura 2). Por otro lado, los Pitágoros admiraban al dodecaedro. Platón reconoció el dodecaedro, quinto y último cuerpo regular, como símbolo del universo.
El fuego, el aire, el agua y el suelo se unen con el tetraedro, el octaedro, el ikosaedro y el hexaedro respectivamente. A excepción de los del hexaedro, dado que los lados de los otros poliedros son triángulos equiláteros y, por tanto, similares, los elementos correspondientes, fuego, aire y agua, podrían volverse mutuos, pero no tierras, ya que las caras del hexaedro son cuadradas. Los cuadrados no se pueden descomponer en triángulos equiláteros, sólo se pueden descomponer en triángulos rectilíneos isósceles. Por otra parte, el poliedro de menor volumen respecto a su superficie es el tetraedro, de donde parece desprenderse la unión al fuego. El más voluminoso en superficie es el ikosaedro, por lo que se ha unido al agua. El hexaedro, por su parte, es estable respecto a su base, por lo que se ha unido al terreno. Al girar el octaedro agarrado por dos vértices opuestos, se ha adecuado al aire que se mueve. El poliedro regular quinto, dodecaedro, está formado por pentágonos y los pentágonos tampoco pueden descomponerse en triángulos equiláteros, y el dodecaedro tiene 12 lados, reflejo de los 12 signos del zodiaco, de ahí su relación con el universo.
En Timeo, donde lleva el nombre de su interlocutor principal, expuso sus ideas sobre los cuerpos regulares platónicos. No sabemos si el de Timeo Lokia existió realmente o lo inventó Platón con la excusa de explicar sus ideas pitagóricas.
Platón escribió este coloquio a los 70 años, en el que nos da la primera huella exacta de la relación entre los cuatro elementos y los cuerpos regulares, pero muchos de los episodios de esta fantasía se deben a los pitagóricos. Según Proklo, Pitágoras construyó la imagen cósmica, pero el escolástico Suidas decía que Teeteto (amigo de Platón, a. C.). Nacido en el año 414, fue el primero que escribió al respecto.
Euklides dedicó el último libro de “Elementos”, el xiii, a los poliedros regulares. En él nos dio relaciones entre los bordes de los poliedros y los radios de las esferas inscritas y circunscritas. Finalmente, como lema aparecía el teorema que se añadió más tarde: además de los cinco poliedros regulares conocidos, no hay otro poliedro regular.

XIII Elementos de Euklides. según un colegio de fecha desconocida del libro, los pitagóricos sólo conocían tres cuerpos regulares y el octaedro y el icosaedro fueron conocidos por Teeteto. Sin embargo, parece que Teeteto realizó uno de los análisis sistemáticos entonces de los poliedros regulares y él mismo escribió el teorema de que hay cinco y sólo cinco poliedros regulares. Apika, en el último libro de “Elementos”, también son suyos los cálculos de las causas entre los bordes de los cuerpos regulares y el radio de la esfera circunscrita.
Tanto en aritmética como en geometría, Platón se posicionó a favor de la matemática pura, frente a las concepciones materialistas del artesano y técnico. Plutarko recogió en su obra “La vida de Marcelo” el enfado de Platón ante el uso de artificios mecánicos en la geometría; Platón consideraba este uso como la corrupción y la simple cancelación del bien existente en la geometría, dando su espalda descaradamente a objetos sin cuerpo de pura inteligencia. En consecuencia, Platón pudo ser, en gran medida, responsable de la principal restricción a las construcciones de geometría que sólo se pueden realizar mediante compás y regla. La razón de esta reducción no fue probablemente la simplicidad de los instrumentos utilizados, sino la simetría de los construidos: cualquier diámetro del círculo es el eje de simetría; cualquier punto de la recta es el centro de simetría; cualquier unión con una recta es su eje de simetría.
La filosofía platónica, divinizando las ideas, debía poner en primer lugar la recta y la circunferencia entre todas las figuras geométricas. De forma similar, Platón ensalzó el triángulo. Para Platón, las diferencias de los cinco poliedros regulares no eran meros triángulos, cuadrados y pentágonos. Por ejemplo, cada lado del tetraedro estaba formado por seis triángulos rectilíneos menores (obtenidos por alturas), descomponiéndose el tetraedro en 24 triángulos rectos escalenos. Asimismo, octaedro e icosaedro en 48 y 120 triángulos rectilíneos escalenos, respectivamente, y hexaedro en 24 triángulos rectos isósceles.
Platón dio un papel especial al dodecaedro, como representante del universo, diciendo que “Dios lo utilizó en su totalidad” (Timeo, 55). Platón consideraba el dodecaedro como un conjunto de 360 triángulos rectilíneos escalenos, ya que dibujando en los pentágonos las cinco diagonales y las intermedias quedan 30 triángulos.
Al unir los cuatro primeros poliedros regulares con los cuatro elementos del universo, Timeon dio una bonita teoría unificada de la materia, según la cual todo está formado por triángulos rectilíneos ideales y la fisiología, en su conjunto, al igual que la ciencia de la materia inerte, está basada en el funcionamiento de dichos triángulos. El crecimiento del cuerpo de un animal, por ejemplo, lo explicó:
“La Constitución de la Criatura, en su totalidad, cuando todavía es joven y sus componentes son de reciente construcción, sus puntas están fuertemente interrelacionadas… Cualquiera de los triángulos que componen los alimentos y bebidas…, más antiguo y más débil que los suyos, lo cortan sus triángulos recién hechas y por eso saca el mejor provecho y eso es lo que hace crecer al animal.En la vejez, por el contrario, los triángulos que forman el cuerpo están tranquilos por su uso y no pueden cortar los triángulos del alimento que ingieren, mientras que las sarquinas que vienen del exterior parten con facilidad las suyas y la criatura se agota y cae.”





