Corps platoniques
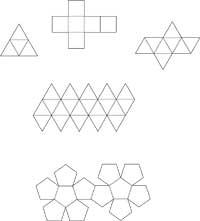
Non, ces corps forts, élancés et bruns que nous voyons au soleil ou à l'ombre pendant les vacances d'été. Non, ce ne sont pas non plus ceux qui font du culturisme. Vous avez également tort ce que vous avez pensé aux agneaux rôtis qui sont servis dans “Platós”. Les corps platoniques ne sont que des polyèdres réguliers. Les polyèdres réguliers sont aussi appelés corps cosmique ou corps platonique par les formes que Platon applique dans son œuvre Timée pour expliquer scientifiquement les phénomènes. Au total, il y en a cinq : tétraèdre, hexaèdre (cube), octaèdre, dodécaèdre et ikosaèdre (figure 1). Les cinq sont composées de polygones réguliers du même type et de convexes ; le tétraèdre, l'octaèdre et l'icosaèdre sont constitués de triangles équilatéraux, l'hexaèdre carré et le dodécaèdre en pentagone.
Nomdusscanterpinactetraedro4 triangle64Hexaedroa6 carratu128Octaedro8 triangule126 Dodecaedroa12 pentagono3020Ikosaedroaedro20 triangle 3012Formule d'Euler |
Côtés + Sommets = Arêtes + 2 |

Platon (a.C.) 427-347) n'a pas supposé lui-même des résultats techniques pour les mathématiques. Cependant, il a été le véritable centre de l'activité mathématique de l'époque et en plus d'influencer personnellement son développement, il a également dirigé. Aux portes d’accès au collège d’Athènes, on disait: “Que personne ne connaisse la géométrie”. Sa responsabilité mathématique, plutôt que comme mathématique, l'a fait connaître comme mathématique. Il semble que la reconnaissance de Platon des mathématiques ne provenait pas de son maître Socrate. Architecte, son ami, est celui qui a approché les mathématiques Platon. En l'an 300, il lui visita en Sicile. Il y a peut-être rencontré pour la première fois les cinq corps réguliers cités.
Le tétraèdre, l'hexaèdre, l'octaèdre et l'ikosaèdre étaient liés aux quatre éléments d'Enpedokles dans un schéma cosmique qui a fasciné l'homme pendant des siècles (figure 2). D'autre part, les Pythagores admiraient le dodécaèdre. Platon a reconnu le dodécaèdre, cinquième et dernier corps régulier, comme symbole de l'univers.
Le feu, l'air, l'eau et le sol se lient avec le tétraèdre, l'octaèdre, l'ikosaèdre et l'hexaèdre respectivement. A l'exception de ceux de l'hexaèdre, puisque les côtés des autres polyèdres sont des triangles équilatéraux et donc similaires, les éléments correspondants, le feu, l'air et l'eau, pourraient devenir mutuels, mais pas des terres, puisque les faces de l'hexaèdre sont carrées. Les carrés ne peuvent pas être décomposés en triangles équilatéraux, ils peuvent seulement être décomposés en triangles droits isocèle. D'autre part, le polyèdre de moindre volume par rapport à sa surface est le tétraèdre, d'où l'union au feu semble se détacher. Le plus volumineux en surface est l'ikosaèdre, de sorte qu'il a rejoint l'eau. L'hexaèdre, quant à lui, est stable par rapport à sa base, de sorte qu'il a rejoint le terrain. En tournant l'octaèdre saisi par deux sommets opposés, il a été adapté à l'air qui se déplace. Le polyèdre régulier cinquième, dodécaèdre, est composé de pentagones et les pentagones ne peuvent pas non plus se décomposer en triangles équilatéraux, et le dodécaèdre a 12 côtés, reflet des 12 signes du zodiaque, d'où sa relation avec l'univers.
À Timée, où il porte le nom de son principal interlocuteur, il a exposé ses idées sur les corps réguliers platoniciens. Nous ne savons pas si le de Timeo Lokia a réellement existé ou inventé Platon sous prétexte d'expliquer ses idées pythagoriques.
Platon a écrit ce colloque à 70 ans, dans lequel il nous donne la première empreinte exacte de la relation entre les quatre éléments et les corps réguliers, mais beaucoup d'épisodes de ce fantasme sont dus à des pythagoriciens. Selon Proklo, Pythagore construit l'image cosmique, mais le scolastique Suidas dit que Teeteto (ami de Platon, a. C.). Né en 414, il fut le premier à écrire à ce sujet.
Euklides a consacré le dernier livre de “Eléments”, le xiii, aux polyèdres réguliers. Il nous a donné des relations entre les bords des polyèdres et les rayons des sphères inscrites et circonscrites. Enfin, comme devise apparaissait le théorème qui a été ajouté plus tard: en plus des cinq polyèdres réguliers connus, il n'y a pas d'autre polyèdre régulier.

XIII Éléments d'Euklides. Selon un collège de date inconnue du livre, les pythagoriciens ne connaissaient que trois corps réguliers et l'octaèdre et l'icosaèdre ont été connus par Teeteto. Cependant, il semble que Teeteto a effectué une des analyses systématiques puis des polyèdres réguliers et lui-même a écrit le théorème qu'il ya cinq et seulement cinq polyèdres réguliers. Apika, dans le dernier livre de «Eléments», sont aussi les calculs des causes entre les bords des corps réguliers et le rayon de la sphère circonscrite.
En arithmétique et en géométrie, Platon se positionna en faveur de la pure mathématique, face aux conceptions matérialistes de l'artisan et technique. Plutarko ramassé dans son travail “La vie de Marcel” la colère de Platon face à l'utilisation d'artifices mécaniques dans la géométrie; Platon considérait cet usage comme la corruption et la simple annulation du bien existant dans la géométrie, donnant son dos sans vergogne à des objets sans corps de pure intelligence. En conséquence, Platon pourrait être, dans une large mesure, responsable de la principale restriction aux constructions de géométrie qui ne peuvent être effectuées que par mesure et règle. La raison de cette réduction n'était probablement pas la simplicité des instruments utilisés, mais la symétrie des instruments construits: tout diamètre du cercle est l'axe de symétrie; tout point de la droite est le centre de symétrie; toute union avec une droite est son axe de symétrie.
La philosophie platonicienne, divinisant les idées, devait mettre en premier lieu la droite et la circonférence entre toutes les figures géométriques. De même, Platon a élevé le triangle. Pour Platon, les différences des cinq polyèdres réguliers n'étaient pas de simples triangles, carrés et pentagones. Par exemple, chaque côté du tétraèdre était composé de six petits triangles rectilignes (obtenus par des hauteurs), décomposant le tétraèdre en 24 triangles droits échelons. En outre, l'octaèdre et l'icosaèdre dans 48 et 120 triangles rectilignes scalaires, respectivement, et l'hexaèdre dans 24 triangles droits isocèle.
Platon a donné un rôle particulier au dodécaèdre, en tant que représentant de l'univers, en disant que «Dieu l'a utilisé dans son intégralité» (Timée, 55). Platon considérait le dodécaèdre comme un ensemble de 360 triangles rectilignes échelons, car en dessinant sur les pentagones les cinq diagonales et les intermédiaires restent 30 triangles.
En joignant les quatre premiers polyèdres réguliers aux quatre éléments de l'univers, Timeon donna une belle théorie unifiée de la matière, selon laquelle tout est formé par des triangles linéaires idéaux et la physiologie, dans son ensemble, comme la science de la matière inerte, est basée sur le fonctionnement de ces triangles. La croissance du corps d'un animal, par exemple, l'a expliqué:
« La Constitution de la Créature, dans sa totalité, quand elle est encore jeune et ses composants sont de construction récente, ses pointes sont fortement liées… N'importe lequel des triangles qui
composent les aliments et les boissons…, plus ancien et plus faible que les siens, le coupent ses triangles nouvellement faits et c'est pourquoi il tire le meilleur profit et c'est ce qui fait croître l'animal.Dans la vieillesse, au contraire, les triangles qui forment la créature dehors





