Essais géométriques
Le théorème de Pythagore n'est pas le seul qui peut être démontré par la géométrie. Beaucoup de similitudes et de différences mathématiques peuvent être contrastées en utilisant des figures géométriques. Dans cet article, nous vous en présentons quelques-unes.
La première figure montre la vérification géométrique simple d'une des formules de base:
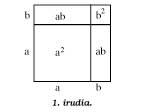
(a + b)2 = a2 + 2ab + b2
Dans la deuxième figure si elle est similaire à la formule ci-dessus
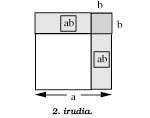
(a - b)2 = a2 - 2ab + b2
Il s'agit de l'expression géométrique correspondant à la formule. Notez que le carré correspondant à l'addition b2 se trouve dans le rectangle correspondant à l'addition ab et que le carré a2 est enlevé deux fois ( -2ab).
Si dans la figure 2 nous extrayons le carré b2 par le carré a2 (figure 3), la surface tracée, 2ab, ne change pas. On observe maintenant la différenciation suivante:
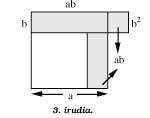
2ab a2 + b2
Poursuivant les différences, la figure 4 montre la démonstration géométrique d'une autre différenciation équivalente à la précédente :
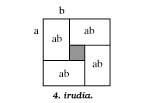
4ab (a + b) 2
Calculons maintenant la somme en additionnant infiniment (Figure 5). En ajoutant la moitié au carré du côté 1 nous obtenons 1 + 1/2 = 3/2. Additionner à cette somme le quart du carré nous avons 1 + 1/2+ + 1/4 = 3/2 + 1/4 = 7/4. Ajouter un huitième à ce dernier 1 + 1/2 + 1/4 + 1/8 = 7/4 + 1/8 = =15/8. Comme vous pouvez le voir dans la figure, cette somme est inférieure à 2. L'addition suivante 1/16 peut être insérée dans la place vide. Dans le creux restant non couvert, nous pouvons toujours inclure tous les sumands suivants. Enfin nous couvrirons le rectangle 1x2. Par conséquent,
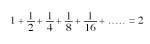
Nous obtiendrons l'égalité. Les points qui apparaissent dans cette égalité indiquent qu'il est infini additionnant.
En passant à une autre formule, nous calculerons la somme des premiers nombres. Pour cela, nous allons utiliser les carrés de base. (Voir figure 6).

Si nous continuons ainsi, nous calculerons la somme des n premiers nombres (voir figure 7).
1 + 2 + 3 + ... + n = n (n + 1)/ 2.En utilisant des carrés
de base, nous pouvons essayer d'autres formules. La figure 8 nous montre que les sommes des nombres impairs sont des nombres carrés.
Qu'en est-il des nombres pairs?. Nous allons le voir.
La somme des nombres pairs ne forment pas des carrés, mais des rectangles. (Voir figure 9).
C'est l'expression géométrique d'une autre nouvelle formule.
Nous terminerons par l'explication géométrique d'une autre formule plus compliquée:
13 + 23 + 33 +... + n3 == (1 + 2 +
3 + ... + n)2
la formule.
En suivant la ligne des expressions des formules précédentes, nous obtenons les égalités suivantes:
13 = 113 +
23 = 9 = 32 = (1 + 2)213 + 23 + 33 = 36
= 62 = (1 + 2 + 3)213 + 23 + 33 + 43 = 100 = 102 = (1
+ 2 + 3 + 4)2
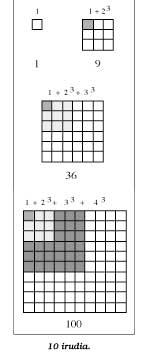
et en généralisant les résultats nous obtiendrions cette formule.





