Pruebas geométricas
El teorema de Pitágoras no es el único que puede demostrarse por geometría. Muchas de las similitudes y diferencias matemáticas se pueden contrastar utilizando figuras geométricas. En este artículo te presentamos algunas de ellas.
La primera figura muestra la verificación geométrica simple de una de las fórmulas básicas:
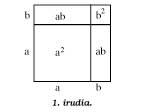
(a + b)2 = a2 + 2ab + b2
En la segunda figura si es similar a la fórmula anterior
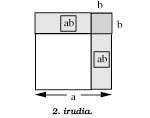
(a - b)2 = a2 - 2ab + b2
se trata de la expresión geométrica correspondiente a la fórmula. Obsérvese que el cuadrado correspondiente al sumando b2 está dentro del rectángulo correspondiente al sumando ab y que al cuadrado a2 se le quita dos veces ( -2ab).
Si en la figura 2 extraemos el cuadrado b2 por el cuadrado a2 (figura 3), la superficie trazada, 2ab, no cambia. Ahora se observa la siguiente diferenciación:
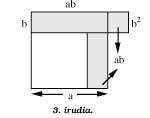
2ab a2 + b2
Continuando con las diferencias, la figura 4 muestra la demostración geométrica de otra diferenciación equivalente a la anterior:
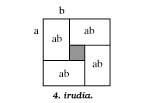
4ab (a + b) 2
Calculemos ahora la suma con infinito sumando (Figura 5). Añadiendo la mitad al cuadrado del lado 1 obtenemos 1 + 1/2 = 3/2. Sumando a esta suma la cuarta parte del cuadrado tenemos 1 + 1/2+ + 1/4 = 3/2 + 1/4 = 7/4. Añadiendo un octavo a este último 1 + 1/2 + 1/4 + 1/8 = 7/4 + 1/8 = =15/8. Como se puede apreciar en la figura, esta suma es inferior a 2. El siguiente sumando 1/16 se puede introducir en el hueco que está vacío. En el hueco que queda sin cubrir siempre podremos incluir todos los sumandos siguientes. Finalmente cubriremos el rectángulo 1x2. Por lo tanto,
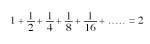
Conseguiremos la igualdad. Los puntos que aparecen en esta igualdad indican que está infinito sumando.
Pasando a otra fórmula, calcularemos la suma de los primeros números. Para ello utilizaremos los cuadrados básicos. (Ver figura 6).

Si continuamos así, calcularemos la suma de los n primeros números (ver figura 7).
1 + 2 + 3 + ... + n = n (n + 1)/ 2.Utilizando
cuadrados básicos podemos probar otras fórmulas. La figura 8 nos muestra que las sumas de los números impares son números cuadrados.
¿Qué pasa con los números pares?. Vamos a verlo.
La suma de los números pares no forman cuadrados, sino rectángulos. (Ver figura 9).
Esta es la expresión geométrica de otra nueva fórmula.
Terminaremos con la explicación geométrica de otra fórmula más complicada:
13 + 23 + 33 +... + n3 == (1 + 2 +
3 + ... + n)2
la fórmula.
Siguiendo la línea de las expresiones de las fórmulas anteriores, obtenemos las siguientes igualdad:
13 = 113 +
23 = 9 = 32 = (1 + 2)213 + 23 + 33 = 36
= 62 = (1 + 2 + 3)213 + 23 + 33 + 43 = 100 = 102 = (1
+ 2 + 3 + 4)2
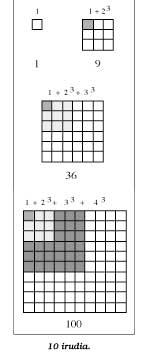
y generalizando los resultados conseguiríamos dicha fórmula.





