Baixo relatividad especial
Elhuyar. Ciencia e Técnica
En dous artigos anteriores ao , abordamos escalas de tempo e medidas mundiais comparándoas co cotián. Nesta ocasión abordaremos a Teoría da Relatividad Especial.
Aínda así, a pesar de que transcorreron 86 anos desde que se coñeceu por primeira vez esta teoría, a miúdo considéraselle algo oculto, incomprensible e sasimágico. Todos sabemos quen foi Einstein: o sabio que puxo a ciencia patas para arriba, o científico solitario e xenial que sabía moito máis que ninguén, e moitos máis tópicos. Así mitificamos Einstein, situándonos sobre un pedestal, convertémolo en inaccesible e deixamos a súa teoría paira algúns expertos. Pero podemos facer algo máis que coñecelo. En definitiva, se creemos que os habitantes do polo sur non se moven de memoria, por que non crer o que nos di a Relatividad Especial?
Nunha simple articulación non abrimos os ollos ante a nova verdade, claro, porque paira iso hai que aprender con moito esforzo, pero podemos achegarnos ás conclusións.
Por tanto, non imos mostrar ningunha demostración. Asumindo o que di a teoría e as consecuencias que dela se derivan, cambiaremos de escala para que a súa esencia inflúa na nosa vida cotiá.
Teoría da relatividad especial
A Teoría da Relatividad de Einstein consta de dous apartados: o primeiro é a Teoría da Relatividad Especial (que se representará coa abreviatura TUE), na que se analizan os obxectos de velocidade constante e o segundo, a Teoría da Relatividad Xeneral (TGV), que se tratará nun artigo posterior.
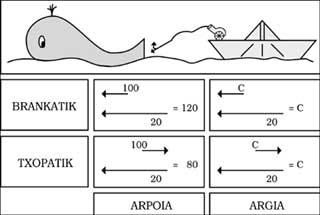
Pensemos que estamos na atalaia dun pobo da nosa costa, explorando o mar aberto, e que vemos un barco que navega a 20 km/h. Nun momento dado, o baleeiro proxecta o arpón de proa a 100 km/h. Nós, por tanto, veremos saír o arpón a 120 km/h. Pola contra, si en igualdade de condicións o arpón é lanzado desde a chopa, verémolo desde a nosa atalaia a unha velocidade de 80 km/h. Dado que os movementos do barco e arpón son de sentido contrario, as súas velocidades tenden a eliminarse entre si.
Até aquí non hai ningún obstáculo, pero agora imos pór un foco de luz no lugar do canón arpón. Como a velocidade da luz é de 300.000 km/s (indícase co símbolo c), segundo o mesmo razoamento superior, nós deberiamos ver os raios de luz desde a nosa atalaia a unha velocidade de c+ 20 e c-20. O que pasa non é iso. De feito, veremos os raios que proveñen tanto da proa como da chopa á mesma velocidade ( c). É máis, independentemente do movemento do foco de luz, a velocidade da luz manterase indefinidamente (ver figura 1).
A experiencia ensínanos este curioso comportamento que se opón á lóxica. E que a máxima velocidade posible é a da luz, é dicir, que a velocidade c non se pode superar. Por tanto, o concepto (suma ou resta de velocidades) aplicable en condicións concretas non é aplicable en condicións diferentes. Iso significa que ás veces as fórmulas (leis) aplicables non poden aplicarse noutras ocasións? Einstein respondeu que non e formulou a TUE da seguinte maneira:
- En todas as condicións son aplicables as mesmas leis.
- A velocidade da luz sempre é constante (en baleiro) e nunca se pode superar.
Paira completar o postulado anterior hai que fuxir das vellas fórmulas de sempre e utilizar as novas que inventou Lorentz (ver figura 2).
Con todo, estas novas fórmulas traen consigo una serie de consecuencias máis habituais.

Conclusións
Sen darnos conta, ao comprender e explicar o mundo que vemos, pensamos que hai velocidades infinitas. Por exemplo, vino cando sucedeu, pero paira iso a velocidade da vista debería ser infinita, ou ben tardará un tempo en percorrer o espazo desde o lugar onde ocorreu até os meus ollos. Con todo, sabemos que a velocidade máxima é c, polo que non hai velocidades infinitas. De aquí podemos sacar a primeira conclusión: hai quen opina que os sucesos que ocorren simultaneamente non son simultáneos.
Por exemplo, no centro do barco hai un pescador e como os raios que van pola proa e a chopa teñen que percorrer a mesma distancia, veraos ao mesmo tempo. Pero desde a nosa atalaia veremos que para que o raio brancótico chegue até a metade do barco ten que percorrer un camiño máis curto que o chopático (ver figura 3). Por tanto, o brancánico chega antes e non os vemos á vez!
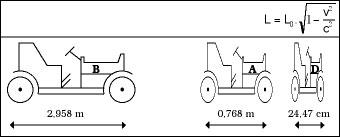
Seguindo un razoamento similar, veremos os obxectos que se moven con respecto a nós máis curtos que cando están parados, e canto maior sexa a velocidade, máis curto será o obxecto.
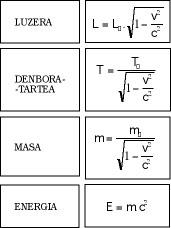
A terceira conclusión refírese ao tempo e é bastante popular. Segundo isto, nos corpos en movemento o tempo pasa máis amodo. Aínda que pareza que non hai xustificación paira iso, é una consecuencia directa das novas fórmulas. Por último, cabe mencionar que a masa en repouso dos corpos é máis lixeira que cando se moven e que a enerxía e a masa son o mesmo. O aspecto matemático de todo iso reflíctese na figura 4.
A pesar de que estas estrañas consecuencias poden ser motivadas pola teoría, alguén podía pensar que na vida cotiá nunca se viu ese efecto. A verdade é que se viron. Porque os ven todos os días... os que miran as fraccións básicas. A razón diso radica na velocidade: estes efectos só se producen cando se atopa preto da máxima velocidade en xogo (empezando polos electróns e outras fraccións), e como as velocidades que sufrimos e vemos na nosa vida están tan lonxe do máximo, non percibimos nada especial.
Non te desesperes. Para que a TUE sexa un pouco máis próxima, máis doméstica e máis comprensible, propóñovos un xogo: cambiaremos a velocidade c.
Un día en carreiras
Pensemos que a velocidade da luz é de c = 30 km/h. Con esta condición os efectos do TUE serían evidentes na nosa vida. Paira empezar, nunca poderiamos superar os 30 km/h independentemente do recurso. E que outras diferenzas observariamos entón?
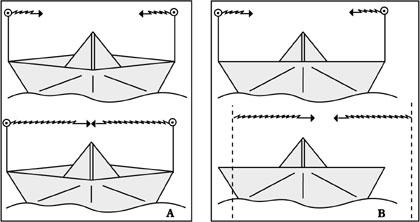
Supoñamos que é domingo e fomos a carreiras de coches. Sentámonos na bancada paira ver a carreira desde alí, pero aínda faltan uns minutos, polo que analizaremos as características de cada detalle. Vemos que a pista é una recta de 2 km de lonxitude. Así mesmo, na saída hai tres coches preparados de 3 m de lonxitude (ver figura 5). Finalmente iniciouse a carreira cos coches A e D bastante igualados (29 e 29,9 km/h respectivamente), pero o B lanzouse por avaría ou o que é imposible (5 km/h).
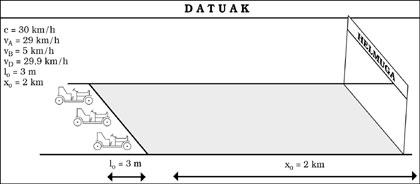
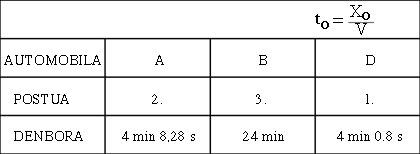
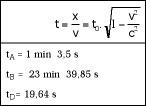
Ao pasar por diante de nós, estes coches de 3 m de lonxitude parados veremos máis curtos e, en concreto, canto máis rápido vaiamos, máis curtos parecerannos (ver figura 6). Con todo, una vez terminada a carreira, comprobamos que as tres delas teñen una lonxitude de 3 m. Mentres tanto, o gañador será D, por suposto, os tempos oficiais en meta serán os da figura 7.
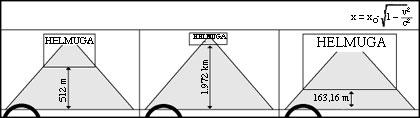
Se preguntamos aos pilotos, recibiriamos una imaxe bastante diferente. E é que aínda que o criterio do condutor B coincidise máis ou menos co noso, as opinións da e D serían diferentes. Paira A, por exemplo, a pista sería de 512 m e defendería que D tiña 163 m (ver figura 8).
O mesmo pasaría cos tempos. Creemos que mentres a distancia entre A e D é de 7,5 segundos, consideran que foi maior. E é que nós tardamos 4 minutos en ir do saída D á chegada, pero ela só tardou 19 segundos en facer o mesmo (ver figura 9). Por tanto, é máis novo que se se detivo na bancada pola velocidade. Iso é aforrar tempo!
O paradoxo dos xemelgos
Pero aquí xorde una preocupación. Canto máis lixeiro vaia o coche, máis curto vímolo e, simétricamente, os pilotos viron os obxectos da pista canto máis rápido é ir. Niso consiste precisamente a relatividad, é dicir, un pensa que o outro é máis curto, pero o outro cre que o primeiro é máis curto, e nin un nin o outro ten razón, ou ambos teñen, porque as cousas non teñen o único aspecto real, senón que dependendo do movemento do observador van adoptar distintas formas.
E agora vén a inquietude que mencionei: nós vimos aos pilotos un pouco máis novos, pero eles a nós máis antigos e non máis novos como o faría a simetría da relatividad. No caso do tempo non se cumpre a relatividad? Este nó coñécese como o paradoxo dos xemelgos. A resposta é favorable ao TUE. Vexamos por que.
Inicialmente comentouse que é aplicable naqueles casos nos que non existe aceleración TEE (velocidade constante). Se a pista está parada, podemos considerar que os coches se moven ou que os coches se moven cando están parados, e tanto un como o outro están rectos. Así que nós veremos que o tempo vai máis amodo nos coches, e os pilotos verán que o tempo vai máis amodo na pista mentres a velocidade dos automóbiles permanece constante. Aquí cúmprese a simetría da relatividad. Con todo, os automóbiles deben sufrir una aceleración no momento do seu movemento e un freado final paira deterse.
Nestes dous momentos especiais a simetría rompe e non podemos dicir que o que se move (pista ou coche) sexa o mesmo. Dado que uno deles (o coche) ten un movemento especial, o piloto sabe que non está parado. A consecuencia é que os pilotos e os de pista estean de acordo paira responder á pregunta de onde está o tempo máis lento.
Tolo no mundo
E que máis pasaría nun mundo tan baixo?
Ás 8’30 da mañá Jone e Mikel saíron de casa porque teñen un exame no Instituto de Bilbao. Ambos deixan una materia paira aprender no camiño. Jone vive en Deusto. Por tanto, saíu a pé e chegou en aproximadamente media hora, terminando a materia. Mikel, pola súa banda, ao residir en Barakaldo, colleu ás 8,30 o Tren de Alta Velocidade (29,9 km/h) e chegou ás 9, pero non tivo tempo de ler o comezo da materia, xa que apenas pasaron uns segundos na súa vida interna.
E polas mesmas razóns, os astronautas terían una vida moi dura. Supoñamos que os espazos poden circular a unha velocidade de 29,999 km/h. Neste caso, a viaxe de ida e volta á Lúa pasaría tres anos na Terra, mentres pasarían dúas semanas na vida do astronauta (incluída a estancia na superficie da Lúa). Tras quince viaxes ao longo da súa vida, o astronauta comprobaría que a súa muller e os seus fillos fosen os seus maiores.
E de todo isto, ao final que?
Devandito isto, o TUE non terá ningunha incidencia nin nos trens nin no noso modo de vida normal. Ademais, os efectos descritos non deben tomarse literalmente, senón como una aproximación. De feito, os días e os anos serían moi diferentes se houbese c = 30 km/h. O que ves non é un auténtico resumo de cousas, senón una especie de xiro e deformación. Canto maior sexa a velocidade dun obxecto, máis avermellado aparecería, etc. Pero todos estes detalles séguennos igual (os curiosos poden acudir ao cadro de Crítica da idea resumen).
A idea que temos que reter é que na natureza hai una velocidade máxima, a da luz, o que produce uns efectos estraños ou anormais cando nos achegamos a esa velocidade. E pola miña banda quixese engadir a seguinte idea: Aínda que as pegadas do TUE son incribles, son perfectamente comprensibles. O realmente sorprendente é que a teoría de Einstein só depende duns poucos científicos. Arraigamento! Non somos capaces de deseñar o motor de automóbil, pero entendemos as bases de funcionamento. Así sexa tamén co TUE!
CRÍTICA IDEA RESUMO
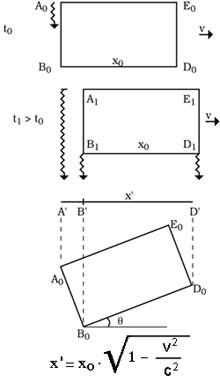
Por este motivo non podemos ver o resumo. Supoñamos un corpo A 0 B 0 D 0 E 0 que se move con velocidade v. Nós estamos aliñados coa dirección do movemento, estando a B 0 D 0 máis cerca. Como sabemos, o que sabemos nun momento determinado son os raios que chegan simultaneamente nese momento. Así, como se pode apreciar na figura, os raios que parten da 0 a B 1 e D 1 chegarán aos nosos ollos simultaneamente. O que imos ver, por tanto, tal e como explicamos no artigo, non é só un resumo B’D’, senón tamén una imaxe oculta da 0 B 0 lado A’B’. Pero esa forma de ‘A’B’D’ que vemos e o corpo co ángulo q serían iguais á imaxe virada, como se ve na imaxe. Por tanto, cando v está preto de c vemos que as cousas viran e, ao mesmo tempo, o que hai detrás das cousas é espectacular. |