Low special relativity
Elhuyar. Science and Technology
In two previous articles, we addressed time scales and global measures comparing them to everyday. On this occasion we will address the Theory of Special Relativity.
Even so, even though 86 years have passed since this theory was first known, it is often considered something hidden, incomprehensible, and sasimagical. We all know who Einstein was: the sage who turned science upside down, the lonely and brilliant scientist who knew much more than anyone, and many more topics. Thus we mystify Einstein, placing ourselves on a pedestal, making him inaccessible and leaving his theory for some experts. But we can do more than know it. In short, if we believe that the inhabitants of the south pole do not move by heart, why not believe what the Special Relativity tells us?
In a simple articulation we do not open our eyes to the new truth, of course, because for this we must learn with much effort, but we can approach the conclusions.
Therefore, we will not show any demonstration. Assuming what the theory says and the consequences that derive from it, we will change scale so that its essence influences our daily life.
Theory of Special Relativity
Einstein's Theory of Relativity consists of two sections: the first is the Theory of Special Relativity (which will be represented with the abbreviation TUE), in which the objects of constant speed are analyzed and the second, the Theory of General Relativity (TGV), which will be discussed in a later article.
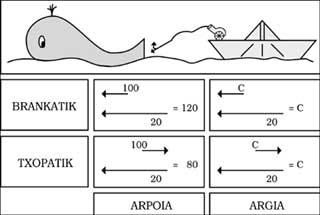
Let us think that we are at the watchtower of a village on our coast, exploring the open sea, and that we see a boat sailing at 20 km/h. At any given time, the whaler projects the bow harpoon at 100 km/h. We, therefore, will see the harpoon leave at 120 km/h. On the contrary, if on equal terms the harpoon is launched from the poplar, we will see it from our watchtower at a speed of 80 km/h. Since the movements of the boat and harpoon are of the opposite direction, their speeds tend to be eliminated from each other.
So far there is no obstacle, but now we will put a spotlight on the place of the harpoon canyon. Since the speed of light is 300,000 km/s (indicated with symbol c), according to the same superior reasoning, we should see the light rays from our watchtower at a speed of c+ 20 and c-20. What happens is not that. In fact, we will see the rays coming from both the bow and the chopa at the same speed ( c). Moreover, regardless of the movement of the light focus, the speed of light will remain indefinitely (see figure 1).
Experience teaches us this curious behavior that opposes logic. And that the maximum possible speed is that of light, that is, that the c speed cannot be overcome. Therefore, the concept (addition or subtraction of speeds) applicable under specific conditions is not applicable under different conditions. Does that mean that sometimes applicable formulas (laws) cannot be applied at other times? Einstein replied no and formulated the TEU as follows:
- The same laws apply under all conditions.
- The speed of light is always constant (empty) and can never be overcome.
To complete the above postulate, flee from the old formulas and use the new ones invented by Lorentz (see figure 2).
However, these new formulas bring with them a series of more common consequences.

Conclusions
Without realizing it, by understanding and explaining the world we see, we think there are infinite speeds. For example, I have seen it when it has happened, but for this the speed of sight should be infinite, or it will take a while to travel the space from the place where it has occurred to my eyes. However, we know that the maximum speed is c, so there are no infinite speeds. From here we can draw the first conclusion: there are those who think that the events that occur simultaneously are not simultaneous.
For example, in the center of the boat there is a fisherman and as the rays that go by the bow and the chopa have to travel the same distance, you will see them at the same time. But from our watchtower we will see that in order for the brancotic beam to reach the middle of the boat it has to travel a way shorter than the chopathic (see figure 3). Therefore, the Brancanic comes before and we do not see them at once!
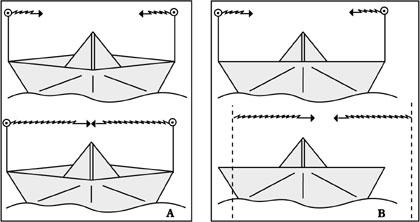
Following a similar reasoning, we will see objects moving with us shorter than when they stand, and the higher the speed, the shorter the object.
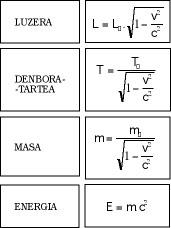
The third conclusion refers to time and is quite popular. According to this, in moving bodies time passes more slowly. Although there seems to be no justification for this, it is a direct consequence of the new formulas. Finally, it is worth mentioning that the resting mass of the bodies is lighter than when they move and that energy and mass are the same. The mathematical aspect of all this is reflected in Figure 4.
Although these strange consequences can be motivated by theory, someone might think that in everyday life that effect has never been seen. The truth is that they have been seen. Because they see them every day... those who look at the basic fractions. The reason for this lies in speed: these effects only occur when it is close to the maximum speed in play (starting with electrons and other fractions), and since the speeds we suffer and see in our life are so far from the maximum, we do not perceive anything special.
Do not despair. To make the TUE a little closer, more domestic and more understandable, I propose a game: we will change the speed c.
A day in racing
Let us think that the speed of light is c = 30 km/h. Under this condition the effects of the TEU would be evident in our lives. To begin with, we could never exceed 30 km/h regardless of the resource. And what other differences would we observe then?
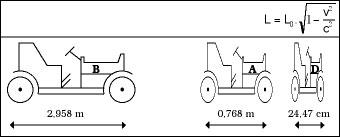
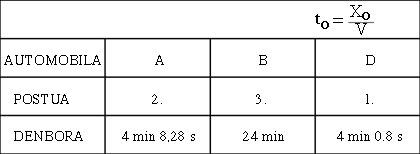
Suppose it is Sunday and we have gone to car racing. We have sat on the stand to see the race from there, but there are still a few minutes, so we will analyze the characteristics of each detail. We see that the track is a line of 2 km in length. Also, at the exit there are three cars prepared 3 m long (see figure 5). The race has finally started with the A and D cars quite matched (29 and 29.9 km/h respectively), but the B has been launched by breakdown or what is impossible (5 km/h).
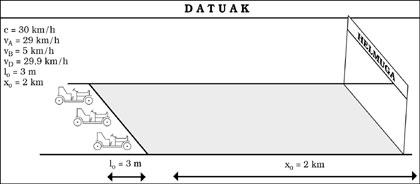
As we pass in front of us, these 3 m long cars stand we will see shorter and, in particular, the faster we go, the shorter we look (see figure 6). However, once the race is over, we check that all three of them are 3 m long. Meanwhile, the winner will be D, of course, the official times in goal will be those of figure 7.
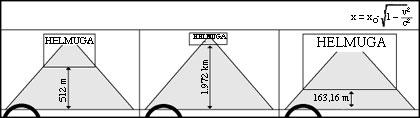
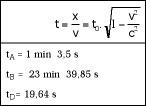
If we asked the drivers, we would receive a quite different image. Although driver B's criterion coincided more or less with ours, the opinions of A and D would be different. For A, for example, the track would be 512 m and would defend that D was 163 m (see figure 8).
The same would happen with the times. We believe that while the distance between A and D is 7.5 seconds, they consider that it has been greater. And it is that we have taken 4 minutes to go from exit D on arrival, but she has only taken 19 seconds to do the same (see figure 9). Therefore, he is younger than if he had stopped on the stand by speed. That's saving time!
The paradox of twins
But here comes a concern. The lighter the car goes, the shorter we have seen it and, symmetrically, the riders have seen the objects on the track the faster it is to go. That is precisely relativity, that is, one thinks that the other is shorter, but the other believes that the first is shorter, and neither is right, or both have, because things do not have the only real aspect, but depending on the movement of the observer they will adopt different forms.
And now comes the restlessness that I mentioned: we have seen the pilots a little younger, but they to us older and not younger as would the symmetry of relativity. In the case of time is not relativity fulfilled? This knot is known as the paradox of twins. The answer is favorable to the TEU. Let's see why.
It was initially commented that it is applicable in cases where there is no TEE acceleration (constant speed). If the track is standing, we can consider cars moving or cars moving when they are standing, and both are straight. So we'll see that time is slowing down in cars, and drivers will see that time is slowing down on the track as the speed of cars remains constant. Here the symmetry of relativity is fulfilled. However, cars must suffer an acceleration at the time of their movement and a final braking to stop.
In these two special moments the symmetry is broken and we cannot say that what moves (track or car) is the same. Since one of them (the car) has a special movement, the pilot knows he is not standing. The consequence is that drivers and runners agree to answer the question of where the slowest time is.
Crazy in the world
And what else would happen in such a low world?
At 8’30 in the morning Jone and Mikel have left home because they have an exam at the Institute of Bilbao. Both leave a subject to learn along the way. Jone lives in Deusto. Therefore, he has gone on foot and has arrived in about half an hour, having finished the subject. Mikel, for his part, when residing in Barakaldo, has taken at 8.30 the High Speed Train (29.9 km/h) and has reached 9, but has not had time to read the beginning of the course, since they have barely spent a few seconds in their internal life.
And for the same reasons, astronauts would have a very hard life. Suppose the spaces can circulate at a speed of 29.999 km/h. In this case, the return trip to the Moon would spend three years on Earth, while two weeks would pass in the astronaut's life (including the stay on the surface of the Moon). After fifteen trips throughout his life, the astronaut would prove that his wife and children were his elders.
And of all this, in the end what?
That said, the TUE will have no impact on trains or our normal lifestyle. In addition, the effects described should not be taken literally, but as an approximation. In fact, days and years would be very different if there were c = 30 km/h. What you see is not a real summary of things, but a kind of twist and deformation. The higher the speed of an object, the more reddish it would appear, etc. But all these details follow us the same (the curious can go to the Critique of the abstract idea).
The idea we have to retain is that in nature there is a maximum speed, that of light, which produces strange or abnormal effects when we approach that speed. And for my part I would like to add the following idea: Although the footprints of the TUE are incredible, they are perfectly understandable. What is really surprising is that Einstein's theory depends only on a few scientists. I take root! We are not able to design the car engine, but we understand the operating bases. So be it with the TUE!
Critical idea summary
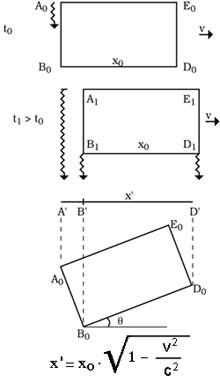
For this reason we cannot see the summary. Suppose a body A 0 B 0 D 0 E 0 moving with speed v. We are aligned with the direction of the movement, the B 0 D 0 being closer. As we know, what we know at a certain time is the rays that arrive simultaneously at that moment. Thus, as can be seen in the figure, the rays starting from A 0 to B 1 and D 1 will reach our eyes simultaneously. What we will see, therefore, as we explained in the article, is not only a summary B’D’, but also a hidden image of A 0 B 0 side A’B’. But that form of ‘A’B’D’ we see and the body with the angle q would be equal to the image rotated, as seen in the image. Therefore, when v is close to c we see that things turn and, at the same time, what is behind things is spectacular. |