Sous la relativité spéciale
Elhuyar. Science et Technique
Dans deux articles précédents, nous abordons des échelles de temps et des mesures mondiales en les comparant au quotidien. À cette occasion, nous aborderons la Théorie de la Relativité Spéciale.
Pourtant, bien qu'il y ait eu 86 ans depuis sa première connaissance de cette théorie, on le considère souvent comme quelque chose de caché, incompréhensible et sasimagique. Nous savons tous qui était Einstein: le sage qui a mis la science pieds en haut, le scientifique solitaire et génial qui savait beaucoup plus que quiconque, et beaucoup plus de sujets. Ainsi nous atténuons Einstein, en nous plaçant sur un piédestal, nous le rendons inaccessible et laissons sa théorie à quelques experts. Mais nous pouvons faire plus que de le connaître. En définitive, si nous croyons que les habitants du pôle sud ne bougent pas de mémoire, pourquoi ne pas croire ce que nous dit la Relativité Spéciale ?
Dans une simple articulation, nous n'ouvrons pas les yeux sur la nouvelle vérité, bien sûr, parce que pour cela il faut apprendre avec beaucoup d'effort, mais nous pouvons nous rapprocher des conclusions.
Par conséquent, nous ne montrerons aucune démonstration. En supposant ce que dit la théorie et les conséquences qui en découlent, nous changerons d'échelle pour que son essence influence notre vie quotidienne.
Théorie de la relativité spéciale
La Théorie de la Relativité d'Einstein se compose de deux paragraphes: le premier est la Théorie de la Relativité Spéciale (qui sera représenté avec l'abréviation TUE), dans laquelle on analyse les objets à vitesse constante et le second, la Théorie de la Relativité Générale (TGV), qui sera traitée dans un article ultérieur.
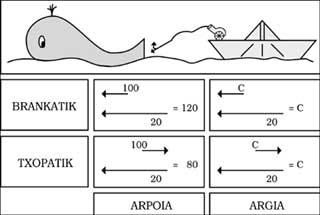
Pensons que nous sommes à la sentinelle d'un village de notre côte, explorant la mer ouverte, et que nous voyons un bateau naviguant à 20 km/h. À un moment donné, le baleinier projette le harpon de proue à 100 km/h. Nous verrons donc sortir le harpon à 120 km/h. En revanche, si le harpon est lancé depuis la chopa à égalité de conditions, nous le verrons de notre sentinelle à une vitesse de 80 km/h. Comme les mouvements du bateau et harpon sont de sens inverse, leurs vitesses ont tendance à être éliminés.
Jusqu'ici, il n'y a pas d'obstacle, mais maintenant nous allons mettre un foyer de lumière sur la place du canon harpon. Comme la vitesse de la lumière est de 300.000 km/s (indiqué par le symbole c), selon le même raisonnement supérieur, nous devrions voir les rayons de lumière de notre sentinelle à une vitesse de c+ 20 et c-20. Ce qui se passe n'est pas cela. En fait, nous verrons les rayons qui proviennent à la fois de la proue et de la chopa à la même vitesse ( c). De plus, indépendamment du mouvement du foyer de lumière, la vitesse de la lumière restera indéfiniment (voir figure 1).
L'expérience nous enseigne ce curieux comportement qui s'oppose à la logique. Et que la vitesse maximale possible est celle de la lumière, à savoir que la vitesse c ne peut pas être dépassé. Par conséquent, le concept (addition ou soustraction de vitesses) applicable dans des conditions spécifiques n'est pas applicable dans des conditions différentes. Cela signifie-t-il que parfois les formules (lois) applicables ne peuvent pas être appliquées à d'autres moments? Einstein a répondu non et a formulé la TUE comme suit:
- Les mêmes lois sont applicables dans toutes les conditions.
- La vitesse de la lumière est toujours constante (vide) et ne peut jamais être surmontée.
Pour compléter le postulat précédent, il faut fuir les anciennes formules de toujours et utiliser les nouvelles inventées par Lorentz (voir figure 2).
Cependant, ces nouvelles formules apportent une série de conséquences plus courantes.

Conclusions
Sans réaliser, en comprenant et en expliquant le monde que nous voyons, nous pensons qu'il y a des vitesses infinies. Par exemple, je l'ai vu quand cela est arrivé, mais pour cela la vitesse de la vue devrait être infinie, ou bien il faudra un temps pour parcourir l'espace depuis l'endroit où cela s'est passé jusqu'à mes yeux. Cependant, nous savons que la vitesse maximale est c, donc il n'y a pas de vitesses infinies. D'où nous pouvons tirer la première conclusion : certains pensent que les événements qui se produisent simultanément ne sont pas simultanés.
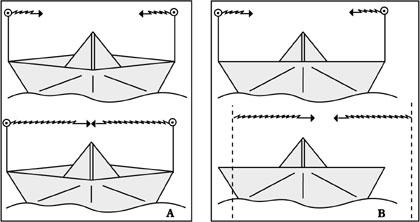
Par exemple, au centre du bateau il y a un pêcheur et comme les rayons qui vont par la proue et la chopa doivent parcourir la même distance, vous les verrez en même temps. Mais depuis notre sentinelle, nous verrons que pour que le rayon brancotique atteigne la moitié du bateau, il doit parcourir un chemin plus court que le chopatique (voir figure 3). Par conséquent, le brancanique arrive avant et nous ne les voyons pas à la fois !
Suivant un raisonnement similaire, nous verrons les objets qui se déplacent par rapport à nous plus courts que lorsqu'ils sont debout, et plus la vitesse est élevée, plus l'objet est court.
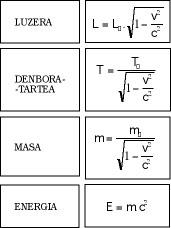
La troisième conclusion concerne le temps et est assez populaire. Selon cela, dans les corps en mouvement le temps passe plus lentement. Bien qu'il semble qu'il n'y ait aucune justification pour cela, c'est une conséquence directe des nouvelles formules. Enfin, il faut mentionner que la masse au repos des corps est plus légère que lorsqu'ils se déplacent et que l'énergie et la masse sont les mêmes. L'aspect mathématique de tout cela se reflète dans la figure 4.
Même si ces étranges conséquences peuvent être motivées par la théorie, quelqu'un pouvait penser que dans la vie quotidienne on n'a jamais vu cet effet. La vérité est qu'ils ont été vus. Car ils les voient tous les jours... ceux qui regardent les fractions de base. La raison en est la vitesse: ces effets ne se produisent que lorsque vous êtes près de la vitesse maximale en jeu (à commencer par les électrons et autres fractions), et que les vitesses que nous subissons et voyons dans notre vie sont si loin du maximum, nous ne percevons rien de spécial.
Ne désespérez pas. Pour que la TUE soit un peu plus proche, plus domestique et plus compréhensible, je vous propose un jeu : nous changerons la vitesse c.
Une journée de course
Pensons que la vitesse de la lumière est de c = 30 km/h. À cette condition, les effets du TUE seraient évidents dans notre vie. Pour commencer, nous ne pourrions jamais dépasser 30 km/h indépendamment de la ressource. Et quelles autres différences observerions-nous alors ?
Supposons que c'est dimanche et nous sommes allés à des courses de voiture. Nous nous sommes assis sur la tribune pour voir la course de là, mais il manque encore quelques minutes, donc nous allons analyser les caractéristiques de chaque détail. Nous voyons que la piste est une ligne droite de 2 km de longueur. A la sortie, trois voitures préparées de 3 m de long (voir figure 5). Finalement la course a commencé avec les voitures A et D assez égalées (29 et 29,9 km/h respectivement), mais le B a été lancé par panne ou ce qui est impossible (5 km/h).
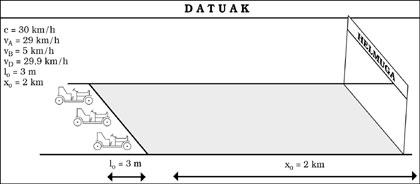
En passant devant nous, ces voitures de 3 m de long, debout, seront plus courtes et, plus vite nous irons, plus courtes nous paraîtront (voir figure 6). Cependant, une fois la course terminée, nous constatons que les trois d'entre elles ont une longueur de 3 m. Pendant ce temps, le gagnant sera D, bien sûr, les temps officiels à l'arrivée seront ceux de la figure 7.
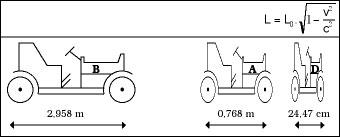
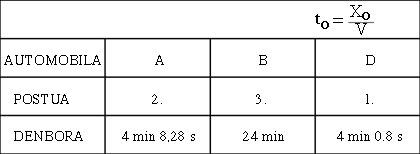
Si nous demandons aux pilotes, nous recevrions une image assez différente. Et bien que le critère du conducteur B coïncide plus ou moins avec le nôtre, les opinions de A et D seraient différentes. Pour A, par exemple, la piste serait de 512 m et défendrait que D avait 163 m (voir figure 8).
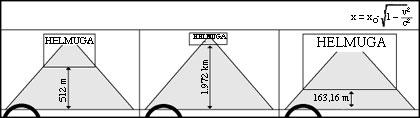
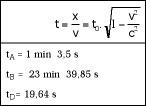
La même chose se passerait avec le temps. Nous pensons que si la distance entre A et D est de 7,5 secondes, ils considèrent qu'elle a été plus grande. Et c'est que nous avons pris 4 minutes pour aller du départ D à l'arrivée, mais elle n'a pris que 19 secondes pour faire la même chose (voir figure 9). Par conséquent, il est plus jeune que s'il s'était arrêté sur la gradation par la vitesse. C'est gagner du temps !
Le paradoxe des jumeaux
Mais ici apparaît une préoccupation. Plus la voiture est légère, plus nous l'avons vu et, symétriquement, les pilotes ont vu les objets de la piste plus vite c'est aller. En cela consiste précisément la relativité, c'est à dire, on pense que l'autre est plus court, mais l'autre croit que le premier est plus court, et ni l'un ni l'autre a raison, ou les deux ont, parce que les choses n'ont pas le seul aspect réel, mais selon le mouvement de l'observateur vont adopter différentes formes.
Et maintenant vient l'inquiétude que j'ai mentionné: nous avons vu les pilotes un peu plus jeunes, mais ils nous plus anciens et pas plus jeunes comme le ferait la symétrie de la relativité. Dans le cas du temps la relativité n'est-elle pas accomplie? Ce nœud est connu comme le paradoxe des jumeaux. La réponse est favorable au TUE. Voyons pourquoi.
Initialement, il a été commenté comme applicable dans les cas où il n'existe pas d'accélération TEE (vitesse constante). Si la piste se tient, nous pouvons considérer que les voitures se déplacent ou que les voitures se déplacent quand elles se tiennent, et l'un comme l'autre sont droites. Donc, nous verrons que le temps va plus lentement dans les voitures, et les pilotes verront que le temps va plus lentement sur la piste pendant que la vitesse des voitures reste constante. Ici se réalise la symétrie de la relativité. Cependant, les voitures doivent subir une accélération au moment de leur mouvement et un freinage final pour s'arrêter.
Dans ces deux moments spéciaux, la symétrie se brise et nous ne pouvons pas dire que ce qui bouge (piste ou voiture) est la même chose. Comme l'un d'eux (la voiture) a un mouvement spécial, le pilote sait qu'il ne se tient pas. La conséquence est que les pilotes et les pilotes sont d'accord pour répondre à la question d'où est le temps le plus lent.
Fou dans le monde
Et que se passerait-il dans un monde aussi bas ?
A 8’30 du matin, Jone et Mikel sont sortis de chez eux parce qu’ils ont un examen à l’Institut de Bilbao. Les deux laissent une matière à apprendre sur le chemin. Jone vit à Deusto. Par conséquent, il est sorti à pied et est venu dans environ une demi-heure, ayant terminé la matière. Mikel, de son côté, en résidant à Barakaldo, a pris à 8,30 le Train à Grande Vitesse (29,9 km/h) et est arrivé à 9 heures, mais n'a pas eu le temps de lire le début de la matière, car quelques secondes seulement ont passé dans sa vie interne.
Et pour les mêmes raisons, les astronautes auraient une vie très dure. Supposons que les espaces peuvent circuler à une vitesse de 29,999 km/h. Dans ce cas, le voyage aller-retour à la Lune passerait trois ans sur Terre, alors qu'ils passeraient deux semaines dans la vie de l'astronaute (y compris le séjour à la surface de la Lune). Après quinze voyages tout au long de sa vie, l'astronaute vérifierait que sa femme et ses enfants étaient ses aînés.
Et de tout cela, à la fin quoi ?
Cela dit, le TUE n'aura aucune incidence sur les trains ni sur notre mode de vie normal. En outre, les effets décrits ne doivent pas être pris littéralement, mais comme une approche. En fait, les jours et les années seraient très différents s'il y avait c = 30 km/h. Ce que vous voyez n'est pas un véritable résumé des choses, mais une sorte de tournage et de déformation. Plus la vitesse d'un objet est élevée, plus il apparaît rougeâtre, etc. Mais tous ces détails nous restent les mêmes (les curieux peuvent aller au tableau Critique de l'idée sommaire).
L'idée que nous devons retenir est que dans la nature il y a une vitesse maximale, celle de la lumière, ce qui produit des effets étranges ou anormaux lorsque nous nous approchons de cette vitesse. Et pour ma part, je voudrais ajouter l’idée suivante: Même si les traces du TUE sont incroyables, elles sont parfaitement compréhensibles. Ce qui est vraiment surprenant est que la théorie d'Einstein ne dépend que de quelques scientifiques. Enracinement ! Nous ne sommes pas en mesure de concevoir le moteur automobile, mais nous comprenons les bases de fonctionnement. C'est aussi avec le TUE !
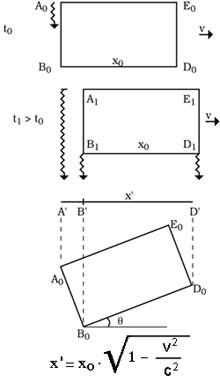
CRITIQUE IDÉE RÉSUMÉ
Pour cette raison, nous ne pouvons pas voir le résumé. Supposons un corps A 0 B 0 D 0 E 0 qui se déplace à la vitesse v. Nous sommes alignés avec la direction du mouvement, la B 0 D 0 étant plus proche. Comme nous le savons, ce que nous savons à un moment donné sont les rayons qui arrivent simultanément à ce moment. Ainsi, comme on peut l'apprécier dans la figure, les rayons qui partent de A 0 à B 1 et D 1 atteindront nos yeux simultanément. Ce que nous allons voir, donc, comme nous l’avons expliqué dans l’article, n’est pas seulement un résumé B’D’, mais aussi une image cachée de A 0 B 0 côté A’B’. Mais cette forme de ‘A’B’D’ que nous voyons et le corps avec l’angle q seraient égaux à l’image tournée, comme on le voit dans l’image. Par conséquent, quand v est proche de c nous voyons que les choses tournent et, en même temps, ce qui se cache derrière les choses est spectaculaire. |