¿Cómo operar? (I). Suma y resta
En números anteriores nos sumergimos en la historia de las cifras. Allí vimos los sistemas utilizados por el hombre. Lo que motivó a inventarse las cifras fue la necesidad de contar (y también las operaciones relacionadas con el cómputo). Pero, hasta que aparecía nuestro sistema, ¿cómo se resolvían las operaciones? Este artículo trata sobre esta pregunta. Las huellas encontradas nos permiten aproximarnos a la forma en que el hombre ha calculado.
Lo que le llevó a inventarse los números, como se ha dicho, fue la necesidad de contar. El conteo se hacía con el cuerpo. Aunque en algunos casos se utilizaban además de la mano otras partes del cuerpo (pies, brazos, cara, ...), se puede decir que la primera calculadora humana fue la mano. La mano, probablemente, creó las bases diez, cinco, doce y veinte. Además de contar manualmente, el hombre realizaba operaciones. En aquella época, debemos recordar que el ser humano no entendía ni conocía ningún número escrito. Sin embargo, era capaz de realizar varias multiplicaciones.
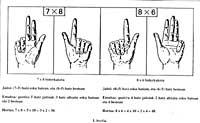
Por ejemplo, para multiplicar dos números entre 5 y 10, en una mano bajaban tantos dedos como un producto y la diferencia entre 5, en la otra el producto y el 5. El resultado se obtenía multiplicando el número de dedos rebajados en las dos manos por diez (de cabeza) y sumándose al producto de la cantidad de dedos sin bajar en ambas manos (Figura 1).
Esto tiene su verificación matemática: si x e y son números comprendidos entre 5 y 10, en una mano (x-5) descienden los dedos (y-5) y en la otra (y-5) y sin descender, en la primera hay 5 - (x-5) y en la segunda hay 5 - (y-5), siendo el número de dedos bajados (x-5) + (y-5). Realizando las operaciones mencionadas 10 [(x-5) + (y-5)] + [5 - (x-5)] . [5 - (y-5)] = 10 (x+y-10) + (10-x) . Tenemos (10-y) = 10x + 10y - 100 + 100 - 10x - 10y + xy = xy.
Una regla similar servía para multiplicar dos números entre 10 y 15 o dos números entre 15 y 20, etc.
Para multiplicar dos números entre 10 y 15, en cada mano se flexionaban tantos dedos como un producto y la diferencia entre 10; se multiplicaban por 10 el número de dedos agacados; luego se multiplicaban los dedos que habían bajado en dos manos y finalmente se sumaban los dos resultados y 100.
Todas estas sábanas tienen su verificación matemática, aunque el hombre de entonces no lo entienda.
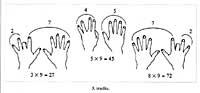
Como curiosidad indicaremos manualmente la tabla de multiplicación del número 9. Abriendo las dos manos delante de nosotros, de izquierda a derecha, después de dar a los dedos los valores 1, 2, 3, ..., agacharemos el dedo correspondiente al número que indica el otro producto que tiene como producto 9 y nos dará el resultado el número de dedos que quedan a cada lado de ese dedo; el lado izquierdo el decimal y el derecho la unidad (figura 3).
Pero vamos ahora a ver las primeras operaciones escritas. Antes de empezar, aclararemos que no vamos a usar las cifras actuales.
Suma
Es sin duda la operación más sencilla, tanto teórica como práctica. Veremos algunos ejemplos a lo largo de la historia de esta operación.
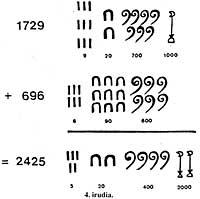
Para que los Egypti sumen dos números, como 1729 y 696, escribiendo sobre la canción
(Figura 4). Luego se recogían los mismos símbolos y se obtenía el resultado de sustituir 10 símbolos de un orden por uno de orden siguiente.
Otro ejemplo viene de la mano del abaco. En el ábaco, para unir dos números se escribían los dos a través de cantos, tras el bautizo, y el resultado aparecía después de hacer los resúmenes necesarios. Un ábaco especial, realizado en la arena mediante columnas, fue utilizado por hindúes que eran hábiles en el cálculo. En cada columna escribían un número, dejando la columna vacía para indicar cero o desorden. La suma se realizaba como el otro ábaco, pero sustituyendo los cantos por los números. De aquí viene el algoritmo que nosotros utilizamos ahora.
Sin embargo, los hindúes tenían otro algoritmo, el llamado retroceso. Esto (los números que se agrupaban por columnas comenzando por la izquierda) consistía en borrar la llevada cuando estaban las k (figura 5).

XVI. En 1540, Gemma Frisius creó un algoritmo. Escribía los números de mayor a menor y de arriba abajo y unía los números de cada columna. Los resultados parciales así obtenidos se escribían de derecha a izquierda y los recogían (figura 6).
Como puedes comprobar, la mayor diferencia entre los distintos algoritmos estaba en la expresión de resultados.
Resta
Lo que hace interesante esta operación es el caso en el que el restador es mayor que el minuendo, pero no vamos a entrar en él. El algoritmo de la sustracción no estaba estandarizado. Existen muchos métodos para realizar esta operación. Sin embargo, la idea de la demanda de formación es antigua y extendida. El método, o idea, fue utilizado por Fibonacci (Leonardo de Pisa) en 1202.
Sin embargo, vamos a traer el algoritmo de Columbia que evita pedir preparación. En el siguiente ejemplo se puede calcular la diferencia 8432-5976 según el algoritmo de Columbia: