How to operate? (I). Sum and subtraction
In previous numbers we dive into the history of the figures. There we saw the systems used by man. What motivated the figures to be invented was the need to count (and also operations related to computation). But, until our system appeared, how were the operations resolved? This article deals with this question. The footprints found allow us to approach the way in which man has calculated.
What led him to invent the numbers, as has been said, was the need to count. The count was made with the body. Although in some cases other parts of the body (feet, arms, face, ...) were used in addition to the hand, it can be said that the first human calculator was the hand. The hand, probably, created the bases ten, five, twelve and twenty. In addition to counting manually, the man carried out operations. At that time, we must remember that the human being did not understand or know any written numbers. However, he was able to perform several multiplications.
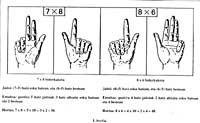
For example, to multiply two numbers between 5 and 10, in one hand they lowered as many fingers as a product and the difference between 5, in the other the product and 5. The result was obtained by multiplying the number of fingers lowered in the two hands by ten (head) and adding to the product of the number of fingers without lowering in both hands (Figure 1).
This has its mathematical verification: if x e and are numbers between 5 and 10, in one hand (x-5) descend fingers (y-5) and in the other (y-5) and without descending, in the first there are 5 - (x-5) and in the second there are 5 - (y-5), being the number of lowered fingers (x-5) + (y-5). Performing the mentioned operations 10 [(x-5) + (y-5)] + [5 - (x-5)] . [5 - (y-5)] = 10 (x+y-10) + (10-x). We have (10-y) = 10x + 10y - 100 + 100 - 10x - 10y + xy = xy.
A similar rule served to multiply two numbers between 10 and 15 or two numbers between 15 and 20, etc.
To multiply two numbers between 10 and 15, in each hand were flexed as many fingers as a product and the difference between 10; the number of fingers were multiplied by 10; then the fingers that had been lowered in two hands multiplied and finally the two results were added and 100.
All these sheets have their mathematical verification, although the man then does not understand it.
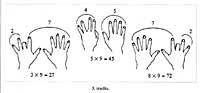
As curiosity we will manually indicate the multiplication table of the number 9. Opening the two hands in front of us, from left to right, after giving the fingers the values 1, 2, 3, ..., we will bend the finger corresponding to the number that indicates the other product that has as a product 9 and will give us the result the number of fingers left on each side of that finger; the left side the decimal and the right the unit (figure 3).
But let's now see the first written operations. Before we start, we will clarify that we will not use the current figures.
Sum of sum
It is undoubtedly the simplest operation, both theoretical and practical. We will see some examples throughout the history of this operation.
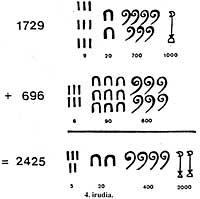
For the Egypti to add two numbers, such as 1729 and 696, writing about the song
(Figure 4). Then the same symbols were collected and the result of substituting 10 symbols of an order by one of the following order was obtained.
Another example comes from the hand of the abaco. In the abacus, to join two numbers the two were written through songs, after baptism, and the result appeared after making the necessary summaries. A special abacus, made in the sand by columns, was used by Hindus who were skilled in calculus. In each column they wrote a number, leaving the column empty to indicate zero or disorder. The sum was made as the other abacus, but replacing the songs with the numbers. From here comes the algorithm that we use now.
However, the Hindus had another algorithm, the so-called decline. This (the numbers grouped by columns starting from the left) consisted of erasing the lead when the k were (figure 5).

XVI. In 1540, Gemma Frisius created an algorithm. He wrote the numbers from greater to smaller and from top to bottom and joined the numbers of each column. The partial results thus obtained were written from right to left and collected (Figure 6).
As you can see, the biggest difference between the different algorithms was in the expression of results.
Subtraction of Resta
What makes this operation interesting is the case in which the restator is greater than the minutes, but we will not enter it. The algorithm of the subtraction was not standardized. There are many methods to perform this operation. However, the idea of the demand for training is ancient and widespread. The method, or idea, was used by Fibonacci (Leonardo de Pisa) in 1202.
However, we will bring the Columbia algorithm that avoids asking for preparation. In the following example you can calculate the difference 8432-5976 according to the Columbia algorithm: