Hasiera »   Erreportajeak »   Bizikleta

Bicicleta

• Zabaldu:
• Twitter
• Facebook
• Emaila

Nada máis chegar a primavera, o sangue comeza a quentarse; sentimos que estamos a rexuvenecer. A tempada ciclista acaba de empezar ou está a piques de empezar. Nós tamén saímos da nosa cámara e despois de limpala e preparala, estamos a piques de saír ás estradas. Queremos estrear a bicicleta de montaña que nos deron este ano; cambiamos o piñón e o prato á bicicleta vella e estamos á espera da ocasión paira probala.

Polo menos dúas cousas temos medo dos ciclistas: ao tráfico nas estradas e a nós mesmos (... serei capaz? ). Paira acabar co primeiro é imprescindible concienciar aos condutores. A iso dedícanse as asociacións de ciclistas. O feito de que en Euskal Herria haxa tanta afección fai que haxa tantos accidentes. Nas grandes cidades e pobos predominan os automóbiles. Salvo en moi poucos casos, non hai vías vermellas, nin entre cidades, pobos nin pobos. E o que é máis grave, non existe una política de fomento do uso da bicicleta.

En canto ao segundo, a primeira lei da bicicleta, calquera que sexa o sentido de circulación, di que sempre haberá vento en contra e pendente. De feito, as estradas están concibidas paira circular automóbiles e os automóbiles elevan as costas de forma fácil e correcta. Os ciclistas, pola contra, teñen que facer esforzos duros, aínda que cos avances que se produciron nos últimos anos no ciclismo tiveron un gran apoio.

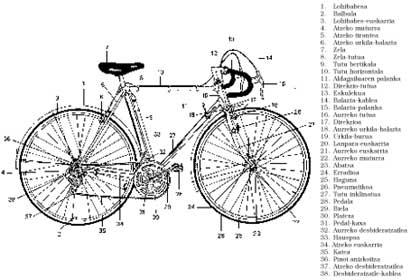
As bicicletas actuais teñen entre cinco e seis piñones e dous ou tres pratos, os cambiadores están no manillar, hai manillares especiais para que o corpo teña una aerodinámica adecuada, rodas tipo lentella, etc. Con todo, o maior avance foi a transmisión en cadea.

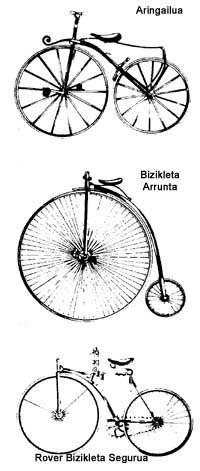
Este último avance non é do último período, xa que ten máis dun século. Até 1885, ano no que Starley puxo ao seu “Rover Safety Bicycle” a transmisión en cadea, os pedais estaban unidos á roda motriz, é dicir, todas as bicicletas servíanse da transmisión directa. En consecuencia, por cada volta de pedais a bicicleta avanzaba a lonxitude da circunferencia da roda e o desenvolvemento da bicicleta dependía da roda motriz. Con todo, mesmo con grandes rodas motrices o desenvolvemento era baixo comparándoo coas bicicletas máis modernas.

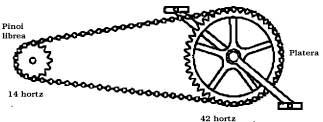
Paira calcular o factor de relación da transmisión en cadea dunha bicicleta basta con calcular o cociente entre o número de dentes do prato e o piñón. Por exemplo, se o prato ten 48 dentes e o piñón 12 dentes, o factor de transmisión en cadea é:

Paira comprender mellor hai que ver que toda una volta do prato (pedal) adianta 48 niveis da cadea, o que fai que o piñón vire catro veces (porque ten 12 dentes).

Nunha bicicleta cun prato de 42 dentes e un piñón de 14 dentes, una volta completa do prato virará o piñón tres veces. Así que a roda traseira tamén dará tres voltas. Dado que a roda da bicicleta común ten un diámetro de 69 cm, una volta ao prato adiantará a bicicleta 3 x 69 x p = 650,30 cm. Rodas de bicicletas antigas de 3 x 69 x p = 650,30 cm de lonxitude, ou de 3 x 69 = 207 cm de diámetro, paira conseguir o mesmo avance que farían falta. Como se pode adiviñar, paira poder circular neste tipo de bicicleta sería necesario dispor dunha perna de aproximadamente 130 cm.

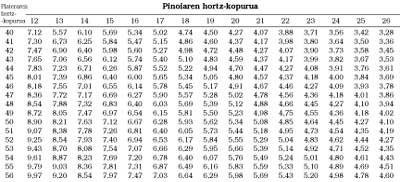
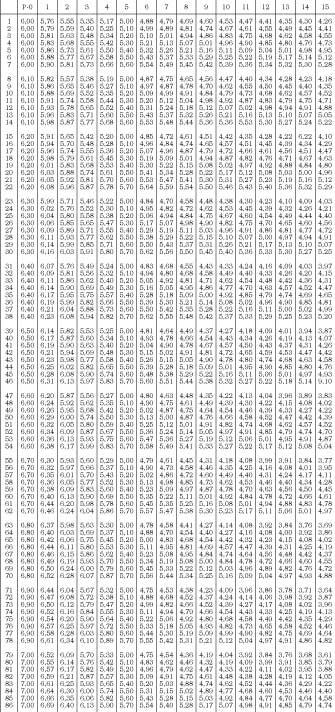
Na seguinte táboa podemos ver os desenvolvementos de bicicletas. (Táboa 1).

Cando José Meifret rompeu a marca mundial de velocidade en bicicleta (superando os 230 km/h) utilizou un factor de transmisión de 10 entre prato e piñón (un paliador ou un velocípedo necesitaría una roda de 7 m de diámetro). Cantos pratos e piñones podía utilizar? Poderíase conseguir un maior desenvolvemento mediante este método?

Na televisión vimos aos ciclistas en subida. O primeiro parece estar lento e canso. O segundo, con todo, rápido e forte, crendo que atrapará ao primeiro. Ao final démonos conta de que o primeiro ten máis vantaxe. Pero, como é posible? Si, así é e ten una explicación sinxela. O primeiro utilizou máis desenvolvemento que o segundo, é dicir, avanzou máis. Paira un maior desenvolvemento necesítase un prato máis grande, polo que necesitou máis forza paira mover o pedal e por iso parecía canso. Pola contra, o segundo moveu máis facilmente os pratos máis pequenos, pero se adiantou menos.

Trataremos de responder a dúas preguntas. A primeira é que desenvolvemento hai que utilizar nas pendentes? A resposta non será exacta, xa que depende de persoas, bicicletas, tempo, etc. Con todo, existe una táboa que nos pode axudar (Táboa 2). Paira utilizar a táboa son necesarios dous datos: o desenvolvemento que se utiliza no computador e outro. Na citada táboa móstranse os desenvolvementos utilizados na meseta na columna p = 0. Por exemplo, se lle vén ben o desenvolvemento en orde de 6,4 e en pendentes de 5% o desenvolvemento de 5,4 (fila 35), o desenvolvemento que lle corresponde paira afrontar a pendente do 12% será de 4,79. Agora imos á táboa principal, buscamos os máis próximos ao 4,79 e atopamos 40x18, 43x19, 45x20, 47x21, 49x22, 52x23, 54x24, 56x25.

A segunda pregunta é cal das opcións é a máis adecuada? Una vez máis a resposta non é exacta. As opcións con máis dentes teñen as seguintes vantaxes:

• a forza transversal na cadea é menor;
• a torsión da cadea tamén é menor, aproveitando mellor os esforzos sobre os dentes do piñón;
• a forma de pedalear é máis redondeada, menos ríxida.

As desvantaxes son:

• alargar a lonxitude e o esforzo da cadea;
• maior peso do sistema de transmisión.

En xeral, as combinacións con maior número de dentes serán seleccionadas paira a sobremesa. En percorridos inclinados e duros, os menos dentes. O maior rendemento mecánico obtense con pratos de 46-47 dentes. Na estrada non se recomenda menos ou máis de 50.

Paira coñecer o desenvolvemento que lle corresponde, o ciclista debe controlar a velocidade e a cadencia que quere levar (é dicir, o número de revolucións por minuto que dá aos pedais). Estes dous datos proporcionarannos o desenvolvemento a seleccionar mediante a seguinte fórmula:

Por exemplo, se se quere alcanzar una velocidade de 24 km/h utilizando una cadencia de 75 r.p.m., débese elixir un desenvolvemento de 5,3 m. Vendo a táboa 1, 40x16, 42x17, 45x18, ...

Catro ou cinco cores J. Duoandikoetxea informoume que o dato que dixen sobre o estado do teorema no artigo de xaneiro, denominado catro ou cinco cores, é moi obsoleto. Dicía: A situación actual do problema (que eu saiba) é: Comprobouse que se cumpre en todos os mapas que non teñen máis de 38 comarcas. J. Duoandikoetxea expón: C. 1976 Appel e W. Haken demostrou o teorema, pero utilizando un camiño non habitual, o computador. O traballo realizado polo computador non se pode realizar manualmente. Foi un feito interesante, xa que supuxo un debate con eles. ... O debate non é si o teorema é real ou non. Podemos facer a mesma pregunta que Davis e Hersch: “por que crer ao computador?”. Pero, a pesar de que paira os nosos matemáticos “clásicos” non me gusta recoñecer que iso é una demostración, non creo que en diante ninguén teña a esperanza de demostrar que o teorema é falso. Posto que non é posible realizar manualmente o mesmo traballo que realizou o computador, se algunha vez realizásese una demostración clásica habería que facelo aplicando outras ideas. E iso é o que máis esperamos paira o futuro. A ver se o fai alguén. Grazas a Jabi pola súa explicación.

Nota: Paira ver ben as imaxes accede ao pdf.