Hasiera »   Erreportajeak »   Bizikleta

Bicicleta

• Zabaldu:
• Twitter
• Facebook
• Emaila

Nada más llegar la primavera, la sangre comienza a calentarse; sentimos que estamos rejuveneciendo. La temporada ciclista acaba de empezar o está a punto de empezar. Nosotros también salimos de nuestra cámara y después de limpiarla y prepararla, estamos a punto de salir a las carreteras. Queremos estrenar la bicicleta de montaña que nos han dado este año; hemos cambiado el piñón y el plato a la bicicleta vieja y estamos a la espera de la ocasión para probarla.

Al menos dos cosas tenemos miedo de los ciclistas: al tráfico en las carreteras y a nosotros mismos (... ¿seré capaz? ). Para acabar con el primero es imprescindible concienciar a los conductores. A ello se dedican las asociaciones de ciclistas. El hecho de que en Euskal Herria haya tanta afición hace que haya tantos accidentes. En las grandes ciudades y pueblos predominan los automóviles. Salvo en muy pocos casos, no hay vías rojas, ni entre ciudades, pueblos ni pueblos. Y lo que es más grave, no existe una política de fomento del uso de la bicicleta.

En cuanto al segundo, la primera ley de la bicicleta, cualquiera que sea el sentido de circulación, dice que siempre habrá viento en contra y pendiente. De hecho, las carreteras están concebidas para circular automóviles y los automóviles elevan las cuestas de forma fácil y correcta. Los ciclistas, por el contrario, tienen que hacer esfuerzos duros, aunque con los avances que se han producido en los últimos años en el ciclismo han tenido un gran apoyo.

Las bicicletas actuales tienen entre cinco y seis piñones y dos o tres platos, los cambiadores están en el manillar, hay manillares especiales para que el cuerpo tenga una aerodinámica adecuada, ruedas tipo lenteja, etc. Sin embargo, el mayor avance ha sido la transmisión en cadena.

Este último avance no es del último periodo, ya que tiene más de un siglo. Hasta 1885, año en el que Starley puso a su “Rover Safety Bicycle” la transmisión en cadena, los pedales estaban unidos a la rueda motriz, es decir, todas las bicicletas se servían de la transmisión directa. En consecuencia, por cada vuelta de pedales la bicicleta avanzaba la longitud de la circunferencia de la rueda y el desarrollo de la bicicleta dependía de la rueda motriz. Sin embargo, incluso con grandes ruedas motrices el desarrollo era bajo comparándolo con las bicicletas más modernas.

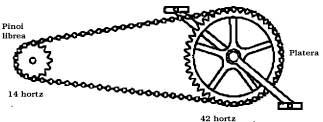
Para calcular el factor de relación de la transmisión en cadena de una bicicleta basta con calcular el cociente entre el número de dientes del plato y el piñón. Por ejemplo, si el plato tiene 48 dientes y el piñón 12 dientes, el factor de transmisión en cadena es:

Para comprender mejor hay que ver que toda una vuelta del plato (pedal) adelanta 48 niveles de la cadena, lo que hace que el piñón gire cuatro veces (porque tiene 12 dientes).

En una bicicleta con un plato de 42 dientes y un piñón de 14 dientes, una vuelta completa del plato girará el piñón tres veces. Así que la rueda trasera también dará tres vueltas. Dado que la rueda de la bicicleta común tiene un diámetro de 69 cm, una vuelta al plato adelantará la bicicleta 3 x 69 x p = 650,30 cm. Ruedas de bicicletas antiguas de 3 x 69 x p = 650,30 cm de longitud, o de 3 x 69 = 207 cm de diámetro, para conseguir el mismo avance que harían falta. Como se puede adivinar, para poder circular en este tipo de bicicleta sería necesario disponer de una pierna de aproximadamente 130 cm.

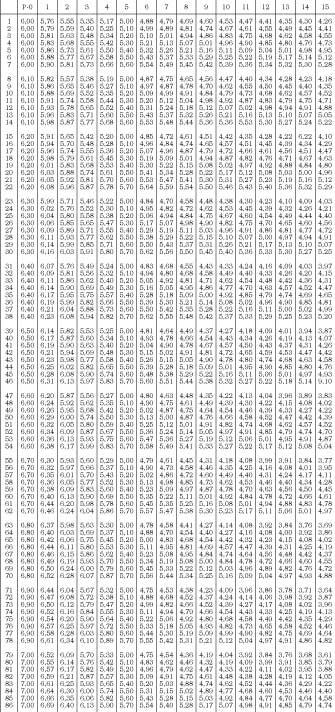
En la siguiente tabla podemos ver los desarrollos de bicicletas. (Tabla 1).

Cuando José Meifret rompió el récord mundial de velocidad en bicicleta (superando los 230 km/h) utilizó un factor de transmisión de 10 entre plato y piñón (un paliador o un velocípedo necesitaría una rueda de 7 m de diámetro). ¿Cuántos platos y piñones podía utilizar? ¿Se podría conseguir un mayor desarrollo mediante este método?

En la televisión hemos visto a los ciclistas en subida. El primero parece estar lento y cansado. El segundo, sin embargo, rápido y fuerte, creyendo que atrapará al primero. Al final nos hemos dado cuenta de que el primero tiene más ventaja. Pero, ¿cómo es posible? Sí, así es y tiene una explicación sencilla. El primero ha utilizado más desarrollo que el segundo, es decir, ha avanzado más. Para un mayor desarrollo se necesita un plato más grande, por lo que ha necesitado más fuerza para mover el pedal y por eso parecía cansado. Por el contrario, el segundo ha movido más fácilmente los platos más pequeños, pero se ha adelantado menos.

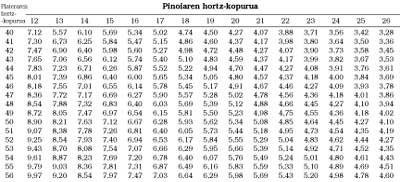
Trataremos de responder a dos preguntas. La primera es ¿qué desarrollo hay que utilizar en las pendientes? La respuesta no será exacta, ya que depende de personas, bicicletas, tiempo, etc. Sin embargo, existe una tabla que nos puede ayudar (Tabla 2). Para utilizar la tabla son necesarios dos datos: el desarrollo que se utiliza en el ordenador y otro. En la citada tabla se muestran los desarrollos utilizados en la meseta en la columna p = 0. Por ejemplo, si le viene bien el desarrollo en orden de 6,4 y en pendientes de 5% el desarrollo de 5,4 (fila 35), el desarrollo que le corresponde para afrontar la pendiente del 12% será de 4,79. Ahora vamos a la tabla principal, buscamos los más cercanos al 4,79 y encontramos 40x18, 43x19, 45x20, 47x21, 49x22, 52x23, 54x24, 56x25.

La segunda pregunta es ¿cuál de las opciones es la más adecuada? Una vez más la respuesta no es exacta. Las opciones con más dientes tienen las siguientes ventajas:

• la fuerza transversal en la cadena es menor;
• la torsión de la cadena también es menor, aprovechando mejor los esfuerzos sobre los dientes del piñón;
• la forma de pedalear es más redondeada, menos rígida.

Las desventajas son:

• alargar la longitud y el esfuerzo de la cadena;
• mayor peso del sistema de transmisión.

En general, las combinaciones con mayor número de dientes serán seleccionadas para el postre. En recorridos inclinados y duros, los menos dientes. El mayor rendimiento mecánico se obtiene con platos de 46-47 dientes. En carretera no se recomienda menos o más de 50.

Para conocer el desarrollo que le corresponde, el ciclista debe controlar la velocidad y la cadencia que quiere llevar (es decir, el número de revoluciones por minuto que da a los pedales). Estos dos datos nos proporcionarán el desarrollo a seleccionar mediante la siguiente fórmula:

Por ejemplo, si se quiere alcanzar una velocidad de 24 km/h utilizando una cadencia de 75 r.p.m., se debe elegir un desarrollo de 5,3 m. Viendo la tabla 1, 40x16, 42x17, 45x18, ...

Cuatro o cinco colores J. Duoandikoetxea me ha informado que el dato que dije sobre el estado del teorema en el artículo de enero, denominado cuatro o cinco colores, es muy obsoleto. Decía: La situación actual del problema (que yo sepa) es: Se ha comprobado que se cumple en todos los mapas que no tienen más de 38 comarcas. J. Duoandikoetxea expone: C. 1976 Appel y W. Haken demostró el teorema, pero utilizando un camino no habitual, el ordenador. El trabajo realizado por el ordenador no se puede realizar manualmente. Fue un hecho interesante, ya que supuso un debate con ellos. ... El debate no es si el teorema es real o no. Podemos hacer la misma pregunta que Davis y Hersch: “¿por qué creer al ordenador?”. Pero, a pesar de que para nuestros matemáticos “clásicos” no me gusta reconocer que eso es una demostración, no creo que en adelante nadie tenga la esperanza de demostrar que el teorema es falso. Puesto que no es posible realizar manualmente el mismo trabajo que ha realizado el ordenador, si alguna vez se realizara una demostración clásica habría que hacerlo aplicando otras ideas. Y eso es lo que más esperamos para el futuro. A ver si lo hace alguien. Gracias a Jabi por su explicación.

Nota: Para ver bien las imágenes accede al pdf.