Hasiera »   Erreportajeak »   Bizikleta

Bicycle

• Zabaldu:
• Twitter
• Facebook
• Emaila

As soon as spring arrives, the blood begins to warm; we feel that we are rejuvenating. The cycling season has just begun or is about to begin. We also leave our camera and after cleaning and preparing it, we are about to go on the roads. We want to premiere the mountain bike that we have been given this year; we have changed the pinion and plate to the old bike and we are waiting for the occasion to try it.

At least two things are afraid of cyclists: traffic on the roads and ourselves (... will I be able? ). To end the first is essential to raise awareness of drivers. Cyclist associations are dedicated to this. The fact that there is so much fondness in Euskal Herria makes there so many accidents. Cars predominate in large cities and towns. Except in very few cases, there are no red routes, neither between cities, towns or villages. And more seriously, there is no policy to encourage the use of bicycles.

As for the second, the first law of the bicycle, whatever the sense of circulation, says that there will always be wind against and slope. In fact, roads are designed to drive cars and cars lift the slopes easily and correctly. Cyclists, on the contrary, have to make hard efforts, although with the advances that have occurred in recent years in cycling have had great support.

The current bikes have between five and six pinions and two or three plates, the changers are on the handlebar, there are special handlebars for the body to have proper aerodynamics, lentil type wheels, etc. However, the biggest advance has been chain transmission.

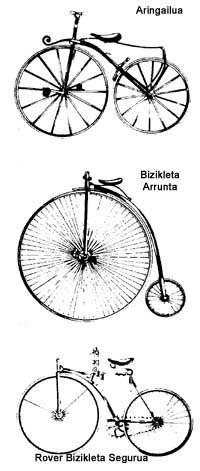
This last advance is not of the last period, since it has more than a century. Until 1885, the year in which Starley put his “Rover Safety Bicycle” on the chain drive, the pedals were attached to the drive wheel, that is, all the bicycles used direct transmission. Consequently, for every turn of pedals the bicycle advanced the length of the wheel circumference and the development of the bicycle depended on the driving wheel. However, even with large drive wheels the development was low compared to the most modern bikes.

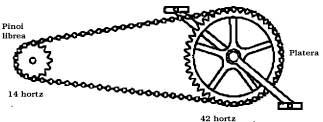
To calculate the ratio factor of the chain drive of a bicycle, simply calculate the ratio between the number of teeth of the plate and the pinion. For example, if the plate has 48 teeth and the pinion 12 teeth, the chain drive factor is:

To better understand, one must see that a whole turn of the plate (pedal) advances 48 levels of the chain, which makes the pinion turn four times (because it has 12 teeth).

On a bike with a 42 tooth plate and a 14-tooth sprocket, a full turn of the plate will turn the sprocket three times. So the rear wheel will also take three turns. Since the wheel of the common bicycle has a diameter of 69 cm, a turn to the plate will advance the bike 3 x 69 x p = 650,30 cm. Antique bicycle wheels 3 x 69 x p = 650.30 cm in length, or 3 x 69 = 207 cm in diameter, to achieve the same advance that would be needed. As you can guess, to be able to circulate in this type of bicycle it would be necessary to have a leg of approximately 130 cm.

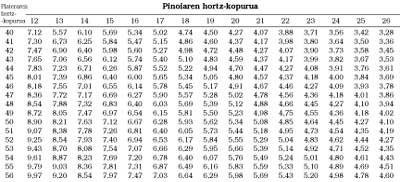
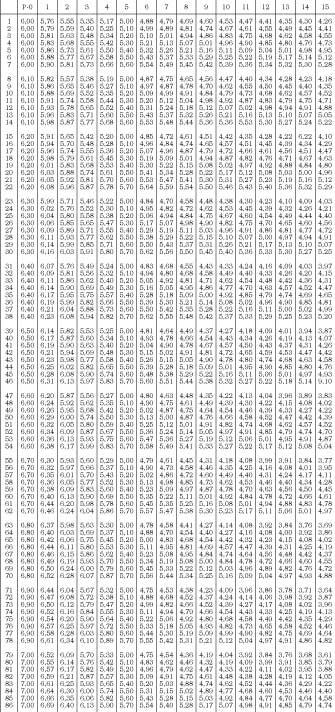
In the table below we can see the bike developments. (Table 1).

When José Meifret broke the world bike speed record (exceeding 230 km/h) he used a transmission factor of 10 between plate and pinion (a pallet or a speedopedal would need a wheel of 7 m in diameter). How many dishes and pinions could I use? Could greater development be achieved through this method?

On TV we have seen cyclists on the rise. The first seems to be slow and tired. The second, however, fast and strong, believing that it will catch the first. In the end we realized that the first has more advantage. But how is it possible? Yes, it is and has a simple explanation. The first has used more development than the second, that is, has advanced more. For further development a larger plate is needed, so it has needed more strength to move the pedal and so it seemed tired. On the contrary, the second more easily moved the smaller dishes, but less advanced.

We will try to answer two questions. The first is what development should be used on slopes? The answer will not be accurate, as it depends on people, bicycles, time, etc. However, there is a table that can help us (Table 2). To use the table two data are necessary: the development that is used on the computer and another. The mentioned table shows the developments used in the plateau in column p = 0. For example, if you have good development in order of 6.4 and on slopes of 5% the development of 5.4 (row 35), the development that corresponds to face the slope of 12% will be 4.79. Now we go to the main table, we look for those closest to 4.79 and find 40x18, 43x19, 45x20, 47x21, 49x22, 52x23, 54x24, 56x25.

The second question is which of the options is the most suitable? Again the answer is not accurate. Options with more teeth have the following advantages:

• the transverse force in the chain is smaller;
• the torsion of the chain is also smaller, making better use of the efforts on the sprocket teeth;
• the pedaling shape is more rounded, less rigid.

The disadvantages are:

• lengthening the length and effort of the chain;
• higher transmission system weight.

In general, combinations with more teeth will be selected for dessert. On inclined and hard routes, the least teeth. The highest mechanical performance is obtained with dishes of 46-47 teeth. On road is not recommended less or more than 50.

To know the development that corresponds to him, the cyclist must control the speed and cadence that he wants to carry (that is, the number of revolutions per minute that gives to the pedals). These two data will provide us with the development to select using the following formula:

For example, if you want to reach a speed of 24 km/h using a cadence of 75 r.p.m., you should choose a development of 5.3 m. Viewing table 1, 40x16, 42x17, 45x18, ...

Four or five colors J. Duoandikoetxea has informed me that the data I said about the state of the theorem in the January article, called four or five colors, is very obsolete. He said: The current situation of the problem (as far as I know) is: It has been proven to be true on all maps with no more than 38 regions. J. Duoandikoetxea exhibits: C. 1976 Appel and W. Haken demonstrated the theorem, but using an unusual path, the computer. The work done by the computer cannot be done manually. It was an interesting fact, as it was a debate with them. ... The debate is not whether the theorem is real or not. We can ask the same question as Davis and Hersch: “Why believe the computer?” But, even though for our “classical” mathematicians I don’t like to recognize that this is a demonstration, I don’t think that henceforth anyone hopes to prove that the theorem is false. Since it is not possible to manually perform the same work that the computer has done, if ever a classic demonstration was made it would be necessary to do so applying other ideas. And that is what we expect most for the future. See if someone does. Thank you to Jabi for your explanation.

Note: To see the images well go to the pdf.