Fisika: 50 urte aurrerago, zer?
“Teknologia kuantikoak erabiliko ditugu ikertzeko eta komunikatzeko”
Nire eremuan, hemendik 50 urtera, teknologia kuantikoak izango dira nagusi. Horiek izango dira ikertzeko eta komunikatzeko erabiliko ditugun teknologiak. Egoera korapilatsuen propietateetan oinarritzen diren teknologiak dira. Baina zer dira korapilatutako egoera horiek, eta non gaude momentu honetan? Has gaitezen hasieratik…
Mekanika kuantikoak gure teoria zientifikoetatik arrakastatsuena eta aldi berean misteriotsuena izatearen ospe bitxia du. 1900etik 1920ra bitarteko aldi nabarmen batean garatu zen, eta gaur egungo formalismoa, berriz, 1920ko hamarkadaren amaieran. Handik aurrera, fisikariek arrakasta handia izan zuten mekanika kuantikoa aplikatuz naturaren oinarrizko partikulak eta indarrak ulertzeko, eta partikulen fisikaren eredu estandarra eratzera iritsi ziren. Aldi berean, fisikariek berdin-berdin arrakasta handia izan zuten mekanika kuantikoa aplikatzean, gure munduko fenomeno-sorta harrigarria ulertzeko, polimeroetatik erdieroaleetara, superfluidoetatik supereroaleetaraino. Baina, garapen horiek mundu naturalaren ulermena sakonki aurreratu zuten arren, mekanika kuantikoaren ulermena apur bat bakarrik hobetu zuten.
Teknologia kuantikoen oinarria: korapilatze kuantikoa
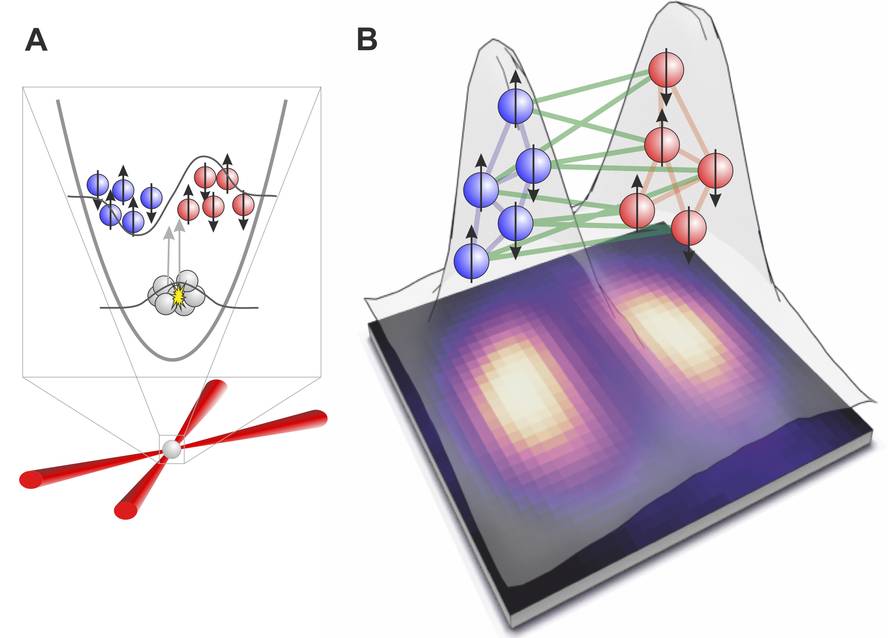
Hemen arituko naiz mekanika kuantikoa konputazio kuantikora aplikatzeaz, eta, horretarako, haren oinarri teorikoa aurkeztu behar dugu: korapilatutako egoerak. Egoera korapilatuen historia Einstein mekanika kuantikoaren oinarriekin ados ez egotearekin hasi zen, EPR paradoxa deritzona formulatu zenean, hain zuzen ere. Elkarrekin korapilatuta dauden bi partikularen eredua aztertzen zuen paradoxak, Einstein tematuta baitzegoen hori ukatu nahian. Gaur egun, korapilatze kuantikoa fisika kuantikoaren printzipio nagusietako bat da. Korapilatze kuantikoak esan nahi du partikula anitz elkarrekin nolabait lotuta daudela, eta bakarra balira bezala jokatzen dutela. Hala, partikula baten egoera kuantikoa neurtzean, beste partikulen egoera kuantiko posibleak ezagutu eta zehaztu ditzakegu.
Konexio hau ez da partikulen kokapen espazialaren araberakoa. Nahastutako partikulak milaka milioi kilometroz bereizten badituzu ere, partikula bat aldatzeak bestean aldaketa eragingo du. Einsteinentzat, hori paradoxa bat zen, itxuraz bi partikulen arteko komunikazio bat baitakar, argiarena baino abiadura handiagoan gertatu beharrekoa; eta hori gatazkan dago Albert Einsteinen beraren erlatibitatearen teoriarekin. Hala ere, geroago frogatu zen Einsteinen interpretazioa okerra zela, partikulak ez direlako mugitzen. Nahiz eta badirudien korapilatze kuantikoaz informazioa berehala transmititzen dela, ez du argiaren abiadura klasikoa urratzen, berez ez baitago “mugimendurik”. Mekanika kuantikoa ukatu nahian, Einsteinek korapilatzearen ideia asmatu zuen.
Imajinatu zein izan zitekeen ideia honen potentzial teknologikoa, egoera korapilatuak kontrolpean izatea lortuz gero: partikula batez, oso urruti dagoen beste batean eragin daiteke. Hala eta guztiz ere, hamarkada mordo bat pasatu behar izan zen korapilatze kuantikoren aplikazioak aurkitzeko.
Galdera berriak
1970eko eta 1980ko hamarkadetan, mekanika kuantikoari buruz pentsatzen zuten modua aldatzen hasi zen. Ikerlari batzuk inspiratu ziren beren buruari galdetuz ea informatikaren eta informazioaren oinarrizko galdera batzuk sistema kuantikoen azterketan aplika litezkeen. Lehen, sistema kuantikoak fenomeno naturalak azaltzeko bakarrik erabiltzen ziren; ikerlari hauek frogatu zuten sistema kuantikoak edozein aplikaziotarako ere diseinatu ahal zirela. Ikuspegi-aldaketa txiki bat dirudi, baina ondorioak sakonak izan ziren. Jada ez da mundu kuantikoa behatzen, baina horren ordez mundu kuantikoa sor daiteke gure gustura.
Alde batetik, mekanika kuantikoaren oinarriekiko interesa berpiztu zen, eta, beste aldetik, galdera berri asko sortu ziren fisika, informatika eta informazioaren teoriaren arloak konbinatuz. Horien artean daude honelako galderak: zein dira espazioaren eta denboraren oinarrizko muga fisikoak, egoera kuantikoa eraikitzeko?; zenbat denbora eta espazio behar da eragiketa dinamiko jakin baterako?; zergatik gertatzen da hain zaila sistema kuantikoak ulertzea eta simulatzea sistema klasikoak erabiliz?
Lau mugarri
Harrezkero, aurrerapen asko izan dira. Beharbada aurrerapenik ikusgarriena esperimentuen arloan izan da. Eskala handiko ordenagailu kuantikoak eraikitzeko urte asko falta dira oraindik, baina aurrerapen handiak egin dira. Zirkuitu supereroaleak erabili dira bi qubiteko* algoritmo kuantiko sinpleak ezartzeko, eta hiru qubitez osatutako sistemak ia eskura daude. Spin nuklearretan eta fotoi bakarrean oinarritutako qubitak erabili dira, hurrenez hurren, akats kuantikoen zuzenketa eta simulazio kuantikorako printzipioaren inplementazioa frogatzeko. Baina guztietatik aurrerapen ikus-garriena ioi-sistemekin egin da. Harrapatutako ioiak oinarrizko komunikazio kuantikoen basea erakusteko ere erabili dira, errore kuantikoen zuzenketa eta teleportazio kuantikoa barne.
Bigarren aurrerapena izan da nola inplementatu ahal diren algoritmo kuantikoak ordenagailu kuantikoetan. Harrigarriro, konputazio kuantikoa besterik gabe inplementatu daiteke qubit bakarreko sekuentzia neurtuz; zenbat, noiz eta nola neurtzen diren qubitak inplementazio ezberdinak emango dizkigu. Hau nabarmena da: egoera kuantiko finko bat ematen dizute, eta gero kalkulu kuantikoa qubit indibidualei modu egokian “begiratuz” lortzen da.
Hirugarren aurrerapena sistema kuantikoak klasikoki simulatzearen ariketa izan da. Sistema kuantikoak askotan ordenagailu klasiko konbentzionaletan simulatzea zaila dela dirudi, izatez konputazio-muga dezente dugu ordenagailu klasikoekin. Baina 2000ko hamarkadan ikasi dugu zein sistema kuantiko simulatzen diren erraz eta zein diren simulatzen zailak. Algoritmo burutsuak garatu dira antzina simulatzeko zailak ziren sistema kuantiko asko klasikoki simulatzeko. Bereziki, dimentsio espazial bateko sistema kuantiko asko eta bi dimentsioko sistema kuantiko jakin batzuk simulatu dira, eta emaitza zehatzak lortu. Algoritmo klasiko hauek deskribapen klasiko argitsuak garatzeari esker lortu dira. Aldi berean, lehen sinpleak ziruditen sistema batzuk harrigarriro konplexuak direla jakin dugu. Ikerketa horiek argitu dute zein sistema kuantiko diren simulatzeko errazak eta zein zailak.
Laugarren aurrerapena komunikazio-kanal kuantikoen ulermenean sakontzea izan da. Teoria eder eta oso bat garatu da egoera kuantiko korapilatsuak kanal kuantikoen gaineko komunikazio klasikoan nola lagundu dezaketen jakiteko. Komunikaziorako protokolo kuantiko asko familiatan antolatu dira, eta, hala, informazio kuantikoarekin posiblea den komunikazio-mota ezberdinen ulermenaren zati handi bat bateratu da.
Konputazio-arazo sakonak ebazteko aukera
Informazio kuantikoaren zientzian lan egiteko motibazio nagusietako bat algoritmo kuantiko azkarrek konputazio-arazo garrantzitsuak ebazteko aukera da. Hemen, azken hamarkadan izandako aurrerapena mistoa izan da: ahalegin handia egin den arren, algoritmo nagusien ideiak duela 10 urte bezala daude. Baina aurrerapen teknikoa nabarmena izan da. Hori bai, oraindik ez dugu ulertzen zer den zehazki ordenagailu kuantikoak indartsu egiten dituena, edo zer arazo-motatan espero daitekeen ordenagailu klasikoak gainditzea.
Datozen urteetan, ordenagailu kuantikoek ez dute bakarrik konputazio-ahalmen handiagoa ekarriko; beharrezkoak ditugu energiaren problema ebazteko. Ordenagailu kuantiko batek hobekuntza parekoa lortuko luke energia aldetik lau qubit gehiagorekin; ia energia-igoerarik gabe, problema zailak ebatziko lituzke. Horregatik ez da beharrezkoa kalkulu-denboraren murrizketa handi bat lortzea konputazio kuantikoak ekar dezakeen energia-aurrezpena hautemateko: abantailak kalkulu kuantikotik harago daude.
* Qubit (edo bit kuantikoa) bit klasiko baten analogo mekaniko kuantikoa da.
Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia