Would we be able to fight a zombie epidemic?
The Walking Dead
Several science fiction stories narrate zombie apocalypse. In these cases, after the death of the man is resurrected and becomes zombie. In most cases, these resurrected beings, the zombies, are human or cannibals. They are clumsy, with the half-lost gaze, with their hands moving forward and clumsy. Despite not being the fastest predators, zombies are able to approach, die and die to humans. Humans killed in the hands of zombies become zombies and so their tribe increases. In this situation human beings are dispersed, isolated collectivities are formed and the world becomes a place feared by zombies.
The Walking Dead is a series developed by Frank Darabonte, based on comics by Robert Kirkman and Tony Moore. After waking up from the coma in an old hospital, police officer Rick Grimes does not find the world he left before being in a coma, but the one destroyed by an epidemic of zombies. In the suburbs of Atlanta, a group of plague survivors struggle to survive, led by Rick. Your dream is to look for a land without zombies. In an increasingly famous situation, and as despair imposes itself, the survival instinct leads to anything. Zombies are the hunting beast of this section and want to catch the man.
A simplified mathematical model of predators and dams
If we want to avoid the definitive extinction of pests and/or minority species in a community, we must look at the increase or decrease in population density. Population cycles are essential tools to understand the variations in population density and to predict changes that will occur over a period of time, in which the population of a species grows and decreases in a recurrent manner. Thus, predator and dam models have been an important part of these research and express the effort to model ecology through mathematical models. Alfred Lotka and Vito Volterra were in charge of proposing a simplified mathematical model of raptors and prey.
Suppose a predator, for example foxes, eats only rabbits and that in the instant t there is population of foxes a(t) and population of rabbits u(t). In the absence of rabbits, foxes would die according to the differential equation a'(t) = -> .a(t), being the constant -{ the parameter of difference between the birth rate and the mortality of foxes. In the absence of steels, the rabbit population would grow exponentially following the differential equation u'(t)=<unk> .u(t), being the parameter of difference between the birth rate and the mortality of rabbits.
If you want to model the situation in which the amounts of both populations are positive, in the differential equation of foxes you will have to add a summing that will be positive when there are rabbits and the more rabbits there are more. In addition, this addition must be high when the number of rabbits and foxes are high. Also, in the differential equation of rabbits should be added another addition. In this case, the addition we will add will be negative in a situation where there are foxes: when there are foxes, the foxes will eat rabbits and therefore the number of rabbits will decrease. In addition, the higher the number of foxes, the greater the decrease in the number of rabbits, so this adding negative should be proportional to the number of foxes. Considering this, and considering that the initial figures of rabbits and foxes are u(0) and a(0), the predator and prey model is called the Lotka-Volterra model and is given by:
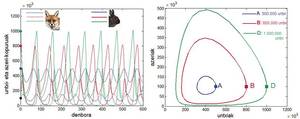
u'(t) = u(t)(<unk> -?a(t)
a'(t) = -a(t)(}
It is a model with meaning, since as the number of foxes increases the rhythm that changes the number of rabbits, ie u'(t), decreases and when the number of rabbits increases the speed of reproduction of rabbits. It is a system of differential equations with cyclical result: if rabbits are added, the number of foxes will increase due to increased food and when the number of foxes will increase. The decrease of the rabbits will mean a decrease of the foxes, which will cause an increase of the rabbits that we will be back at the initial point completing the cycle.
The balance in this model occurs when neither of the two populations are altered, that is, when both derivatives are worth zero. This occurs when the number of rabbits and the number of foxes are null, u(t) = a(t) = 0, or a (t) = <unk>/b and u(t) ={/?. In the first solution, both species disappear; in the second, the number of both populations remains fixed over time.
But are these cycles common in nature? Is this model capable of adequately predicting population changes? The answer is negative, as the unique capture and unique capture model presented is too simplified. In reality there is a context in which there is more than one predator and one prey, and it becomes very complex. However, although the Lotka-Volterra model has not adequately modeled what is happening in the real world, it has given way to more complex models of predators and dams that have contributed to a better understanding of the ecological community and to the regularization of predator and prey cycles.
Some mathematical models of a zombie epidemic
Basic model
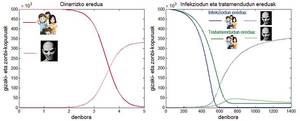
One of the examples used in modeling population densities using mathematical models is that of zombies. When the predator and prey model consists of zombies and humans, three groups can be considered: that of humans (G), that of zombies (Z) and that of dead humans and zombies (H). In this model the number of humans is supposed to increase by the birth rate (which we will call©) and decrease by two reasons: by natural causes and by the influence of zombies. The number of zombies decreases by human action, that is, because humans can kill them. Humans and dead zombies, both for natural causes and in the hands of zombies, will form group H. The beings of this group can resurrect and become zombies. Thus, the possibilities of expanding the set of zombies are two: transform humans into zombies in interaction with the zombies and convert those of the group of dead into zombies.
The formulation of this model is done by three differential equations, and the sum of the changes in the three groups provides the birth rate of human beings G'+Z'+H' =©. This means that over time the sum of the amounts of the three groups will be infinite. Or what is the same, when t??ltima, G+Z+Hâ> will be <br class="xliff-newline" /> 0). As the number of human beings does not tend to infinity, infinity will be the sum of the other two groups, meaning that the zombie epidemic will end civilization.
Model with infection
The model we just described is very basic and it is possible to build more realistic models than it. For example, in one of those models it can be considered that when the zombies contaminate the man, the man does not immediately become zombie, but, after a period of time as contaminated, the man can die or become zombie. As in the basic model, if the human birth rate is not zero, in this model the zombie epidemic will cause the disappearance of humans, although in this case it will take longer than in the previous one.
Model with treatment
In the two models observed so far (basic and infectious), more or less quickly the world is left without human beings and zombies appropriate the world. But is it possible to think of a model in which both species coexist?
In the arena where there is a group of infected or infected we will add a healing treatment for humans. This treatment can take zombies to human status. This does not mean that once converted into human beings they cannot be zombies again. That is, treatment does not involve immunity. If we analyze the situation in which the treatment is located, we will observe that the treatment can not cause the disappearance of the number of zombies. Zombies will exist, but man will not disappear from the world. That is, in a model in which there is treatment the two species will coexist in the world.
Does the world depend on zombies or humans?
Who will prevail in a science fiction context? Will zombies predominate, as indicated by the mathematical model, or, as we are in fiction, will humans face zombies? Here, at least, we have given some idea to the scriptwriters of The Walking Dead for the series to continue.
But is it possible to end the plague of zombies? And if there is, will serial scriptwriters think of any of those models that will eliminate zombies forever?
There are models in which man prevails over zombies. Who can think of such a model? Those of the series The Walking Dead seem to know some example of them, which can result in that the human being has not completely disappeared in the three seasons that the series carries.







