Seríem capaços de combatre una epidèmia de zombis?
The Walking Dead
Diverses històries de ciència-ficció narren apocalipsi de zombis. En aquests casos, després de la mort de l'home es ressuscita i es converteix en zombi. En la majoria dels casos, aquests éssers ressuscitats, els zombis, són humans o caníbals. Són maldestres, amb la mirada medio perduda, amb les mans cap endavant caminant i es mouen maldestres. Malgrat no ser els depredadors més ràpids, els zombis són capaços d'acostar-se, morir i morir als humans. Els humans morts en mans dels zombis es converteixen en zombis i així la seva tribu augmenta. En aquesta situació els éssers humans es dispersen, es formen col·lectivitats aïllades i el món es converteix en un lloc temut pels zombis.
The Walking Dead és una sèrie desenvolupada per Frank Darabonte, basada en els còmics de Robert Kirkman i Tony Moore. Després de despertar-se de la coma en un vell hospital, la policia Rick Grimes no troba el món que va deixar abans d'estar en coma, sinó el destruït per una epidèmia de zombis. En els suburbis d'Atlanta, un grup de supervivents de la pesta lluita per sobreviure, liderat per Rick. El seu somni és buscar una terra sense zombis. En una situació cada vegada més famosa, i mentre la desesperació s'imposa, l'instint de supervivència els porta a qualsevol cosa. Els zombis són la bèstia caçadora d'aquesta secció i volen atrapar a l'home.
Un model matemàtic simplificat de predadors i preses
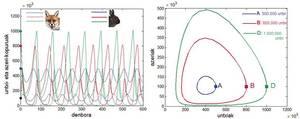
Si es vol evitar l'extinció definitiva de plagues i/o espècies minoritàries en una comunitat, cal fixar-se en l'augment o disminució de la densitat de població. Els cicles de població són instruments imprescindibles per a comprendre les variacions de la densitat de població i preveure els canvis que es produiran en un període de temps, en els quals la població d'una espècie creix i disminueix de manera recurrent. Així, els models de predadors i preses han estat una part important d'aquestes recerques i expressen l'esforç de modelar l'ecologia mitjançant models matemàtics. Alfred Lotka i Vito Volterra van ser els encarregats de proposar un model matemàtic simplificat de rapinyaires i preses.
Suposem que un depredador, per exemple guineus, menja únicament conills i que en l'instant t hi ha població de guineus a(t) i població de conills o(t). En absència de conills, les guineus moririen d'acord amb l'equació diferencial a'(t) = -> .a(t), sent la constant -{ el paràmetre de diferència entre la taxa de natalitat i la mortalitat de les guineus. En absència d'acers, la població de conill creixeria exponencialment seguint l'equació diferencial o'(t)=?.o(t), sent ? el paràmetre de diferència entre la taxa de natalitat i la mortalitat dels conills.
Si es vol modelar la situació en la qual les quantitats de totes dues poblacions són positives, en l'equació diferencial de les guineus caldrà afegir un sumand que serà positiu quan hi hagi conills i quants més conills hi hagi més. A més, aquest sumand haurà de ser alt quan el nombre de conills i de guineus siguin elevats. Així mateix, en l'equació diferencial dels conills haurà d'afegir-se un altre sumand. En aquest cas, el sumand que afegirem serà negatiu en una situació en la qual hi ha guineus: quan hi hagi guineus, les guineus menjaran conills i, per tant, disminuirà el nombre de conills. A més, com més gran sigui el nombre de guineus, major serà la disminució del nombre de conills, per la qual cosa aquest sumand negatiu haurà de ser proporcional al nombre de guineus. Tenint en compte això, i tenint en compte que les xifres inicials de conills i guineus són o(0) i a(0), el model de predadors i preses es denomina model Lotka-Volterra i ve dau per:
o'(t) = o(t)(?-?a(t)
a'(t) = -a(t)(})
Es tracta d'un model amb sentit, ja que a mesura que augmenta el nombre de guineus el ritme que canvia el nombre de conills, és a dir, o'(t), disminueix i quan augmenta el nombre de conills augmenta la velocitat de reproducció dels conills. Es tracta d'un sistema d'equacions diferencials amb resultat cíclic: si s'afegeixen conills, el nombre de guineus augmentarà a causa de l'augment del menjar i quan el nombre de guineus augmenti disminuirà. La disminució dels conills suposarà una disminució de les guineus, la qual cosa provocarà un augment dels conills que tornarem a estar en el punt inicial completant el cicle.
L'equilibri en aquest model es produeix quan no s'alteren cap de les dues poblacions, és a dir, quan totes dues derivades valen zero. Això ocorre quan el nombre de conills i el nombre de guineus són nuls, o(t) = a(t) = 0, o a (t) = ?/b i o(t) ={/?. En la primera solució, totes dues espècies desapareixen; en la segona, el número de totes dues poblacions roman fix en el temps.
Però aquests cicles són habituals en la naturalesa? És capaç aquest model de predir adequadament els canvis de població? La resposta és negativa, ja que el model de captura única i de captura única presentat és massa simplificat. En la realitat es dóna un context en el qual hi ha més d'un depredador i una presa, i es fa molt complex. No obstant això, a pesar que el model Lotka-Volterra no ha modelat adequadament el que ocorre en el món real, ha donat pas a models més complexos de predadors i preses que han contribuït a una millor comprensió de la comunitat ecològica i a la regularització dels cicles de predadors i preses.
Alguns models matemàtics d'una epidèmia de zombis
Model bàsic
Un dels exemples utilitzats en el modelatge de densitats de població mitjançant models matemàtics és el dels zombis. Quan el model de predadors i preses està format per zombis i éssers humans, es poden considerar tres grups: el dels éssers humans (G), el dels zombis (Z) i el dels humans morts i zombis (H). En aquest model se suposa que el nombre d'éssers humans augmenta per l'índex de natalitat (que anomenarem©) i disminueix per dos motius: per causes naturals i per la influència dels zombis. El nombre de zombis disminueix per l'acció humana, és a dir, perquè els éssers humans poden matar-los. Els éssers humans i els zombis morts, tant per causes naturals com en mans de zombis, formaran el grup H. Els éssers d'aquest grup poden ressuscitar i convertir-se en zombis. Així, les possibilitats d'ampliar el conjunt de zombis són dos: transformar als éssers humans en zombis en interacció amb els zombis i convertir als del grup de morts en zombis.
La formulació d'aquest model es realitza mitjançant tres equacions diferencials, i la suma dels canvis en els tres grups proporciona l'índex de naixement dels éssers humans G'+Z'+H' =©. Això significa que amb el pas del temps la suma de les quantitats dels tres grups serà infinita. O cosa que és el mateix, quan t??ltima, G+Z+Hâ> ser?? <br class="xliff-newline" /> 0 ). Com el nombre d'éssers humans no tendeix a l'infinit, infinit serà la suma dels altres dos grups, la qual cosa significa que l'epidèmia dels zombis acabarà amb la civilització.
Model amb infecció
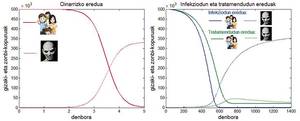
El model que acabem de descriure és molt bàsic i és possible construir models més realistes que ell. Per exemple, en un d'aquests models es pot considerar que quan el zombis contamina a l'home, l'home no es converteix immediatament en zombi, sinó que, després d'un període de temps com contaminat, l'home pot morir o convertir-se en zombi. Igual que en el model bàsic, si la taxa de natalitat humana no és nul·la, en aquest model l'epidèmia de zombis provocarà la desaparició dels éssers humans, encara que en aquest cas es trigarà més temps que en l'anterior.
Model amb tractament
En els dos models observats fins ara (bàsic i infecciós), més o menys ràpid el món queda sense éssers humans i els zombis s'apropien del món. Però, és possible pensar en un model en el qual totes dues espècies convisquin?
En la sorra en la qual existeix un grup d'infectats o infectats afegirem un tractament curatiu per als éssers humans. Aquest tractament pot portar els zombis a estat humà. Això no vol dir que una vegada convertits en éssers humans no puguin tornar a ser zombis. És a dir, el tractament no implica immunitat. Si analitzem la situació en la qual es troba el tractament, observarem que el tractament tampoc pot provocar la desaparició del nombre de zombis. Els zombis existiran, però l'home no desapareixerà del món. És a dir, en un model en el qual hi ha tractament conviuran les dues espècies en el món.
El món depèn dels zombis o dels éssers humans?
A qui prevaldrà en un context de ciència-ficció? Predominaran els zombis, tal com indica el model matemàtic, o, com estem en la ficció, l'ésser humà s'enfrontarà als zombis? Aquí, almenys, hem donat alguna idea als guionistes de The Walking Dead perquè la sèrie continuï.
Però, és possible posar fi a la pesta dels zombis? I, si hi ha, se'ls ocorrerà als guionistes de sèrie algun d'aquests models que eliminarà els zombis per sempre?
Hi ha models en els quals l'home preval sobre els zombis. Qui pot pensar en un model així? Els de la sèrie The Walking Dead semblen conèixer algun exemple d'ells, la qual cosa pot derivar en què l'ésser humà no hagi desaparegut completament en les tres temporades que porta la sèrie.







