Outre-mer oublié ou les gens savent qui est le moment linéaire?
Fisikan doktorea. Bilboko Ingeniaritza Goi Eskolako irakasle eta ikertzailea
EHU
Il y a des grandeurs physiques très connues, comme la vitesse, la force, la puissance, le travail, l'énergie… qui sont très célèbres et qui sont connues non seulement par les scientifiques, mais par tout autre.
Vitesse ? Oui, bien sûr, il indique la rapidité des déplacements, en mètres par seconde, ou en kilomètres par heure, pour mesurer les mouvements des automobiles (et mettre des amendes), etc.
Force ! Qui ne connaît pas la force ? Les harrijasotzailes ont quelque chose de terrible, les rameurs agissent aussi à fond… l'unité de force porte le nom du célèbre Newton, bien que ce soit une combinaison d'unités simples : kg·m/s2.
Puissance ! Honorable… La grandeur sacrée avec laquelle nous valorisons appareils et instruments! Les voitures ont besoin au maximum, les appareils ménagers aussi… L'unité est le watt (kg·m2/s3) et l'unité de puissance équivalente…
Travail ou énergie. C'est aussi très prestigieux. Il est parfois quelque peu déroutant car il existe de nombreux types d'énergie: potentiel, cinétique...; tous les types d'énergie ont la même unité, une autre dénomination digne: juillet (kg·m2/s2).
Quelque chose de plus caché que ces grandeurs si célèbres, il y a une autre grandeur physique, plus inconnue que celles mentionnées; elle n'est pas célèbre… presque personne ne la mentionne. Il est toujours dédié aux travaux cachés. Toujours dans l'obscurité et personne ne s'en rend compte. Cependant, c'est une grandeur physique de grande importance. Plus important que presque tous. Il vaut la peine d'être cité et traité avec gentillesse.
On l'appelait autrefois quantité de mouvement, mais aujourd'hui un autre nom prévalait : moment linéaire ou P. Multiplier la masse et la vitesse des corps: M·V. C'est un vecteur, c'est-à-dire qu'il a une direction, la même direction que la vitesse. L'unité du moment linéaire (kg·m/s) n'a jamais valu la peine, apparemment, le nom d'un physicien reconnu, car il n'a ni nom court ni nom pour le moment.Or, le moment linéaire gouverne les interactions entre les corps. Elle possède des interactions entre les corps. Je dirais Dieu. Même si le corps va, vient, heurte, brosse, explose, colle ou a tout type d'interaction, le moment linéaire reste: P = cte. Il ne change pas de toute façon. Maintient la valeur. Il en est de même si l'on tient compte de l'ensemble isolé de tous les corps qui interviennent (ce qui est dû à la loi d'action et de réaction de Newton, selon laquelle si un corps exerce une force sur l'autre, l'autre exerce une force de même valeur sur le premier, mais dans le sens contraire: TOUJOURS).
Notez que lorsqu'un corps de toute nature attire ou repousse un autre, quoi qu'il arrive entre les deux, ils ne parviennent pas à changer le moment linéaire total. Par exemple :
Supposons que deux patineurs sont ensemble, debout et soudain se poussent les uns les autres (comme l'un pousse l'autre, ou vice versa, ou les deux se poussent mutuellement).
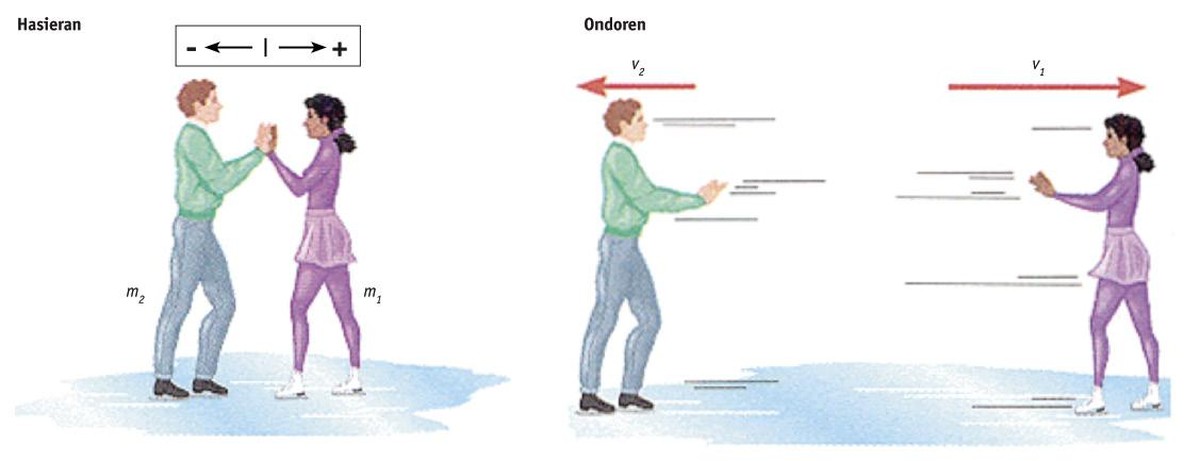
Notons la valeur du moment linéaire, le produit des masses et des vitesses:
Initialement (avant la poussée), Phas= m1·0 + m2·0 = 0 est nul car les deux patineurs sont debout.
Ensuite, ?= m1·v1 + m2·v2
Le moment linéaire ne change pas, donc Phas= ? ou bien: 0 = m1·v1 + m2·v2;
Avec un peu de mathématiques élémentaires, vous pouvez écrire l'expression suivante:
v2/v1 = - m1/m2
Par exemple, si les deux patineurs ont la même masse (m1 = m2) et l'un d'eux, par poussée, prend une vitesse de 1 m/s, l'autre atteindra une vitesse de –1 m/s (égale valeur mais dans le sens inverse). Ou si l'une à 5 m/s, l'autre à 5 m/s. De même, si un patineur a la moitié de la masse (m1/m2 = 0,5), il détecte deux fois la vitesse v1/v2 = 2. Toujours plus rapide (le moins massif). Selon la proportion des masses, les vitesses seront équitablement inversées.
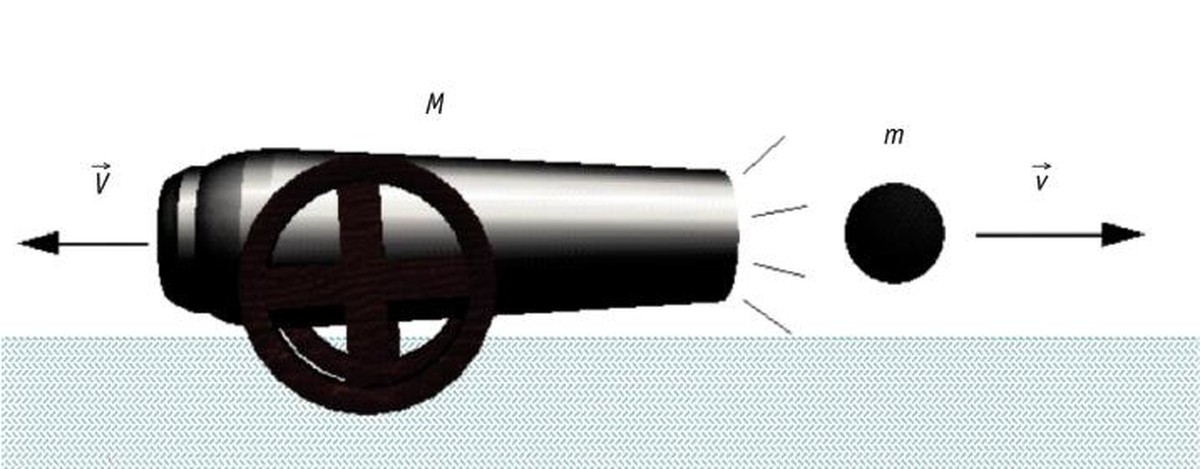
Par exemple, quand un fusil ou un canon se déclenchent, si le rapport de masse est M/m = 100 et que la vitesse de la balle est v = 100 m/s, la vitesse du canon en arrière sera: V = 1 m/s.Cette vitesse de recul du canon est inévitable parce que le moment linéaire établit ainsi la loi d'action et de réaction de Newton ; même quand nous lançons quelque chose, le projectile nous poussera en arrière.
Sur la même ligne, supposons que deux voitures se heurtent et restent collés. Comment savoir où ils se déplaceront après le choc ? En appliquant à nouveau la conservation du moment linéaire:
P avant = m1·v1 + m2·v2 Après = m1·V + m2·V;
S'ils restent adhérents, ils auront la même vitesse (V).
Ecrire après Pllehen = P, d'où vous pouvez calculer la vitesse V après le choc:
m1 v1 + m2·v2 = (m1 + m2)·V; V = (m1v1 + m2·v2) / (m1 + m2)
Il peut même y avoir des arrêts dans certaines conditions : la même masse et des vitesses de même valeur (en sens inverse), la double masse et la moitié de la vitesse, etc., pouvant être combinées avec des conditions préalables à l'impact.

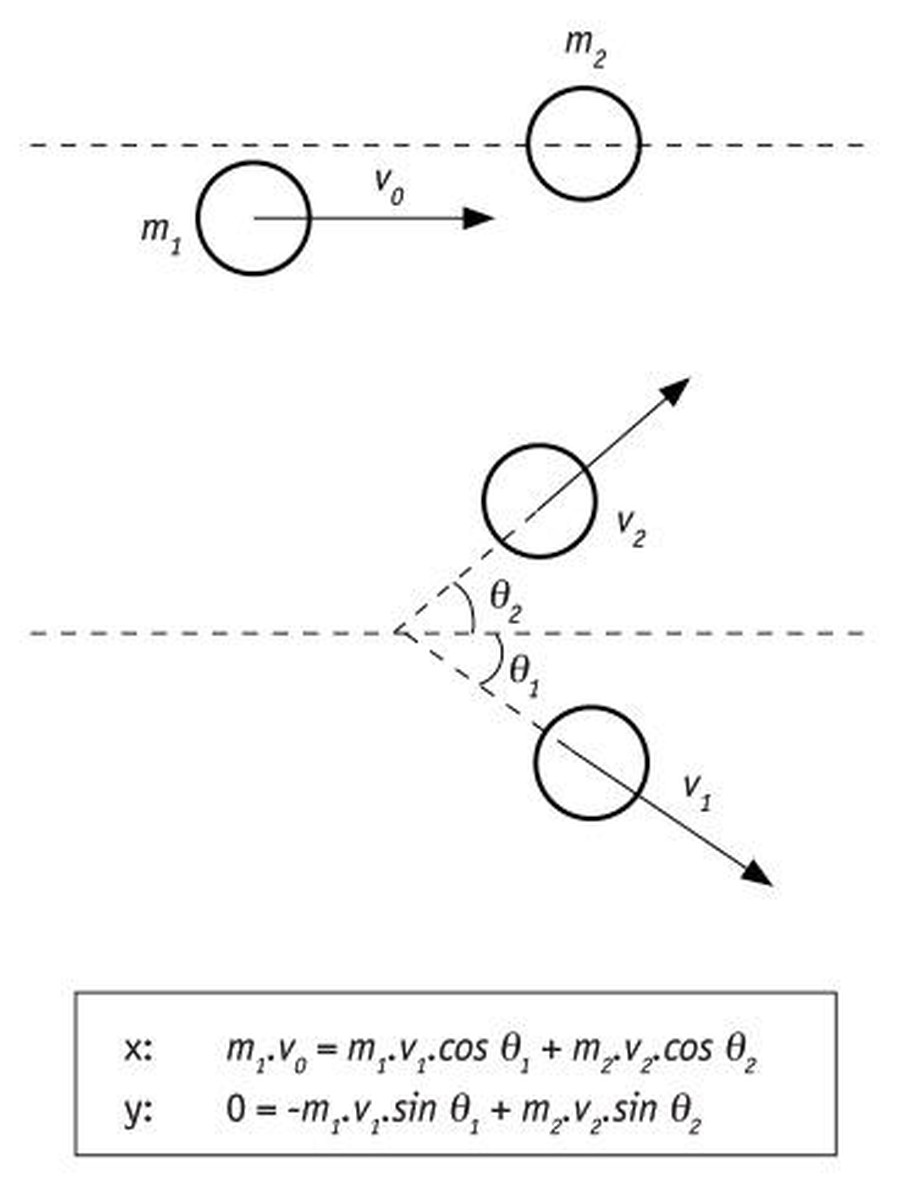
De plus, comme le moment linéaire a un caractère vectoriel, il gouverne aussi les chocs entre boules de billard [1].

Ce caractère vectoriel est analysé dans deux directions conventionnellement (x et y) et en étudiant séparément les deux projections du moment linéaire. Être P constant signifie que les deux projections doivent être constantes à la fois:
Px= cte. et Py = cte.
Dans le cas des patineurs, des canons, des voitures ou des boules de billard, seulement deux corps ont participé à l'interaction, mais il peut y avoir plus de corps, et puis le moment linéaire total est conservé, comme les feux d'artifice. Au moment de l'explosion, si l'explosif est arrêté, la somme des moments linéaires de toutes les parties (explosions symétriques) doit être égale à zéro.

Au contraire, si l'artefact était en mouvement au moment de l'explosion, après l'explosion le moment linéaire doit être le même entre tous les compartiments, et ne sort pas l'explosion symétrique, mais la direction qu'il portait avant.
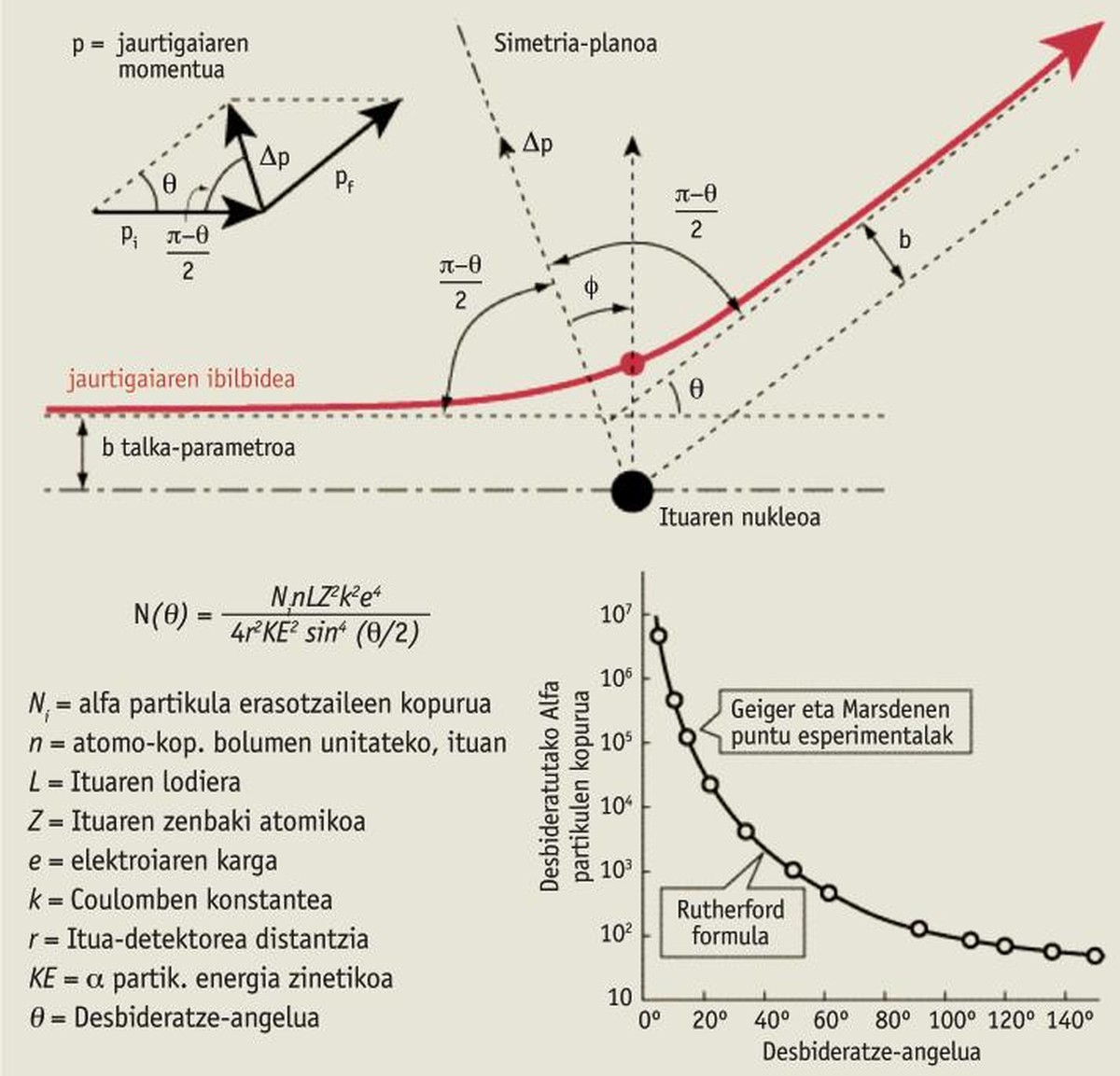
La capacité du moment linéaire couvre tous les domaines de la physique, du niveau microscopique au niveau astronomique. Des chocs ou des explosions entre astéroïdes et planètes aux interatomes. Par exemple, dans la tentative de comprendre et d'expliquer la structure des atomes, Ernest Rutherford a découvert le noyau des atomes en 1911 grâce à la «conservation du moment linéaire».
Ainsi, Rutherford a découvert les rayons alpha dans le rayonnement émis par les éléments radioactifs (charge électrique positive et énergie très élevée), découvrant par la suite qu'ils sont des noyaux d'hélium, unis à deux protons et deux neutrons, et, pour mieux connaître ces particules alpha, il a eu l'idée de lancer une gamme de rayons alpha contre un fin papier d'or. Il l’a promis à deux jeunes étudiants: Hans Geiger et Ernest Marsden. Ils espéraient que ce puissant rayon traverserait de côté à côté ce fin papier d'or, même s'il s'en dévierait un peu. Le résultat a été surprenant. Presque toutes les particules alpha ont eu un bon parcours, comme prévu, mais certaines d'entre elles se sont grandement détournées et d'autres ont même rebondi en arrière ! Surprenant ! “Lance un coup de canon contre une fine couche de papier et rebondit balles à canon! [2].
L'explication théorique de Rutherford et l'exemple des billes de billard sont très similaires, en appliquant la conservation du moment linéaire, et est parfaitement cohérente avec les résultats de cette expérience (voir tableau ci-joint).
Les conclusions de cette recherche ont révolutionné la structure de l'atome: les atomes doivent avoir un petit centre, le noyau (environ 10-14 m). Ce noyau doit avoir une charge électrique positive et presque toute la masse de l'atome, et autour de lui, laissant presque tout l'espace vide, les électrons doivent être [3]. Si je n'avais pas appliqué la conservation du moment linéaire, je n'aurais pas pu obtenir un tel effet.
En plus de cette importante découverte du noyau de l'atome, la conservation du moment linéaire a apporté de nombreuses autres découvertes.
Rutherford lui-même a postulé le neutron en 1920 en recueillant les masses et les vitesses des produits qui se produisent dans les désintégrations radioactives, mais il n'a pas trouvé de neutron, car n'ayant pas de charge électrique, il est difficile de trouver l'empreinte de neutrons. Douze ans plus tard, en 1932, J. Le physicien anglais Chadwick a découvert expérimentalement ces neutrons. Toujours dans les calculs de désintégration on tient compte du moment linéaire, comme dans le cas des patineurs [4].
En 1923, A. L'Américain Compton a montré qu'en plus des particules de matière, le rayonnement électromagnétique a également un moment linéaire et a servi à renforcer le modèle corpusculaire des photons créés ces dernières années. La démonstration théorique de l'effet Compton utilise aussi la conservation du moment linéaire, comme les boules de billard [5].
Wolfgang Pauli a également utilisé la conservation du moment linéaire en 1930 pour postuler la particule dite neutrino. Et en 1956, C. Cowan et F. Il a été découvert par Reines [6].
Au début de cet article, j'ai mentionné la liste des grandeurs physiques les plus prestigieuses (vitesse, force, puissance…). Je ne voudrais pas prendre de l'importance, mais je pense qu'en haut de cette célèbre liste, il faudrait inclure une autre grandeur: le moment linéaire. Cette ampleur n'est pas suffisamment connue (ultraprécision oubliée) et, comme nous l'avons vu plus loin, devrait prendre place parmi les grandeurs physiques les plus prestigieuses.