Ultraheroi ahaztua edo jendeak ba ote daki nor den momentu lineala?
Fisikan doktorea. Bilboko Ingeniaritza Goi Eskolako irakasle eta ikertzailea
EHU
Badira magnitude fisiko batzuk, oso ezagunak: abiadura, indarra, potentzia, lana, energia… oso ospetsuak dira, eta, zientzialariek ez ezik, beste edonork ere ezagutzen ditu.
Abiadura? Bai, noski; desplazamenduen bizkortasuna adierazten du, metro zati segundotan, edo orduko kilometrotan, automobilen mugimenduak neurtzeko (eta isunak jartzeko), eta abar…
Indarra! Nork ez du ezagutzen indarra? Harri-jasotzaileek izugarria daukate, arraunlariek ere jo eta ke jarduten dute… indar-unitateak Newton ospetsuaren deitura dauka, nahiz eta unitate sinple batzuen konbinazioa den: kg·m/s2.
Potentzia! Ohoretsua… Tresna eta aparatuak balioesteko erabiltzen dugun magnitude sakratua! Automobilek ahalik eta handiena behar dute, etxeko aparatuek ere bai… Watta da unitatea (kg·m2/s3) eta zaldi-potentzia unitate baliokidea…
Lana edo energia. Hori ere nahiko entzutetsua da. Pixka bat nahasgarria suertatzen da batzuetan, energia-mota asko dagoelako: potentziala, zinetikoa...; energia-mota guztiek unitate bera dute, beste deitura ohoragarri bat: joulea (kg·m2/s2).
Magnitude ospetsu horiek baino pixka bat ezkutuago, bada beste magnitude fisiko bat, aipatutako horiek baino ezezagunagoa; ez da ospetsua... ia inork ez du aipatzen. Beti ezkutuko lanetan aritzen omen da. Beti ilunpean, eta inor ez da hartaz jabetzen. Dena den, oso garrantzi handiko magnitude fisikoa da. Ia beste guztiak baino garrantzitsuagoa. Merezi du norbaitek aipatzea eta adeitasunez tratatzea.
Garai batean, higidura-kantitate deitzen zitzaion, baina, gaur egun, beste izen bat gailendu da: momentu lineala edo P. Gorputzen masa eta abiadura biderkatzen ditu: M·V. Bektorea da, alegia, norabidea ere badu, abiaduraren norabide bera. Momentu linealaren unitateak (kg·m/s) ere ez du inoiz merezi izan, nonbait, fisikari ospetsuren baten deiturarik, ez baitu ez izen laburrik ez ezizenik, oraingoz behintzat.Bada, hala ere, momentu linealak gorputzen arteko elkarrekintzak gobernatzen ditu. Gorputzen arteko elkarrekintzetako jaun eta jabe da. Jainkoa esango nuke nik. Nahiz eta gorputza joan, etorri, talka egin, zatitu, lehertu, itsatsi, edo nolanahiko elkarrekintza izan, momentu linealak iraun egiten du: P = kte. Ez da nolanahi aldatzen. Eutsi egiten dio balioari. Berdin balio du, baldin eta parte hartzen duten gorputz guztien multzo isolatu osoa kontuan hartzen badugu (horren zergatia Newtonen akzio-erreakzioaren legean datza; horren arabera, gorputz batek beste bati indarra eragiten badio, besteak ere balio bereko indarra eragiten dio lehenari, baina aurkako noranzkoan: BETI).
Kontuan izan ezazu ezen, edonolako gorputz batek beste gorputz bat erakartzen edo aldaratzen duenean (bien artean gertatzen dena gertatzen dela ere), ez dutela lortzen momentu lineal totala aldatzea. Adibidez:
Demagun patinatzaile bi elkarren ondoan daudela, geldi, eta, halako batean, bultza egiten diotela elkarri (berdin dio batak bestea bultzatzen duen, edo alderantziz, edo biek elkarri bultza egiten dioten).
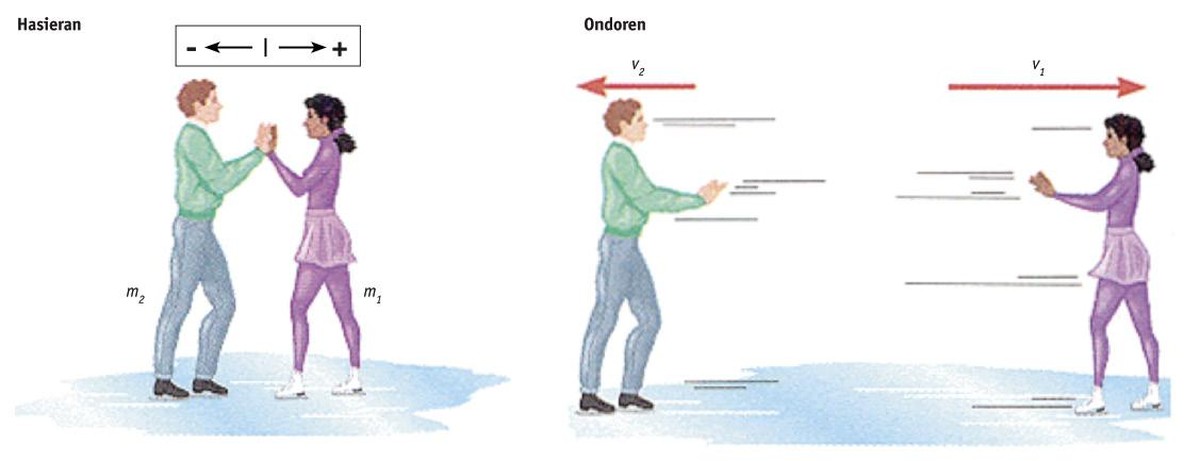
Idatz dezagun momentu linealaren balioa, masen eta abiaduren biderkadura:
Hasieran (bultzada baino lehen), Phas= m1·0 + m2·0 = 0 nulua da, bi patinatzaileak geldi daudelako.
Ondoren, Pond= m1·v1 + m2·v2
Momentu lineala ez da aldatzen; beraz, Phas= Pond edota: 0 = m1·v1 + m2·v2;
Matematika elemental pixka batekin, honako adierazpen hau idatz daiteke:
v2/v1 = - m1/m2
Adibidez, bi patinatzaileek masa bera badute (m1 = m2) eta bietako batek, bultzadaren ondorioz, 1 m/s-ko abiadura hartzen badu, besteak −1 m/s-ko abiadura (balio bera baina aurkako noranzkoan) lortuko du. Edo batak 5 m/s-ko abiadura hartzen badu, besteak −5 m/s-ko abiadura. Halaber, patinatzaile batek masaren erdia badu (m1/m2 = 0,5), bi aldiz abiadura handiagoa atzemango du: v1/v2 = 2. Beti arinena (masa gutxien duena) bizkorrago. Masen proportzioaren arabera, justu alderantzizko proportzioa izango dute abiadurek.
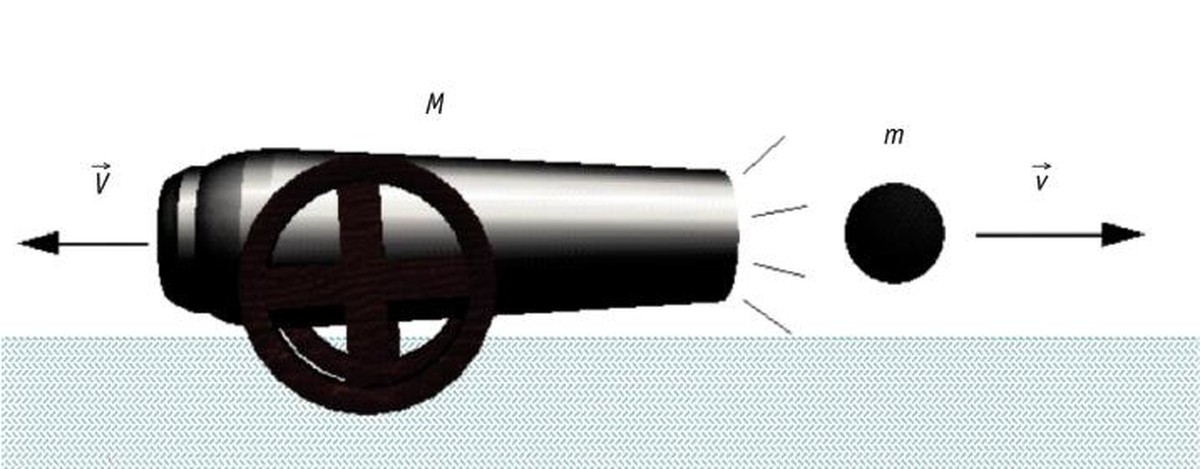
Esaterako, eskopeta batek edo kanoi batek tiro egiten duenean, masen erlazioa M/m = 100 bada eta jakina bada balaren abiadura v = 100 m/s dela, kanoiak abiadura hau izango du atzeraka: V = 1 m/s.Kanoiak atzeraka duen abiadura hori saihestezina da, momentu linealak hala ezartzen duelako, alegia, Newtonen akzio-erreakzioaren legeak; guk zerbait jaurtitzen dugunean ere, atzeraka bultzatuko gaitu jaurtigaiak.
Ildo beretik, demagun bi autok elkarrekin talka egiten dutela eta itsatsita geratzen direla. Nola jakin norantz mugituko diren talkaren ondoren? Bada, berriz ere, momentu linealaren kontserbazioa aplikatuz:
P lehen = m1·v1 + m2·v2 Pondoren = m1·V + m2·V;
Itsatsita geratzen badira, abiadura bera izango dute biek (V).
Plehen = P ondoren idatzi, eta hortik kalkulatu daiteke talkaren ondorengo V abiadura:
m1 v1 + m2·v2 = (m1 + m2)·V; V = (m1v1 + m2·v2) / (m1 + m2)
Geldi ere gera daitezke baldintza zehatz batzuetan: masa bera eta balio bereko abiadurak (kontrako noranzkokoak), edo masa bikoitza eta abiaduraren erdia…; hainbat konbinazio egin daitezke talkaren aurreko baldintzekin.

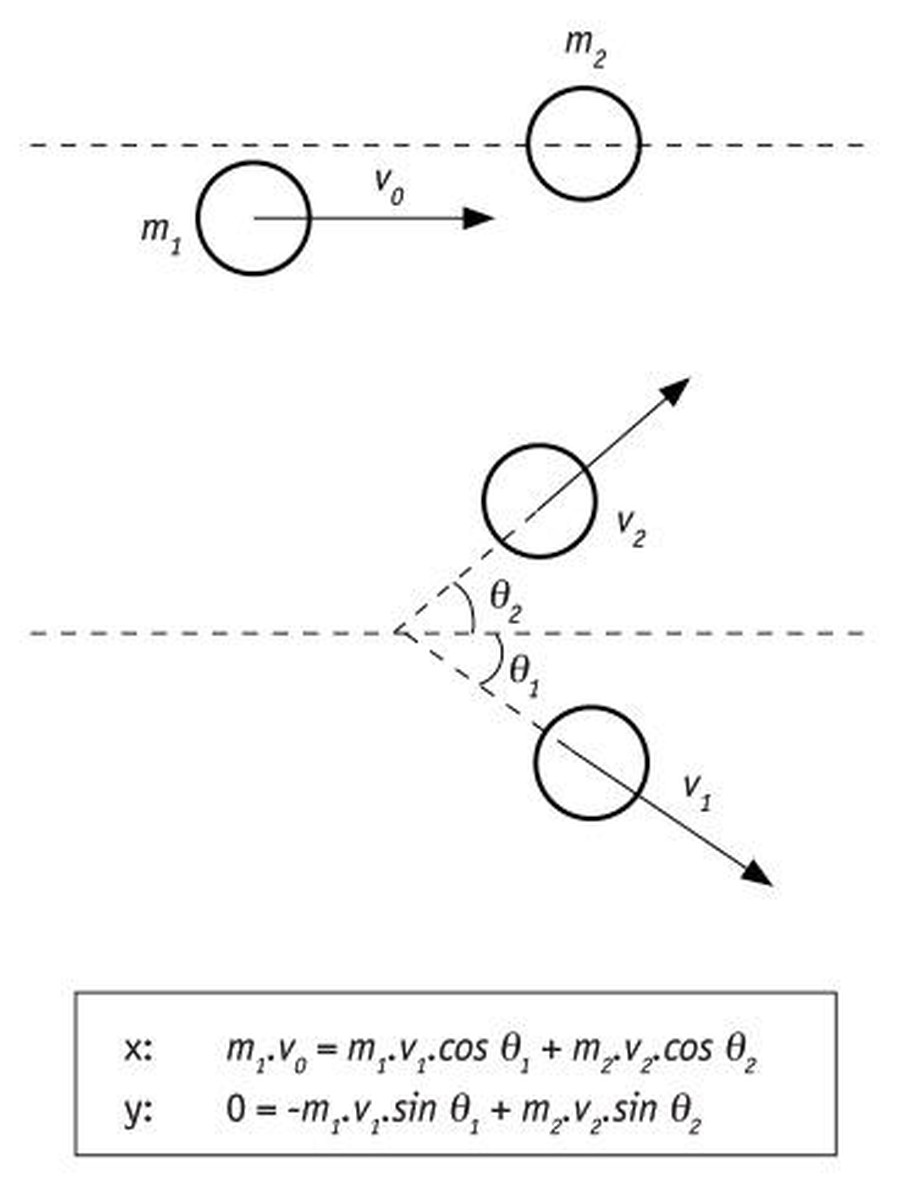
Are gehiago, momentu linealak bektore-izaera duenez, billar-bolen arteko talkak ere gobernatzen ditu [1].

Bektore-izaera hori aztertzeko, bi norabide hartu behar dira konbentzioz (x eta y), eta momentu linealaren bi proiekzioak aztertu, bakoitza bere aldetik. P konstante izateak esan nahi du bi proiekzioek konstanteak izan behar dutela aldi berean:
Px= kte. eta Py = kte.
Patinatzaile, kanoi-bala, auto, zein billar-bolen kasuetan, bi gorputzek soilik hartu dute parte elkarrekintzan, baina gorputz gehiago ere izan daitezke, eta orduan ere momentu lineal totala kontserbatzen da; esate baterako, su artifizialetan. Lehertzen den aldiunean, lehergailua geldi baldin badago, orduan, leherketaren ondoren ere, zati guztien momentu linealen baturak zero eman behar du (leherketa simetrikoak)

Aldiz, lehergailua mugitzen ari bazen leherketaren aldiunean, leherketaren ondoren ere momentu lineal horixe bera izan behar dute zatitxo guztien artean, eta ez da leherketa simetrikoa ateratzen, baizik eta aurretik zeraman norabidearen ingurukoa.
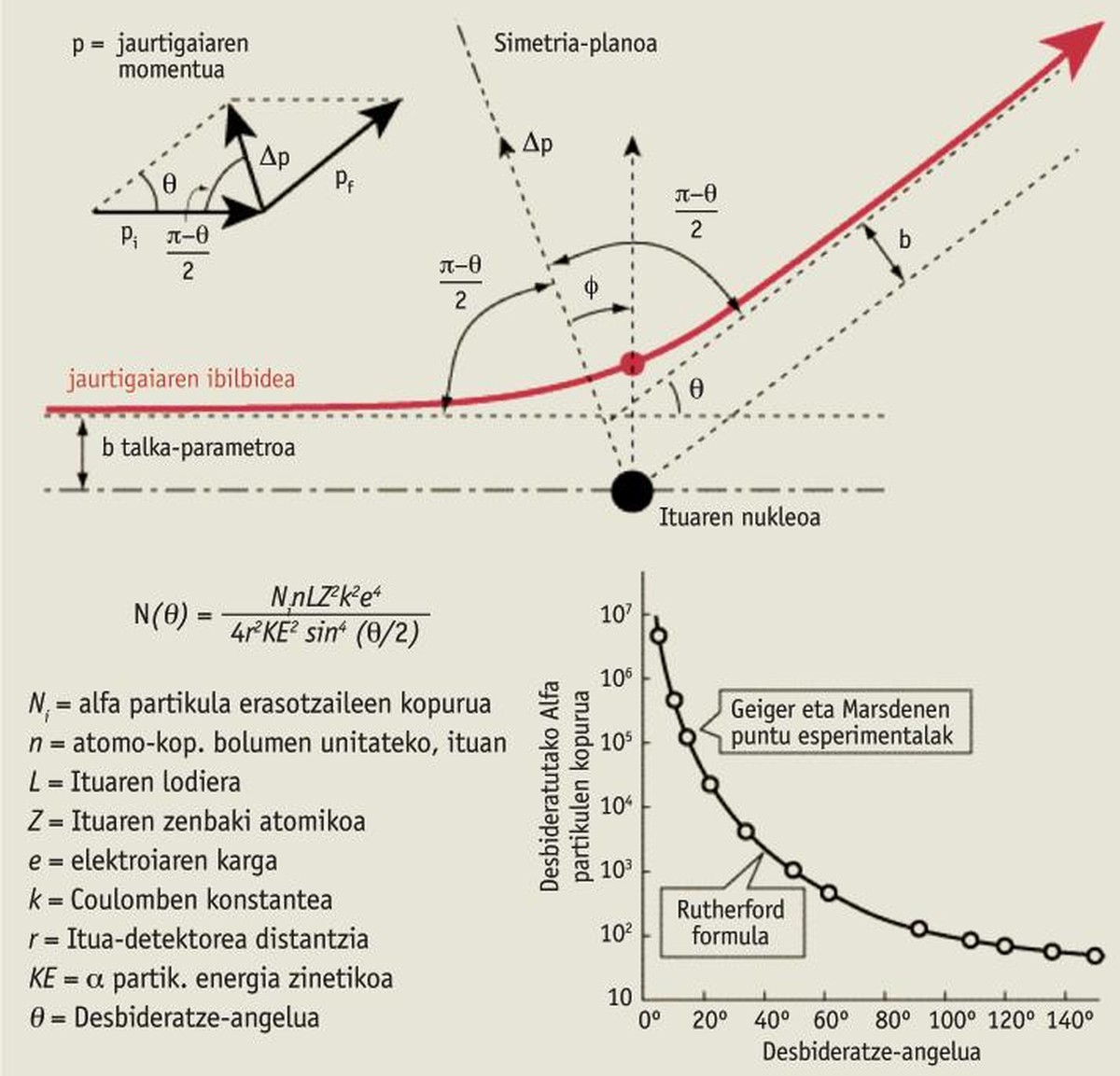
Momentu linealaren ahalmena fisikaren esparru guztietara iristen da, maila mikroskopikotik maila astronomikoraino. Asteroideen eta planeten arteko talka edo leherketetatik, atomoen artekoetaraino. Adibidez, atomoen egitura ulertzeko eta azaltzeko ahaleginean, Ernest Rutherfordek atomoen nukleoa deskubritu zuen 1911. urtean, “momentu linealaren kontserbazioari” esker.
Hala, Rutherfordek alfa izpiak aurkitu zituen elementu erradiaktiboek igorritako erradiazioan (karga elektriko positiboa eta oso energia handia duten izpiak; gerora, helio-nukleoak direla deskubritu zuen, alegia bi protoi eta bi neutroi elkartuta), eta, alfa partikula horiek hobeto ezagutzeko, bururatu zitzaion alfa izpien sorta bat urrezko paper fin baten kontra jaurtitzea. Halaxe agindu zien bere bi ikasle gazteri: Hans Geiger eta Ernest Marsden. Espero zuten izpi indartsu hark urrezko paper fin hura alderik alde zeharkatuko zuela, nahiz eta, agian, pixka bat desbideratuko zen. Emaitza harrigarria izan zen. Ia alfa partikula gehienen ibilbidea zuzena izan zen, espero zen bezala; baina haietako gutxi batzuk izugarri desbideratu ziren, eta beste batzuek baita atzeraka errebotatu ere! Harritzekoa! “Kanoikada bat jaurti paperezko geruza fin baten kontra, eta kanoi-balak errebotatu!!” [2].
Rutherfordek emandako azalpen teorikoa eta billar-bolen adibidea oso antzekoak dira, momentu linealaren kontserbazioa aplikatuz, eta guztiz bat dator esperimentu horren emaitzekin (ikus beheko koadroa).
Ikerketa horren ondorioek iraultza ekarri zuten atomoaren egiturara: atomoek erdigune txiki bat izan behar dute, nukleoa (10−14 m inguru). Nukleo horrek karga elektriko positiboa eta atomoaren ia masa osoa izan behar du, eta, haren inguruan, espazio osoa ia hutsik utzita, elektroiek egon behar dute [3]. Momentu linealaren kontserbazioa aplikatu izan ez balu, ezin izango zukeen horrelako ondoriorik atera.
Atomoaren nukleoaren aurkikuntza garrantzitsu hori ez ezik, beste aurkikuntza asko ere ekarri ditu momentu linealaren kontserbazioak.
Rutherfordek berak, 1920an, neutroia postulatu zuen desintegrazio erradiaktiboetan sortzen diren produktuen masak eta abiadurak bilduz; baina ez zuen neutroia aurkitu, karga elektrikorik ez duenez, zaila baita neutroien arrastoa aurkitzea. Hamabi urte geroago, 1932an, J. Chadwick fisikari ingelesak esperimentalki aurkitu zituen neutroiok. Betiere desintegrazioari dagozkion kalkuluetan, momentu lineala kontuan hartzen da, patinatzaileen adibidean bezalaxe [4].
1923an, A. Compton estatubatuarrak frogatu zuen ezen, materia-partikulek ez ezik, erradiazio elektromagnetikoak ere momentu lineala daukala, eta azken urte haietan sortutako fotoien eredu korpuskularra indartzeko balio izan zuen. Compton-efektuaren frogapen teorikoak ere momentu linealaren kontserbazioa erabiltzen du, billar-bolen antzera [5].
Wolfgang Paulik ere momentu linealaren kontserbazioa erabili zuen, 1930ean, neutrino izeneko partikula postulatzeko. Eta 1956an, C. Cowan-ek eta F. Reines-ek aurkitu zuten [6].
Artikulu honen hasieran, magnitude fisiko ospetsuenen zerrenda aipatu dut (abiadura, indarra, potentzia…). Ez nieke garrantzirik kendu nahi, baina, nire ustez, zerrenda ospetsu horren goiko aldean, beste magnitude bat ere sartu beharko genuke: momentu lineala. Magnitude hori ez da behar bezain ezaguna (ultraheroi ahaztua) eta, geroago ikusi dugunaren arabera, leku bat behar luke magnitude fisiko ospetsuenen artean.
Bibliografia
Idatzi zuk zeuk Gai librean atalean
Gai librean aritzeko, bidali zure artikulua aldizkaria@elhuyar.eus helbidera
Hauek dira Gai librean atalean Idazteko arauak