Exploring the bottoms of dark matter
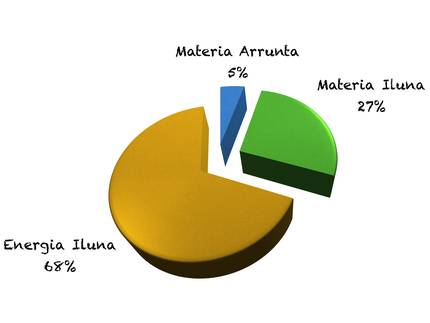
Currently only 5% of the components that make up the universe are known, which is known as common matter. 27% of the mysterious components of the universe are matter and 68% energy, called dark matter and dark energies. Knowing the nature of the dark components, we would be able to explain all the evolution of the universe from birth to the present day. Consequently, what is dark matter? What is it composed of?
The model of the Big Bang Calor1 describes very well the creation and evolution of the universe in which we live. However, this model has suffered throughout history a series of improvements that have allowed us to achieve the success shown today to explain the evolution of the universe. One of the most important improvements occurred when obtaining a thorough observation of several large astronomical objects. In fact, the movement of these objects could not be explained only by common matter. On the road to solving this problem, a hypothetical matter called dark matter was added to the model. At present, dark matter has become an essential element in the standard model of particles, and encompasses most of the non-relativistic matter found in the universe, which moves at speeds much lower than that of light.
One of the most important objectives of the current basic science is to know the basic nature of dark matter (what it is, what its cosmological origin is, what it is composed of, what interactions it has…). And it is that understanding dark matter would be an important step in the search for the basic laws of nature, and finding the particles that form dark matter, in addition, would find a solution to the greatest mystery when describing the evolution of the universe.
In recent years several candidates have been proposed, for the possible presence of dark matter 3,4,5. For example, a heavy particle with a weak interaction (WIMP, of the English weakly interacting massive particle) that, compared to the matter we know today, would be very different and would only have a gravitational interaction; an astrospecific object of heavy compact halo (MACHO, massive ophysical, totally neutral), little or not delicate, of the red light, of the components of the nuc matter.
At present, the experiments that analyze the axions attract enormous attention, since, according to the most advanced theoretical studies, they are the most viable candidates to the dark matter.
However, this does not mean that the axio is fully known and that the problem of dark matter is solved. In the following lines we will try to explain the latest discoveries about axio.
Axion
The Peccei-Quinn6 model was proposed to solve the problem of strong LC. The problem of strong CP appears in quantum chromodynamics (QCD), where strong interaction does not break the symmetry of load parity (CP, from English charge-parity). The axes6 are the inescapable consequence of this model, since the zone of resolution of the problem of the strong CP emits these particles as energy is lost. However, the study of the axions will not only describe the nature of dark matter, but will only solve the problem of strong CP, but the search for these particles and the study of the Cosmic Microwave Fund (CMB) can answer a series of questions about the evolution of the universe. Among other things, the energetic scale of cosmic incorrectness or the problem of the electroweak hierarchy. Therefore, the greatest mystery of the modern standard will help to solve the underarm study.
The mass of the ultra-fast candidates of dark matter that arose during phase transitions in the primitive universe or in the cosmetic Misunderstanding may be between 10-22 eV and 1 keV. A few years ago it seemed impossible to detect particles from these masses. Today, however, it is possible thanks to the new experimental methodologies. On the road to the discovery of the axio, a series of experiments have been proposed using these new methodologies. However, these experiments can only be used to detect an axio with a given mass, since they are based on oscillations of a given frequency and the frequency is determined by the mass of the axio. That is, an experiment should be created for each mass value. As has been commented, the scale of mass that can have the axio is very wide, so it is impossible to take experimentally the whole scale. That is, the hardest thing to experience is to analyze the entire mass scale, so the theoretical determination of the mass of the axio would represent a significant advance in the detection of the axio.
Axial particles can be formed in two forms. One of these assumptions is explained by the mechanism called no alignment 7. In this case, the axions would be produced as a result of non-disturbing effects during the transition of phase QCD. For this mechanism to be important, it would be necessary for the axioiak to be generated through cosmic incorrectness, but from the last investigations it is possible that they have been created after imitation. In this case, topological strings would occur after the spontaneous rupture of the symmetry predicted by the Peccei-Quinn model. These strings, as they lose energy, would emit axions. And once the transition of phase QCD has been produced, the topological strings will disappear.
Topological string networks
The Big Bang heat model we mentioned above explains how the universe has spread from a very dense and warm situation to a more diluted and cold one. That is, the universe expands and cools down. In this cooling the universe has suffered several phase transitions, as well as phase transitions that suffer from water in its cooling process. In these phase transitions, symmetry fractures can be produced, that is, an existing symmetry in the old phase does not appear more in the new phase. Topological differences are a direct consequence of these fractures of symmetry. Depending on the characteristics of the symmetry rupture, the regions that retain the old symmetry may remain in the new phase, and the regions that retain the old symmetry are the topological defections.
The character of the regions that retain the ancient symmetry also depends on the characteristics of the fracture of symmetry: depending on the fracture of symmetry, these regions can have a spherical, string or star shape. When the symmetry proposed by the model Peccei-Quinn is broken, defects appear in the shape of a string, so they are called topological strings. In addition, it must be taken into account that the rupture of symmetry produces several strings forming a three-dimensional network (see figure 2). These rope nets, as they evolve, must emit energy. This energy is emitted in the axions.
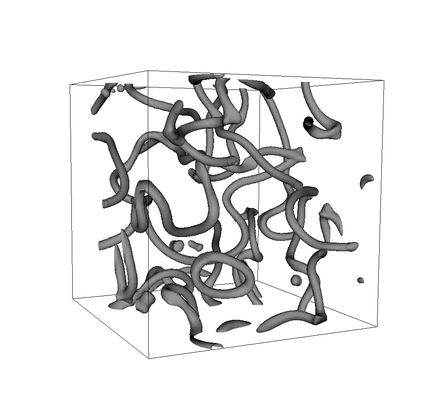
As mentioned above, the theoretical obtaining of the mass of axions is a significant advance in the detection of particles. The theoretical values of mass can be determined by analysis of topologic soka. The only available way to perform this analysis is by numerical simulations.
Numerical simulation
Numerical simulations can reproduce the evolution of the universe and, in addition, evolve in it the topological motifs. In the case of numerical simulations of topological defections, 3-dimensional point networks are used which we will call lattice (see figure 3) to mimic the evolution of the universe. Each latticket point evolves using the motion equations corresponding to the model we want to analyze. That is, the latticket describes the space in three dimensions and through equations of movement is advanced in time. The use of the motion equations described in the model Peccei-Quinn allows to analyze by numerical simulations the cosmic strings that emit axions. With this analysis, the mass of axions emitted by the strings can be determined theoretically.
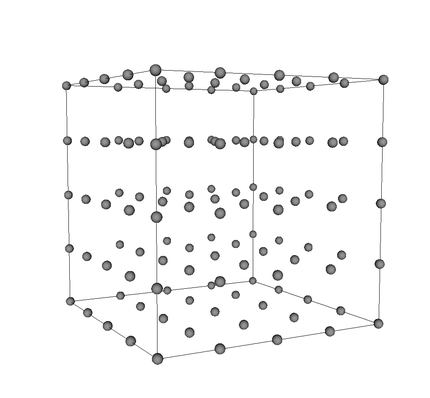
In a recent research8, numerical simulations have been used to analyze the cosmic strings created in the Peccei-Quinn model. In this study, laticés with 4,963 points have been used. To carry out these simulations it has been necessary to work together 1.024 cpus. In this study, the density of topological strings has been analyzed. In fact, knowing the evolution of string density throughout the evolution is very important when it comes to checking the validity of the results. If the density of the strings is constant, the results derived from the simulations can be extrapolated directly to cosmological scales; if not, the results of the simulations are not sufficient to confirm the cosmological effects.
Studies published prior to the aforementioned work assured that the density of the topological strings generated in the Peccei-Quinn model increased over time. This work shows that density is constant. This demonstration is very important when determining theoretically the mass of the axio, since the cosmological validity of the data obtained through numerical simulations has been evident.
This research has shown that numerical simulations will have a great weight when it comes to responding to the question of dark matter. Considering the computational capacity currently available, it will not be surprising that in the near future the exact theoretical value of the mass of axions is. And as has already been commented, this result opens the doors to the discovery of the axio.
References References References References
- S. S. Dodelson, Modern Cosmology. Amsterdam: Amsterdam: Academic Press, 2003.
- G. G. Bertone, D. Hooper, and J. Silk, “Particle dark matter: Evidence, candidates and constraints, Phys. Rept., vol. 405 pp. 279– 390, 2005.
- C. C. Griest. The Search for dark matter: • 1993. [Annals N. And. Acad. Sci. 688,390(1993)].
- M. M. Kamionkowski. WIMP and axion dark matter. In High-energy physics and cosmology. Proceedings, Summer School, Trieste, Italy, June 2-July 4, 1997, pages 394–411, 1997. URL http://alice.cern.ch/format/showfull?sysnb=0260730.
- V. V. Zac. Dark Matter. In Proceedings, 22nd Lake Louise Winter Institute: Fundamental Interactions (LLWI 2007): Lake Louise, Alberta, Canada, February 19-24, 2007, 2007. URL http://inspirehep.net/record/754834/</arXiv:0707.0472.pdf.
- R. R. D. D. Peccei and H. R. R. Quinn, “CP Conservation in the Presence of Instantons,” Phys. Rev. Lett., vol. 38 pp. 1440–1443, 1977.
- M. M. Hindmarsh, J. Lizarraga, A. Lopez-Eiguren, J. Urrestilla, “The scaling density of axion strings”, Phys. Rev. Lett. 124 (2020) no.2, 021301.






