Materia ilunaren barrenak arakatuz

Helsinkiko Unibertsitateko ikertzailea

Zabaldu:
Twitter
Facebook
Emaila

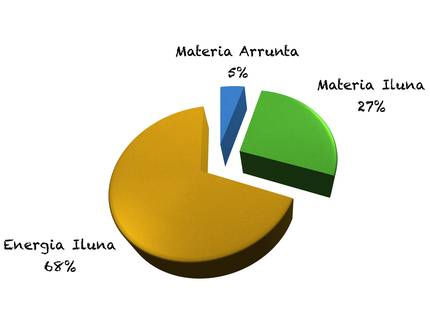
Gaur egun, unibertsoa osatzen duten osagaien % 5 besterik ez da ezagutzen, materia arrunta deritzona. Unibertsoaren osagai misteriotsuen % 27 materia da eta beste % 68, berriz, energia; osagai horiei materia ilun eta energia ilun esaten zaie. Osagai ilunen izaera ezagutuz gero, gai izango ginateke unibertsoaren eboluzio osoa azaltzeko; sorreratik gaur egun arte, alegia. Ondorioz, zer da materia iluna? Zerez dago osatua?

Galaxia baten inguruko materia ilunaren irudikapen artistikoa Arg. Maxwell Hamilton/Flickr

Big Bang Beroaren ereduak¹ oso ondo deskribatzen ditu bizi garen unibertsoaren sorrera eta eboluzioa. Hala eta guztiz ere, eredu horrek hainbat hobekuntza jasan behar izan ditu historian zehar, gaur egun unibertsoaren eboluzioa azaltzeko erakutsitako arrakasta lortu ahal izateko. Hobekuntza garrantzitsuenetariko bat etorri zen hainbat objektu astronomiko handiren behaketa zehatza lortu zenean. Izan ere, objektu horien higidura ezin zitekeen materia arruntarekin soilik azaldu. Arazo hori konpontzeko bidean, materia hipotetiko bat gehitu zitzaion ereduari: materia iluna² izenekoa. Gaur egun, materia iluna ezinbesteko bilakatu da partikulen eredu estandarrean, eta barnean hartzen du unibertsoan aurkitzen den materia ez- erlatibista gehiena —argiaren abiadura baino abiadura askoz txikiagoetan mugitzen den materia—.

Gaur egungo oinarrizko zientziaren helburu garrantzitsuenetariko bat da materia ilunaren oinarrizko izaera ezagutzea (zer den, zer jatorri kosmologiko duen, zerez osatuta dagoen, zer elkarrekintza dituen …). Izan ere, materia iluna ulertzea pauso garrantzitsua litzateke, izadiaren oinarrizko legeak aurkitzeko bidean, eta materia iluna osatzen duten partikulak aurkitzeak, gainera, irtenbidea aurkituko lioke unibertsoaren eboluzioa deskribatzeko orduan dagoen misteriorik handienari.

1. irudia: Unibertsoaren energia-banaketa. Ikus daitekeenez materia arrunta % 5 besterik ez da. Arg. Asier Lopez Eiguren

Azken urteetan, hainbat hautagai proposatu izan dira, materia iluna izan litezkeelakoan^3,4,5. Adibidez: elkarrekintza ahula duen partikula astuna (WIMP, ingelesezko weakly interacting massive particle-tik), zeina gaur egun ezagutzen dugun materiarekin konparatuz oso desberdina litzatekeen eta elkarrekintza grabitazionala besterik ez lukeen izango; halo trinkoko objektu astroﬁsiko astuna (MACHO, ingelesezko massive astrophysical compact halo objects-etik), zeina materia arruntez osatuko litzatekeen, baina oso argi gutxi, edo batere ez, igorriko lukeen, eta neutroi-izarra, nano marroia edo nano zuria izango litzatekeen; axioia, masa oso baxua, kargarik ez eta elkarrekintza ahula edota grabitazionala lituzkeen partikula.

Gaur egun, axioiak aztertzen dituzten esperimentuek izugarrizko arreta erakartzen dute; izan ere, punta-puntako azterketa teorikoen arabera, materia iluna izateko hautagai bideragarrienak dira.

Hala eta guztiz ere horrek ez du esan nahi axioia guztiz ezagutzen denik eta materia ilunaren arazoa konponduta dagoenik. Ondorengo lerroetan, axioiaren inguruko azken aurkikuntzak azaltzen saiatuko gara.

Axioia

Peccei-Quinn⁶ eredua proposatu zen CP sendoaren arazoari irtenbidea aurkitzeko. CP sendoaren arazoa kromodinamika kuantikoan (QCD, ingelesezko sigletan) agertzen da, non elkarrekintza sendoak ez duen karga-paritatearen simetria apurtzen (CP, ingelesezko charge-parity-tik). Eredu horren ezinbesteko ondorio dira axioiak⁶; izan ere, CP sendoaren arazoa konpontzeko erabilitako eremuak partikula horiek igortzen ditu, energia galdu ahala. Hala eta guztiz ere, axioien azterketak ez digu materia ilunaren izaera deskribatuko edota CP sendoaren arazoa konponduko soilik, unibertsoaren eboluzioaren inguruko hainbat galdera erantzun ditzakete partikula horien bilaketak eta Mikrouhinen Hondo Kosmikoaren (CMB, ingelesezko sigletan) azterketak. Besteak beste, inﬂazio kosmikoaren energia-eskala edota hierarkia elektroahularen arazoa. Hortaz, ﬁsika modernoaren misterio handienak erantzuten lagunduko du axioiaren azterketak.

Inﬂazio kosmikoan edota unibertso primitiboan gertaturiko fase-trantsizioetan sortu zen materia ilunaren hautagai ultrarinen masa 10-22 eV eta 1 keV bitartean egon daiteke. Orain dela urte batzuk ezinezkoa zirudien masa horietako partikulak detektatzea. Gaur egun, ordea, metodologia esperimental berriei esker posible da. Axioia aurkitzeko bidean, hainbat esperimentu proposatu dira, metodologia berri horiek erabiliz. Esperimentu horiek, ordea, masa zehatz bat duen axioia detektatzeko bakarrik erabil daitezke; izan ere, maiztasun zehatz baten oszilazioetan oinarritzen dira, eta maiztasuna axioiaren masak zehazten du. Hau da, masa balio bakoitzerako esperimentu bat sortu behar da. Esan bezala, axioiak izan dezakeen masa-eskala oso zabala da, eta, ondorioz, ezinezkoa da esperimentu bidez eskala guztia hartzea. Hau da, esperimentuetan zailena da masa-eskala guztia aztertzea; ondorioz, axioiaren masa teorikoki zehazteak aurrerapauso esanguratsua ekarriko luke axioiaren detekzioan.

Axioi partikulak bi modutara sor daitezke. Balizko egoera horietako bat ez-lerrokatze⁷ izeneko mekanismoaren bidez azaltzen da. Kasu honetan, QCD fase-trantsizioan zeharreko efektu ez-perturbatzaileen ondorioz sortuko lirateke axioiak. Mekanismo horrek garrantzia izan dezan, beharrezkoa litzateke axioiak inﬂazio kosmikoan zehar sortzea, baina azken ikerketetan oinarrituz litekeena da axioiak inﬂazioaren ondoren sortu izana. Kasu horretan, soka topologikoak sortuko lirateke Peccei-Quinn ereduak aurresandako simetria espontaneoki hautsi ondoren. Soka horiek, energia galdu ahala, axioiak igorriko lituzkete. Eta behin QCD fase-trantsizioa gertatuta, soka topologikoak desagertu egingo lirateke.

Soka topologikoen sareak

Lehenago aipatu dugun Big Bang beroaren ereduak azaltzen digu nola zabaldu den unibertsoa oso dentsoa eta beroa zen egoera batetik diluituagoa eta hotzagoa den beste egoera batera. Hau da, unibertsoa zabaltzen eta hozten ari da. Hozte horretan unibertsoak zenbait fase-trantsizio jasan ditu, urak bere hozte-prozesuan jasaten dituen fase-trantsizioen antzera. Fase-trantsizio horietan simetria-hausturak gertatu daitezke, hau da, fase zaharrean zegoen simetria bat ez da gehiago ageri fase berrian. Simetria-haustura horien ondorio zuzena dira defektu topologikoak. Simetria-hausturaren ezaugarrien arabera, simetria zaharra gordetzen duten eskualdeak geratu daitezke fase berrian, eta simetria zaharra gordetzen duten eskualde horiek dira defektu topologikoak.

Simetria-hausturaren ezaugarrien menpe ere badago simetria zaharra gordetzen duten eskualdeen izaera: simetria-hausturaren arabera eskualde hauek esfera-itxura, soka-itxura edota izara-itxura izan dezakete. Peccei-Quinn ereduak proposaturiko simetria hausten denean, soka-itxurako defektuak agertzen dira, eta horregatik deritze soka topologiko. Gainera, kontuan hartu behar da simetria-hausturaren ondorioz hainbat soka sortzen direla hiru dimentsiotako sare bat sortuz (ikusi 2. irudia). Soka sare horiek, eboluzionatu ahala, energia igorri behar dute. Energia hori axioietan igortzen dute.

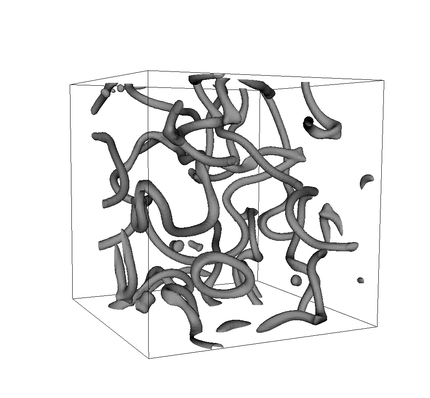
2. irudia: Peccei-Quinn ereduan sorturiko soka topologikoen sarearen irudia. Irudi hau zenbakizko simulazioa erabiliz lortua da. Arg. Asier Lopez Eiguren

Gorago aipatu dugun moduan, axioien masa teorikoki lortzea aurrerapauso nabarmena litzateke partikula detektatzeko orduan. Masaren balio teoriko oso zehatza lor daiteke soka topologikoen sareak aztertuz. Azterketa hori egiteko modu ﬁdagarri bakarra zenbakizko simulazioen bidezkoa da.

Zenbakizko simulazioak

Zenbakizko simulazioek unibertsoaren eboluzioa erreproduzi dezakete, eta, gainera, defektu topologikoek bertan eboluzionatu. Defektu topologikoen zenbakizko simulazioen kasuan, 3 dimentsiotako puntu-sareak erabiltzen dira; lattice deituko diogu sare horri (ikusi 3. irudia), unibertsoaren eboluzioa imitatzeko. Latticearen puntu bakoitza aztertu nahi dugun ereduari dagokion higidura-ekuazioak erabiliz eboluzionatzen da. Hau da, lattice-ak hiru dimentsiotako espazioa deskribatzen du, eta higidura-ekuazioen bidez, denboran aurrera egiten da. Peccei-Quinn ereduak deskribatzen dituen higidura-ekuazioak erabiliz gero, axioiak igortzen dituzten soka kosmikoak azter daitezke, zenbakizko simulazioen bidez. Azterketa honetaz baliatuz, sokek igorritako axioien masa zehatz daiteke teorikoki.

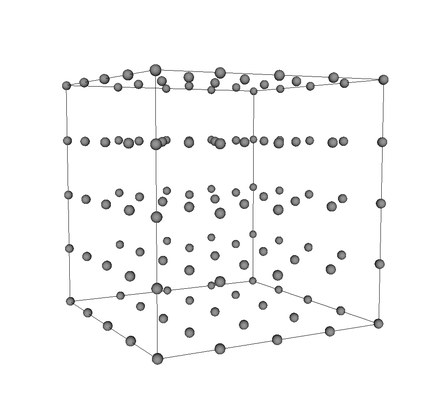
3. irudia: Zenbakizko simulazioetan erabiltzen den lattice-aren irudia. Kasu honek 53 puntu ditu. Arg. Asier Lopez Eiguren

Orain dela gutxi argitaratutako ikerkuntza batean⁸, zenbakizko simulazioak erabili dituzte Peccei-Quinn ereduan sortzen diren soka kosmikoak aztertzeko. Azterketa honetan, 4.963 puntu dituzten latticeak erabili dituzte. Simulazio horiek burutzeko, beharrezkoa izan da 1.024 cpuk batera lan egitea. Lan horretan, soka topologikoen dentsitatea aztertu dute. Izan ere, eboluzioan zehar soken dentsitatearen bilakaera zein izan den jakitea oso garrantzitsua da emaitzen baliotasuna egiaztatzeko garaian. Soken dentsitatea konstantea bada, simulazioetatik eratorritako emaitzak zuzenean estrapola daitezke eskala kosmologikoetara; hori horrela ez bada, simulazioen emaitzak ez dira nahikoak ondorio kosmologikoak baieztatzeko.

Aipaturiko lan horren aurretik argitaratutako hainbat ikerkuntzek ziurtatzen zuten Peccei-Quinn ereduan sorturiko soka topologikoen dentsitatea hazi egiten zela denboran zehar. Lan horrek, aldiz, dentsitatea konstante dela frogatzen du. Frogapen hori oso garrantzitsua da axioiaren masa teorikoki zehazteko orduan, argi geratu baita zenbakizko simulazioen bidez lorturiko datuen baliotasun kosmologikoa.

Ikerkuntza horrek argi utzi du zenbakizko simulazioek pisu handia izango dutela materia ilunaren galderari erantzuna emateko orduan. Gaur egun eskuragarri dagoen ahalmen konputazionala kontuan izanik, ez da harritzekoa izango etorkizun hurbil batean axioien masaren balio teoriko zehatza izatea. Eta lehenago esan bezala, emaitza horrek ateak zabalduko dizkio axioiaren aurkikuntzari.

Erreferentziak

S. Dodelson, Modern Cosmology. Amsterdam: Academic Press, 2003.
G. Bertone, D. Hooper, and J. Silk, “Particle dark matter: Evidence, candidates and constraints,” Phys. Rept., vol. 405, pp. 279– 390, 2005.
K. Griest. The Search for dark matter: WIMPs and MACHOs. 1993. [Annals N. Y. Acad. Sci. 688,390(1993)].
M. Kamionkowski. WIMP and axion dark matter. In High-energy physics and cosmology. Proceedings, Summer School, Trieste, Italy, June 2-July 4, 1997, pages 394–411, 1997. URL http://alice.cern.ch/format/showfull?sysnb=0260730.
V. Zacek. Dark Matter. In Proceedings, 22nd Lake Louise Winter Institute: Fundamental Interactions (LLWI 2007): Lake Louise, Alberta, Canada, February 19-24, 2007, 2007. URLhttp://inspirehep.net/record/754834/ﬁles/arXiv:0707.0472.pdf.
R. D. Peccei and H. R. Quinn, “CP Conservation in the Presence of Instantons,” Phys. Rev. Lett., vol. 38, pp. 1440–1443, 1977.
M. Hindmarsh, J. Lizarraga, A. Lopez-Eiguren, J. Urrestilla, “The scaling density of axion strings”, Phys. Rev. Lett., 124 (2020) no.2, 021301.