Cartes virtuelles de langues
La langue est curieuse. Dans l'écriture comme dans la prononciation, les mots porc et poux sont très similaires, tandis que les mots porc et sanglier sont complètement différents. Parmi les animaux, cependant, les porcs sont beaucoup plus près des sangliers que des poux. En définitive, la relation entre les mots d'une langue et leurs significations est arbitraire, et les relations entre les concepts de porc, de poux et de sanglier ne vivent que dans notre esprit.
Cependant, en faisant une recherche sur Google ou en parlant avec Siri, ce que nous avons si intériorisé devient une grande difficulté pour les machines. Et comme quand nous nous perdons sur la montagne ou sur la route, les machines utilisent des cartes pour avancer dans le labyrinthe des langues. Ces cartes sont appelées Embedding et, à travers elles, le traitement du langage a été internalisé sur des terrains qui semblaient impensables. Nous allons faire ce voyage étape par étape.
De cartes de villes à cartes de mots
Avant d'entrer dans le territoire de la langue, nous nous arrêtons momentanément pour nous fixer sur nos cartes communes. Fondamentalement, les cartes que nous connaissons sont des représentations graphiques d'un territoire, par exemple, qui assignent un point à chaque ville dans chaque cas. Logiquement, pour que les cartes aient du sens, ces points ne sont pas dispersés de quelque façon que ce soit, mais l'emplacement de la carte respecte les distances que nous avons dans la réalité. Ainsi, sur une carte, Paris nous apparaîtra plus près de Bruxelles que de Moscou, car en réalité la capitale française est plus proche de la capitale belge que de la capitale russe.
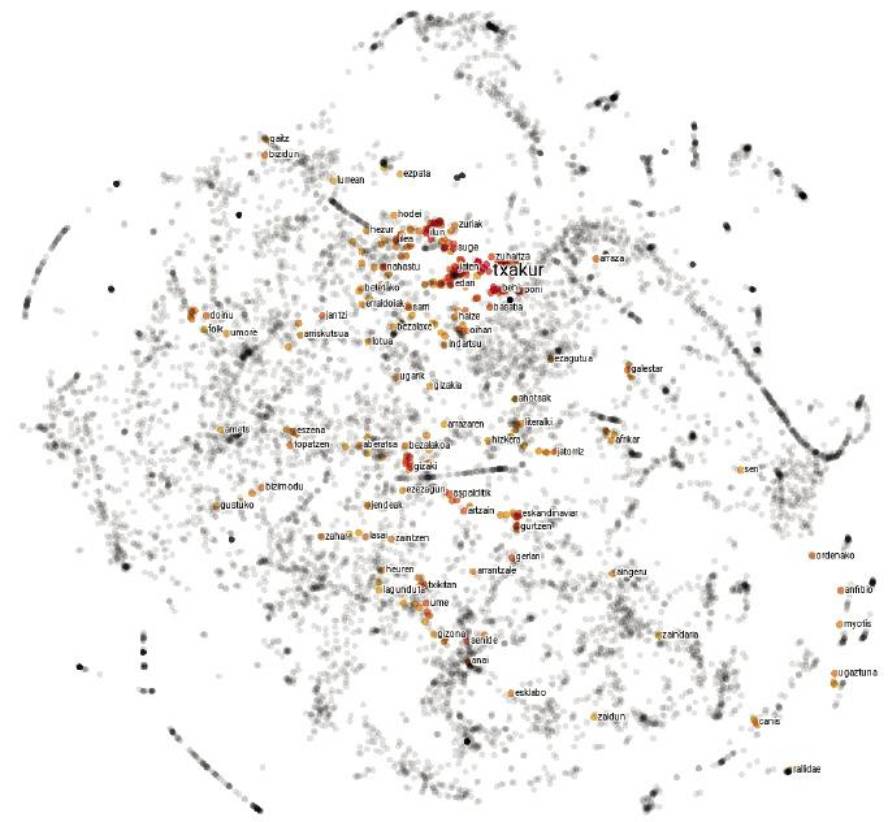
Les cartes de langues ne sont pas très différentes. Au lieu d'expliquer les villes, chaque point représente un mot et les distances entre elles dépendent de la ressemblance sémantique des mots. Par conséquent, sur une carte de ce type, le point correspondant au mot porc sera plus proche de celui correspondant au sanglier que du poux, puisque la similitude sémantique entre les mots porc et sanglier est plus grande que parmi les mots porc et poux.
Mais tout n'est pas si simple : pour saisir correctement la complexité du langage, les 2 dimensions du papier restent courtes, et ces cartes ont généralement environ 300 dimensions. Mais ne vous effrayez pas les grands nombres ! Comme il y a un saut d'une seule dimension de la droite aux deux dimensions du carré, et un saut des deux dimensions du carré aux trois dimensions du cube, vous pouvez imaginer qu'il y a un saut semblable des trois dimensions du cube aux quatre dimensions de la barre, et nous pourrions ainsi continuer jusqu'aux 300 dimensions citées.
Mais comment construire une carte de 300 dimensions si nous vivons en trois dimensions ? Ne vous inquiétez pas, nous n'allons pas commencer! En réalité, ces cartes ne sont pas physiques, mais des objets mathématiques qui vivent dans la mémoire des ordinateurs. En fait, toutes les cartes peuvent être reproduites par des nombres. Pour cela, un système de référence est généralement consensuel, indiquant chaque point en fonction de sa position par rapport aux différents axes. Ainsi, selon la distance angulaire par rapport à l'équateur et au méridien de Greenwich, les coordonnées de Paris (48.86, 2.35) sont celles de Bruxelles (50.85, 4.35) et de Moscou (55.75, 37.62). Ces coordonnées nous permettent, entre autres, de calculer mathématiquement les distances entre les villes. La même chose est faite avec les cartes de langues, mais comme au lieu d'avoir 2 dimensions, 300 nombres sont nécessaires pour décrire chaque point. Car chacune de ces cordes des nombres représentant un mot est ce que nous appelons embedding.
Partant du texte et cartographiant les machines
La réalisation de cartes est un travail laborieux. Les cartographes collectent et analysent diverses photographies, mesures et statistiques, et élaborent des représentations graphiques qui correspondent à ces données. La description des langues a également été faite par l'homme: là sont, entre autres, les dictionnaires qui nous sont si communs. Mais les cartes qui nous occupent ne sont pas manuelles. En analysant de longs textes, les machines les créent automatiquement et c'est une recette simple et efficace.
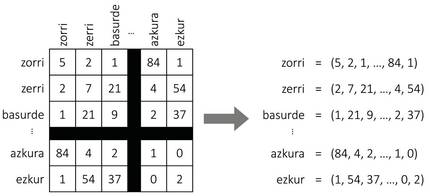
Comme le montre la figure 2, supposons que nous construisions une table géante avec tous les mots d'une langue. Pour chaque mot, nous aurons une ligne et une colonne, de sorte que chaque cellule correspond à une paire de mots. Pour remplir le tableau, nous allons prendre un texte long et compter le nombre de phrases qui apparaissent simultanément chaque couple de mots. Et voilà, nous avons notre carte ! Pour chaque mot nous prendrons la liste des numéros de la ligne correspondante, qui seront les coordonnées du mot.
Même si cela semble un mensonge, cette approche simple génère des cartes assez sensées. En fait, selon l'hypothèse distributive de la sémantique [8, 7], des mots similaires ont généralement des modèles de représentation similaires, de sorte que la procédure précédente leur assignera des coordonnées similaires. Aussi pour notre exemple initial, les mots sanglier ou porc apparaîtront souvent à côté du mot gland et rarement à côté du mot démangeaison, et avec le mot zorri se produira à l'envers. Par conséquent, les porcs et les carreaux auront des coordonnées similaires et resteront proches les uns des autres sur la carte. Les coordonnées des poux seront assez différentes, de sorte qu'il s'éloignera d'eux.
Mais il ya quelque chose qui manque dans cette recette. Et c'est que, bien que les 300 dimensions mentionnées ci-dessus semblaient beaucoup, cette procédure produirait des cartes de dizaines de milliers de dimensions, puisque les langues formeront leurs coordonnées avec autant de mots que de nombres. Comment réduire le nombre de dimensions ? La réponse ne nous est pas très étrange : nos cartes communes ont généralement deux dimensions, bien qu'en réalité on parle d'un monde en trois dimensions. En fait, lors de la création de cartes, la dimension de la hauteur est souvent exclue, car elle n'est pas très significative pour calculer les distances entre les villes. Quelque chose de semblable se fait avec les cartes des langues: en utilisant différentes techniques mathématiques on identifie les axes de plus grande variabilité (les plus significatifs) et on exclut de la carte le reste des dimensions. Malgré quelques adaptations pour corriger l'effet de la fréquence, c'est l'idée de base qui sous-tend les techniques de comptage pour l'étude des embeddings [3]; à noter que les techniques basées sur l'apprentissage automatique [11, 4] suivent la même procédure implicitement [10].
Jouer avec des cartes
Malgré leur simplicité, nos cartes communes cachent plus de secrets qu'il n'y paraît en principe. Bien qu'ils n'aient pas été conçus pour cela, ils servent également à apprécier, par exemple, la température qui se produit partout dans le monde. En fait, les points qui se trouvent aux latitudes extrêmes, les plus proches des pôles, sont généralement plus froids, tandis que les points les plus proches de l'équateur sont plus chauds. De même que l'axe de latitude est lié à la température, dans les cartes des langues on peut aussi identifier des axes similaires qui relient la polarité des mots (degré de positivité et négativité) à d'autres caractéristiques [12]. Grâce à eux, les applications d'analyse automatique des opinions ont acquis une grande force ces derniers temps.
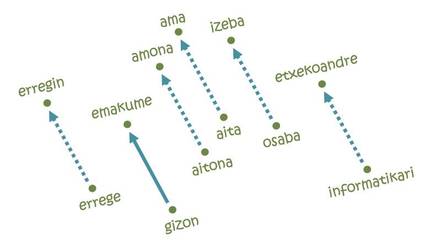
Mais ce qui a rendu les embeddings si populaires a été la résolution d'analogies [11]. L'idée ne peut pas être plus simple: Pour aller de Paris à Bruxelles il faut parcourir 222 km au Nord et 144 km à l'Est; de même, dans chacun des axes de la carte de la langue il faudra une certaine distance du mot homme au mot femme, par exemple. Si nous commençons par le mot roi et suivons les mêmes pas, nous arrivons à la parole erregin ! En fait, la trajectoire étudiée codifie la relation homme-femme et la transfère à son équivalent féminin à partir de n'importe quel mot masculin. De même, on peut réaliser des analogies équivalentes pour les relations pays-capital, singulier-pluriel, présent et passé.
Mais tout n'est pas si beau: si nous commençons par le mot informatique en suivant la même trajectoire d'hommes et de femmes, par exemple, nous arriverions à parler de femmes au foyer [5]. En d'autres termes, selon la carte, l'informatique est une affaire d'hommes, et les tâches ménagères sont des femmes. Que voir, apprendre ceci : les embeddings sont basés sur des textes écrits par des humains et reflètent les mêmes tendances discriminatoires enracinées dans notre société. En fait, selon plusieurs experts, affronter ce type de comportements injustes sera l'un des défis futurs de l'intelligence artificielle.
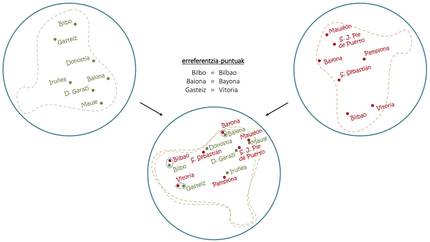
Malgré les problèmes, si avec une seule langue vous pouvez faire ces trucs, combinant des cartes multilingues ont obtenu des choses encore plus étonnantes. Comme on le voit dans la figure 4, comme avec la superposition de cartes en basque et en espagnol on peut extraire les contreprestations en espagnol des capitales basques, avec les embeddings on utilise le même principe de base pour induire des traductions de mots communs [1, 6]. En ce sens, des traducteurs automatiques capables d'apprendre sans aucune conduite humaine [2, 9], de lire des textes longs en plusieurs langues et de réaliser des traductions entre eux sans autres aides ont été développés récemment.
Nouvelles destinations
Bien que notre voyage soit sur le point d'arriver à la fin, le chemin parcouru par les embeddings semble infini. Outre l'amélioration des techniques d'étude et le développement de nouvelles applications, les tentatives d'aborder des phrases ou des textes plus longs à partir de cartes de mots ont pris de la force ces derniers temps. Jusqu'où ce chemin nous mènera, mais il n'apparaît sur aucune carte et, avec de nouveaux objectifs à l'horizon, l'avenir ne pouvait être plus excitant.
Références
Travail présenté aux prix CAF-Elhuyar.