Cando a ficción faise realidade
Ikertzailea eta irakaslea
Euskal Herriko Unibertsitateko Informatika Fakultatea
Cuántica, sempre cuántica
A idea científica que máis se achega ao tipo de teletransporte que vimos en series como Start Trek é a teletransporte cuántico, cuxo obxectivo é transportar un sistema cuántico desde o punto A até o punto B, sen ningún tipo de soporte ou canle física. Pero paira entender todo isto correctamente temos que explicar algunhas das bases da física cuántica. Non te asustes! Porque o faremos dunha maneira moi sinxela.
Caixas e bolitas
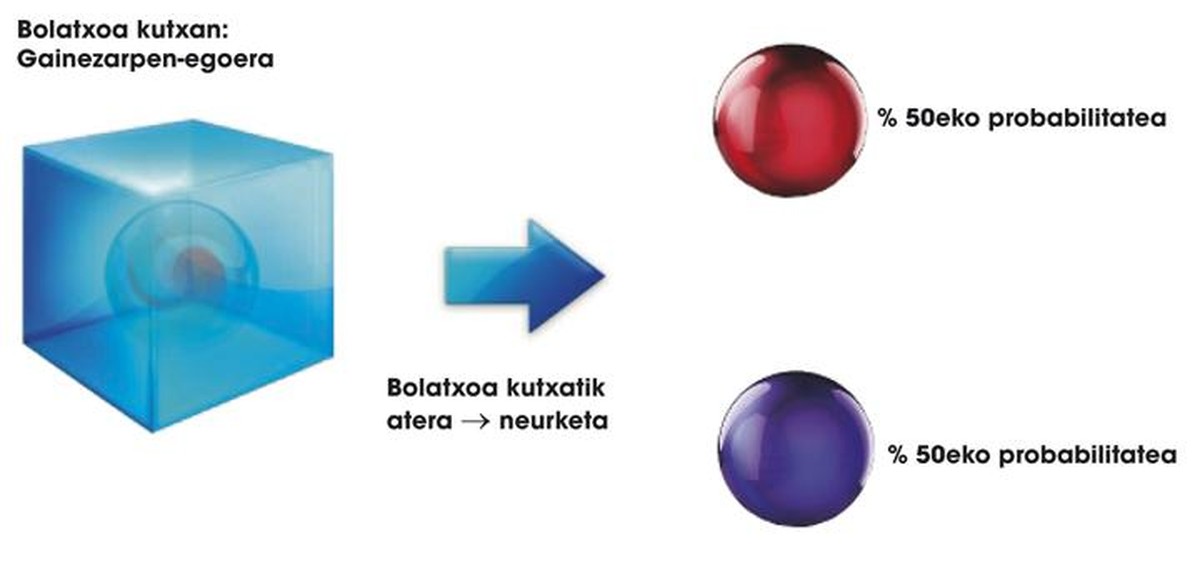
Cando falamos de sistemas cuánticos falamos de conceptos como átomos, electróns, protones ou fotóns. Paira facilitar as cousas, os sistemas cuánticos serán unhas bolitas especiais gardadas nunhas caixas especiais. Estas bolitas poden ter dúas cores: vermello | G> ou azul | Ou>. A primeira peculiaridade destas bolitas é que, mentres permanecen no interior da caixa, poden estar nun estado de combinación de | G> e | Ou> cores:
a | G> + b | U>
onde a e b son dous números reais. O seu significado é sinxelo: indican a probabilidade da cor que terá a bolita ao saír da caixa. É dicir, si una bolita atópase en estado 0,5 | G> + 0,5 | Ou>, ao abrirse a caixa a probabilidade de ter | G> é do 50%. Na cuántica esta propiedade das bolitas chámase propiedade da superposición. Isto lévanos a outra lei especial: as bolitas dentro da caixa poden estar en estado de superposición, pero cando abrimos a caixa só poden ser | G> ou | Ou>. Non hai superposición fóra de caixa. O sinónimo cuántico de apertura de caixa é a medición, onde se anula o estado de solapamiento das bolitas (ver figura 1).
Con todo, as caixas non se utilizan unicamente paira gardar bolitas. Si axita a caixa de forma diferente, podemos cambiar o estado da bolita, por exemplo cambiando as proporcións das combinacións. O equivalente á axitación son operacións cuánticas. Hai moitos tipos e nós non imos profundar. Polo momento, pensa que axitando a caixa somos capaces de realizar as operacións que desexamos.
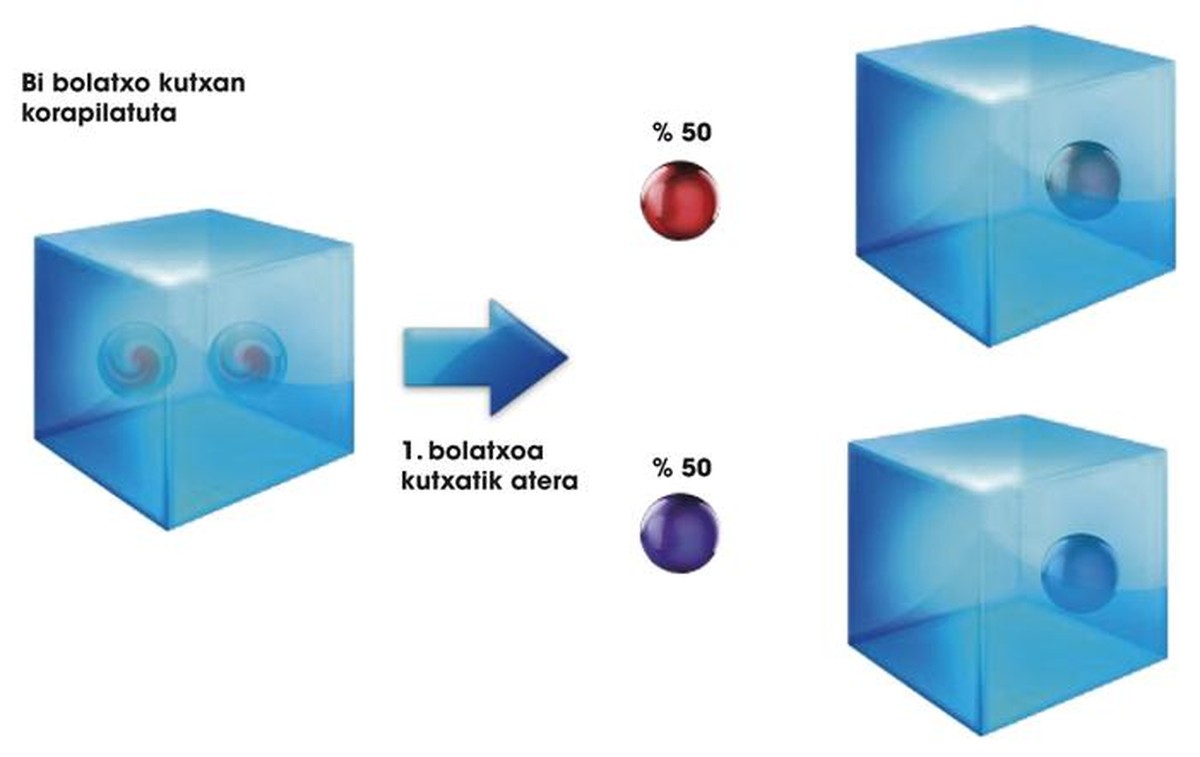
Paira terminar con este apartado, temos que mencionar outra particularidade das nosas caixas e bolitas. Si colocamos dous bolitas na mesma caixa e axitamos a caixa, podemos coroar as bolitas xuntas. Así, axitando a Bolita 1 e a Bolita 2 na mesma caixa, podemos obter o estado 0,5 | G 1 G 2 > + 0,5 | Ou 1 Ou 2 >. En Cuántica, esta situación chámase complicada, xa que as dúas bolitas quedan complicadas. Nesta situación, si da caixa só saímos a bolita 1 e vemos que está en estado | G>, xa sabemos que sen ter que saír da caixa, a bolita 2 estará en estado | G> (ver figura 2). Ten en conta que isto non é posible si as dúas bolitas están en dúas caixas, aínda que estean superpuestas. Neste caso, si salgue a primeira bolita e | G>, a segunda bolita pode ser | G> ou | Ou>. Non existe ningunha relación entre ambos.
Son moitos os estudos que se están levando a cabo sobre as dificultades. Tras complicar dous bolitas mantéñense complicadas ata que se realiza una medición, aínda que a distancia entre elas sexa moi grande. Sexa cal for a distancia, a medida nunha bolita actúa bruscamente sobre a outra bolita e cambia o seu estado aínda que non a tocamos. Aínda non sabemos por que e como se complica, pero xa somos capaces de utilizalo. Como se pode imaxinar, é a clave paira conseguir a teletransporte.
Telreporte cuántico
Temos dous bos amigos, Alaitz e Beñat, e un día xuntos decidiron complicar dous bolitas. Tras o enredo, cada un colleu o seu bolita nunha caixa especial, sen mirar nunca á bolita. Así, cando cada un trasladábase á súa casa, as dúas bolitas seguían enredadas, a pesar de estar afastadas.
Alaitz ten outra bolita na súa casa, metida noutra caixa, nun estado de superposición descoñecido. Alaitz, amante dos retos, pensa: "Como podo enviar a Beñat a nova bolita na situación na que se atopa sen moverche de casa? ". Non pode sacar a bolita da caixa, xa que neste caso cambiaría o seu estado natural a | G> ou | Ou>. El quere enviar a bolita a Beñat no seu estado natural, isto é, a | G> + b | Ou> en situación de superposición. Alaitzena parece un reto difícil, non?
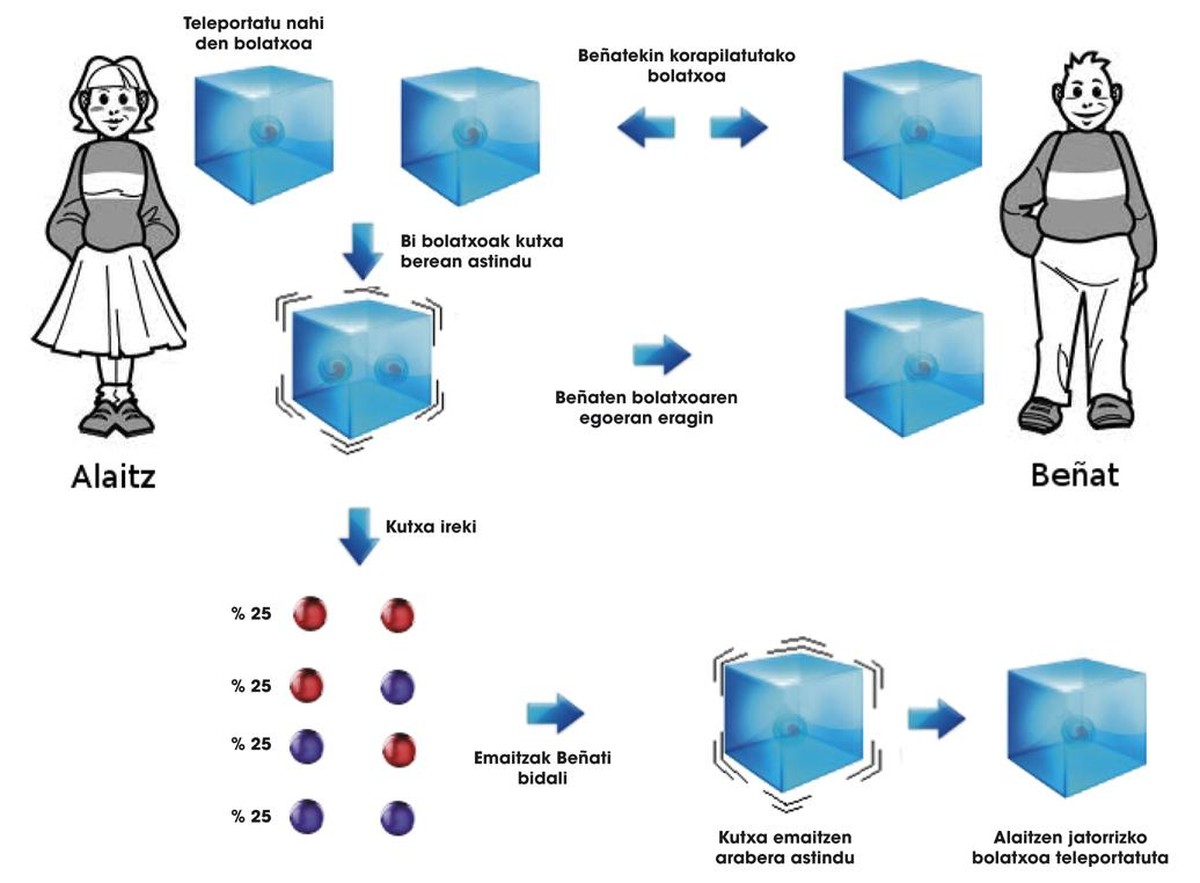
Pero como Alaitz é una moza intelixente, atopa una solución. A bolita que quere enviar a Beñat colócaa na mesma caixa coa que xa tiña enredada con Beñat. Lembra que Beñat ten o seu bolita gardada na súa casa. Alaitz realiza varias operacións nas dúas bolitas que ten nas súas mans, sacudindo a caixa dunha maneira especial. Como consecuencia do enredamiento, estas operacións tamén afectan á bolita de Beñat, e Alaitz sabe ademais a súa influencia. Por iso, abre a caixa paira coñecer o estado dos seus dous bolitas. As bolitas poden estar en estado | GG>, | GU>, | UG> ou | UU> respectivamente. Segundo o resultado, Alaitz coñece o estado da bolita de Beñat. Sorprendentemente, tras as operacións de Alaitz, estas posibles situacións son a | G> + b | Ou>, a | Ou> + b | G>, a | G> - b | Ou> e a | Ou> - b | G>.
Así que Alaitz, axiña que ve os seus dous bolitas, chámalle Beñat e dille como axita a caixa da súa bolita para conseguir a bolita que Alaitz quere enviar. Cuántica demostrounos que, sabendo como azoutar a caixa, das catro situacións que presentamos, pódese obter o estado orixinal da bolita de Alaitz. O proceso descrito pódese ver na figura 3. Ao final do proceso, a bolita de inicio de Alaitz foi telaudida en casa de Beñat!
É a teletransporte cuántica a teletransporte dos nosos soños?
A resposta breve a esta pregunta é negativa. Segundo a física actual, non se pode conseguir algo parecido á teletransporte de Star Trek. Por que? Que diferenzas hai entre a teletransporte cuántica que acabamos de ver e a de Star Trek?
1. Entre Alaitz e Beñat nunca se moveron bolitas: O estado da bolita inicial de Alaitz copiouse á bolita de Beñat, pero non houbo transporte de materia.
2. A teletransporte cuántico non é instantáneo. Para que se produza o teletransporte, Alaitz debe informar a Beñat da situación das súas dúas bolitas por teléfono, correo electrónico ou gritando. Esta comunicación pode producirse á velocidade máxima da luz pero non á velocidade. Por tanto, a telreporte cuántico necesita un tempo paira levar a cabo e non pode superar a velocidade da luz.
A pesar dos problemas, parece que, polo menos teoricamente, podemos conseguir que una persoa poida teletransportarse. Pero ten en conta as dificultades técnicas:
1. Paira levar una bolita de teletrabajo temos que ter outra na chegada (bolita de Beñat). Por tanto, temos que ter outras partículas na meta da persoa que queremos teletransportar.
2. As operacións e medidas deberían realizarse tendo en conta todas as propiedades das partículas dunha persoa. No caso das bolitas, só mencionamos a cor, pero as partículas cuánticas teñen moitas propiedades.
3. Deberiamos enviar toda a información destes millóns de medidas en destino utilizando as canles de comunicación habituais.
Iso é só o principio. En Cuántica xa se ha visto que é moi difícil manter o nó entre dúas partículas, que deben ser illadas do mundo. Por tanto, aínda que non se desprece do todo, podemos considerar case imposible que una persoa poida teletransportarse. Ademais, e pasando a un ámbito máis filosófico, é a mesma acode a que habemos teletransportado así? En definitiva, copiamos a información dunha persoa a outras partículas de materia. Deixamos a pregunta no aire.
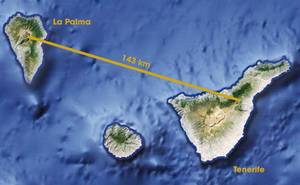
Con todo, coa tecnoloxía actual xa se conseguiu teletransportar fotóns e algúns átomos. No caso dos fotóns, conseguiuse a teladrinalización entre as illas de Tenerife e A Palma, impondo unha marca de 143 km (ver figura 4). As explicacións deste experimento foron publicadas na prestixiosa revista Nature en 2012. Pola súa banda, investigadores da Universidade de Maryland conseguiron en 2009 teletransportar un átomo a unha curta distancia.
Teletransporte hoxe e mañá
Dominamos a teletransporte cuántico a nivel teórico: coñécense as propiedades da mesma, sabemos como facelo e sabemos as súas limitacións. Tecnoloxicamente tamén se deron pasos moi importantes, tal e como explicamos. Estamos convencidos de que no futuro seremos capaces de teletransportar distancias máis longas e maiores cantidades de información, pero onde está o límite? Quen sabe.
A telreporte cuántico será una tecnoloxía moi importante no futuro. Imprescindible na criptografía cuántica, será una das claves no futuro paira a obtención de computadores cuánticos. Seguramente se utilizará en aplicacións que agora non podemos imaxinar, que en principio só existía no ámbito da ficción.
En Euskal Herria temos a honra de ser un grupo de investigadores punteiros nestes temas. O grupo Quantum Technologies for Information Science1, do Dr. Enrique Solano, que veu da man de Ikerbasque a Leioa, xa goza de gran prestixio internacional. Exemplo diso é o artigo publicado na revista Nature en 2010.
Aquí e alá, os investigadores achegarannos un novo coñecemento sobre o noso fascinante mundo. A telreporte cuántico ábrenos novas portas, pero ninguén pode saber que vai estar detrás delas. Como di Pedro Miguel Etxenike, o novo coñecemento aumenta o descoñecemento, xa que cada resposta expón mil novas preguntas.