Fikzioa errealitate bihurtzen denean
Ikertzailea eta irakaslea
Euskal Herriko Unibertsitateko Informatika Fakultatea
Kuantika, beti kuantika
Start Trek moduko telesailetan ikusi dugun teleportazio-motara gehien hurbiltzen den ideia zientifikoa teleportazio kuantikoa da, zeinaren helburua baita sistema kuantiko bat A puntutik B puntura garraiatzea, inolako euskarri edo kanal fisikorik gabe. Baina hori guztia behar bezala ulertzeko, fisika kuantikoaren oinarri batzuk azaldu behar ditugu. Ez izutu! Oso modu ulerterrazean egingo baitugu.
Kutxak eta bolatxoak
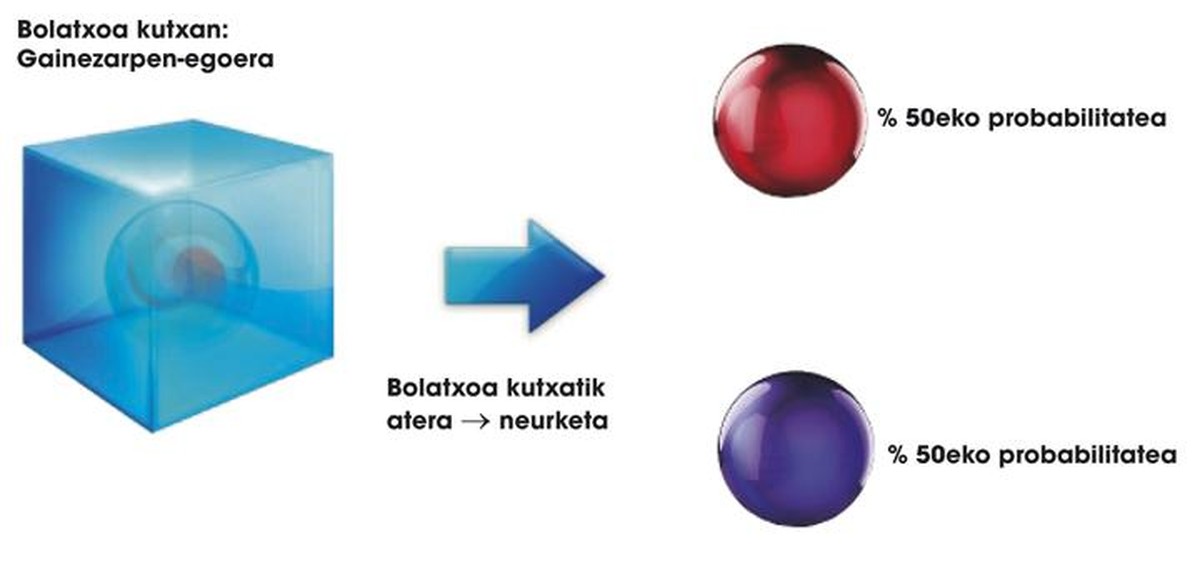
Sistema kuantikoak aipatzen ditugunean, atomo, elektroi, protoi edo fotoi moduko kontzeptuei buruz dihardugu. Gauzak erraztearren, kutxa berezi batzuetan gordeta dauden bolatxo berezi batzuk izango dira guretzat sistema kuantikoak. Bolatxo horiek bi kolore izan ditzakete: gorria |G> ala urdina |U> . Hona hemen bolatxo horien lehen berezitasuna: kutxaren barnean dauden bitartean, |G> eta |U> koloreen konbinazio-egoera batean egon daitezke:
a |G> + b |U>
non a eta b bi zenbaki erreal baitira. Horien esanahia sinplea da: kutxatik ateratakoan bolatxoak izango duen kolorearen probabilitatea adierazten dute. Hots, bolatxo bat 0,5 |G> + 0,5 |U> egoeran badago, kutxa irekitzean |G> izateko probabilitatea % 50 da. Kuantikan, gainezarpenaren propietate deritzo bolatxoen propietate horri. Horrek beste lege berezi batera garamatza: bolatxoak, kutxa barruan, gainezarpen-egoeran egon daitezke; baina, kutxa irekitzen dugunean, |G> ala |U> bakarrik izan daitezke. Kutxatik at ez dago gainezarpenik. Kutxa irekitzearen sinonimo kuantikoa neurketa da, non bolatxoen gainezarpen-egoera deuseztatzen baita (ikus 1. irudia).
Kutxak, ordea, ez dira bolatxoak gordetzeko bakarrik erabiltzen. Kutxa modu ezberdinetan astinduz gero, bolatxoaren egoera alda dezakegu, adibidez konbinazioen proportzioak aldatuz. Astintzearen baliokidea eragiketa kuantikoak dira. Mota askotakoak daude, eta guk ez dugu horretan sakonduko. Oraingoz, pentsatu kutxa astinduta gai garela nahi ditugun eragiketak egiteko.
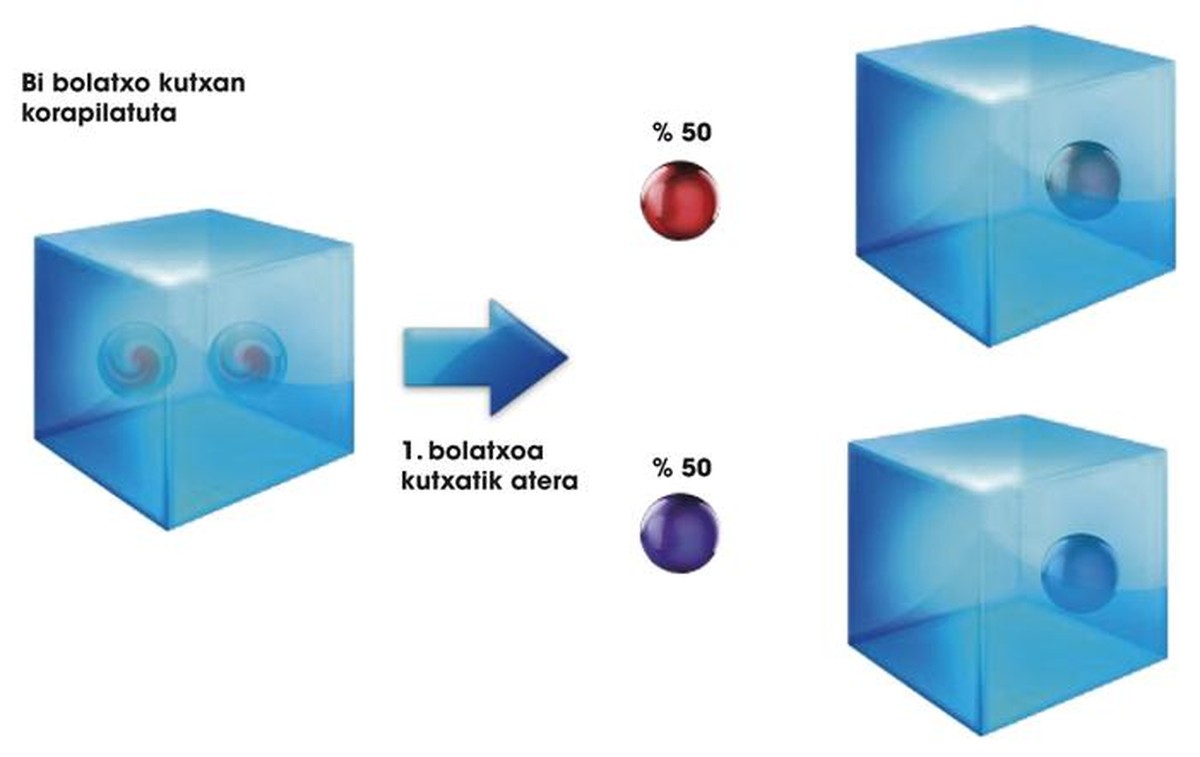
Atal honekin bukatzeko, gure kutxa eta bolatxoen beste berezitasun bat aipatu beharrean gaude. Bi bolatxo kutxa berean jartzen baditugu eta kutxa astintzen badugu, bolatxoak elkarrekin korapila ditzakegu. Hala, 1. bolatxoa eta 2. bolatxoa kutxa berean astinduta, 0,5 |G 1 G 2 > + 0,5 |U 1 U 2 > egoera lor dezakegu. Kuantikan, egoera horri korapilatze deritzo, bi bolatxoak elkarrekin korapilatuta geratzen baitira. Egoera horretan, kutxatik 1. bolatxoa bakarrik ateratzen badugu eta |G> egoeran dagoela ikusi, jada badakigu, kutxatik atera beharrik gabe, 2. bolatxoa |G> egoeran egongo dela (ikus 2. irudia). Kontu izan hori ez dela posible bi bolatxoak bi kutxatan izanez gero, nahiz eta gainezarrita izan. Kasu horretan, lehen bolatxoa atera eta |G> bada, bigarren bolatxoa |G> edo |U> izan daiteke. Bien artean ez dago inolako loturarik.
Azterketa asko ari dira egiten korapilatzeren gainean. Bi bolatxo korapilatu ondoren, neurketa bat egin arte korapilatuta mantentzen dira, nahiz eta haien arteko distantzia oso handia izan. Distantzia edozein delarik ere, bolatxo batean egindako neurketak beste bolatxoan eragiten du bat-batean, eta horren egoera aldatzen du, nahiz eta ez dugun ukitu ere egin. Oraindik ez dakigu zergatik eta nola gertatzen den korapilatzea, baina jada erabiltzeko gai gara. Pentsa daitekeen moduan teleportazioa lortzeko giltzarria dugu.
Teleportazio kuantikoa
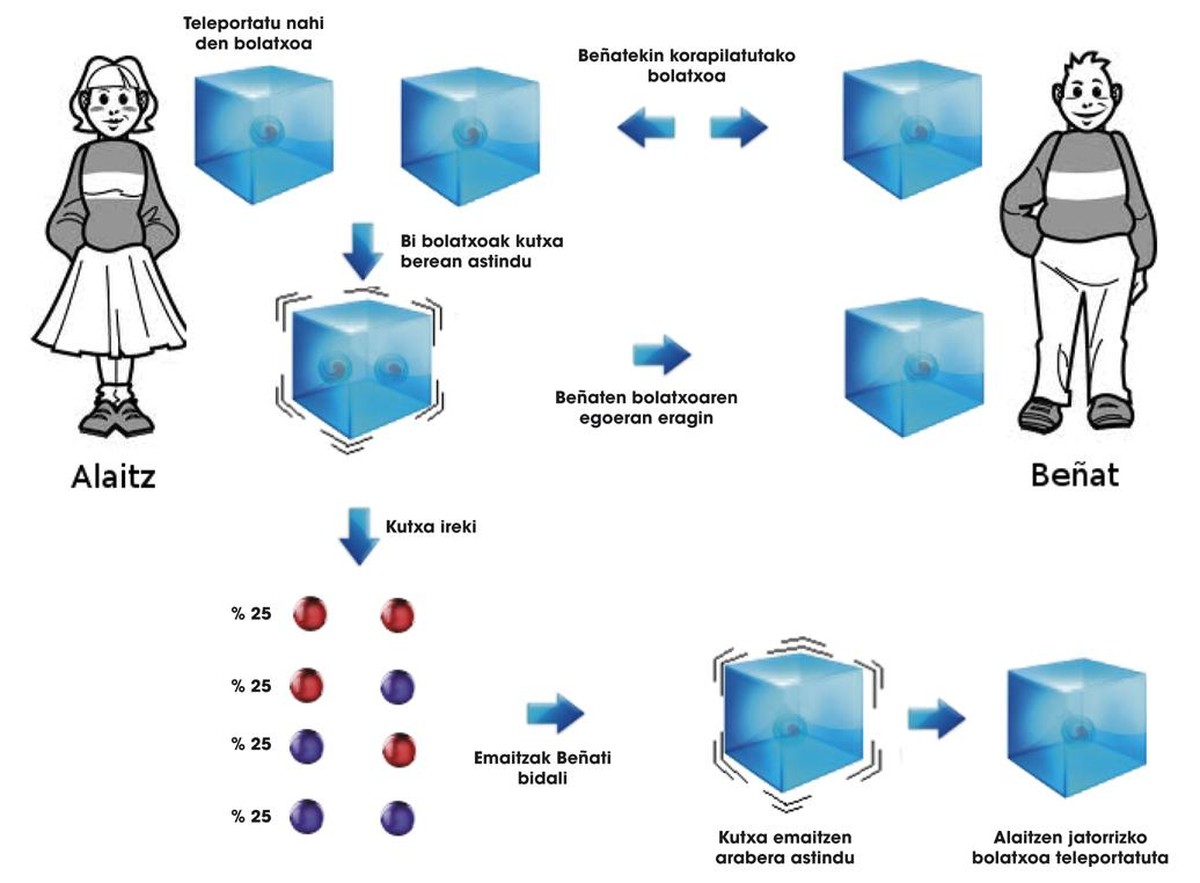
Alaitz eta Beñat bi lagun on ditugu, eta, elkarrekin zeuden egun batean, bi bolatxo korapilatzea erabaki zuten. Korapilatzea gertatu ondoren, bakoitzak bere bolatxoa hartu zuen kutxa berezi batean, bolatxoari inoiz begiratu gabe. Hala, bakoitza bere etxera joandakoan, bi bolatxoek korapilatuta jarraitzen zuten, nahiz eta elkarrengandik urrun egon.
Alaitzek beste bolatxo bat du etxean, beste kutxa batean sartuta, gainezarpen-egoera ezezagun batean. Alaitzek erronkak atsegin dituenez, zera pentsatu du: " Nola bidal diezaioket Beñati bolatxo berria, dagoen egoeran, etxetik mugitu gabe? ". Ezin du bolatxoa kutxatik atera, kasu horretan haren berezko egoera aldatuko bailitzateke, eta |G> ala |U> bihurtu. Berak berezko egoeran bidali nahi dio bolatxoa Beñati, hots a |G> + b |U> gainezarpen-egoeran. Erronka zaila dirudi Alaitzenak, ezta?
Baina Alaitz neska azkarra denez, topatu du konponbide bat. Beñati bidali nahi dion bolatxoa jada Beñatekin korapilatuta zeukan bolatxoarekin batera jarri du kutxa berean. Kontu izan Beñatek bere bolatxoa bere etxean gordeta duela. Alaitzek eragiketa batzuk egiten ditu eskuetan dituen bi bolatxoetan, kutxa modu berezi batean astinduz. Korapilatzearen ondorioz, eragiketa horiek Beñaten bolatxoari ere eragiten diote, eta Alaitzek badaki, gainera, zer eragin izan duten. Ondorioz, kutxa irekitzen du bere bi bolatxoak zer egoeratan dauden jakiteko. Bolatxoak |GG>, |GU>, |UG> edo |UU> egoeran egon daitezke, hurrenez hurren. Emaitzaren arabera, Alaitzek badaki Beñaten bolatxoa zein egoeratan dagoen. Harrigarria badirudi ere, Alaitzen eragiketen ondoren, egoera posible horiek a |G> + b |U>, a |U> + b |G>, a |G> - b |U> eta a |U> - b |G> dira.
Beraz, Alaitzek bere bi bolatxoak ikusi bezain pronto Beñati deitzen dio, eta esaten dio nola astindu behar duen haren bolatxoaren kutxa Alaitzek bidali nahi dion bolatxoa lortzeko. Kuantikak erakutsi digu ezen, kutxa nola astindu jakinez gero, aurkeztu ditugun lau egoera horietatik Alaitzen bolatxoaren jatorrizko egoera lor daitekeela. Azaldu dugun prozesua 3. irudian ikus daiteke. Prozesuaren bukaeran, Alaitzen hasierako bolatxoa Beñaten etxera teleportatu da!
Teleportazio kuantikoa al da gure ametsetako teleportazioa?
Galdera horren erantzun laburra ezezkoa da. Gaur egungo fisikaren arabera, ezin da Star Trek -eko teleportazioaren modukorik lortu. Zergatik? Zer ezberdintasun daude ikusi berri dugun teleportazio kuantikoaren eta Star Trek -ekoaren artean?
1. Alaitz eta Beñaten artean ez da inoiz bolatxorik mugitu: Alaitzen hasierako bolatxoaren egoera Beñaten bolatxora kopiatu da, baina ez da izan materia-garraiorik.
2. Teleportazio kuantikoa ez da bat-batekoa. Teleportazioa gerta dadin, Alaitzek Beñati bere bi bolatxoen egoeraren berri eman behar dio telefonoz, posta elektronikoz edo oihuka. Komunikazio hori, gehienez ere, argiaren abiaduran gerta daiteke, baina ez azkarrago. Beraz, teleportazio kuantikoak denbora-tarte bat behar du gauzatzeko, eta ezin du gainditu argiaren abiadura.
Arazoak arazo, badirudi teorikoki bederen lor dezakegula pertsona bat teleportatzea. Baina kontu izan zailtasun teknikoak:
1. Bolatxo bat teleportatzeko, beste bolatxo bat izan behar dugu helmugan (Beñaten bolatxoa). Beraz, teleportatu nahi dugun pertsonaren beste partikula batzuk izan behar ditugu helmugan.
2. Pertsona baten partikula guztien propietate guztiak aintzat hartuta egin beharko genituzke eragiketak eta neurketak. Bolatxoen kasuan, kolorea bakarrik aipatu dugu, baina partikula kuantikoek propietate asko dituzte.
3. Milioika neurketa horien informazio guztia bidali beharko genuke helmugan, ohiko komunikazio kanalak erabiliz.
Hori hasiera besterik ez da. Kuantikan jada ikusi da oso zaila dela bi partikularen arteko korapilatzea mantentzea, partikula horiek mundutik isolatu behar baitira. Ondorioz, guztiz arbuiatu gabe ere, ia ezinezkotzat jo dezakegu pertsona bat teleportatzea. Gainera, eta esparru filosofikoago batera pasatuta, pertsona bera al da horrela teleportatu dugun pertsona bat? Azken batean, pertsona baten informazioa beste materia-partikula batzuetara kopiatu dugu. Airean utziko dugu galdera.
Dena dela, gaur egungo teknologiarekin jada lortu da fotoiak eta atomo batzuk teleportatzea. Fotoien kasuan, Tenerife eta La Palma uharteen artean lortu zuten teleportazioa, eta 143 km-ko errekorra ezarri (ikus 4. irudia). Esperimentu horren azalpenak Nature aldizkari ospetsuan argitaratu ziren 2012. urtean. Maryland Unibertsitateko ikertzaile batzuek, bestalde, distantzia labur batean atomo bat teleportatzea ere lortu zuten, 2009. urtean.
Teleportazioa gaur eta bihar
Teleportazio kuantikoa maila teorikoan menderatzen dugu: teleportazioaren propietateak ezagutzen dira, badakigu nola egin eta badakigu zer muga dituen. Teknologikoki ere oso pauso garrantzitsuak eman dira jada, azaldu dugun moduan. Ziur gaude etorkizunean distantzia luzeagoak eta informazio-kopuru handiagoak teleportatzeko gai izango garela, baina non dago muga? Nork jakin.
Teleportazio kuantikoa oso teknologia garrantzitsua izango da etorkizunean. Kriptografia kuantikoan ezinbestekoa da, eta, etorkizunean, giltzarrietako bat izango da ordenagailu kuantikoak lortzeko ere. Ziurrenik, orain imajinatu ere ezin ditugun aplikazioetan erabiliko da, hasiera batean fikzioaren esparruan bakarrik zegoen bitxikeria hori.
Euskal Herrian, gai hauetan diharduen punta-puntako ikerlari-talde bat izateko ohorea dugu. Ikerbasquen eskutik Leioara etorri zen Enrique Solano doktorearen Quantum Technologies for Information Science1 taldeak jada sona handia du nazioartean. Horren adibide da 2010. urtean Nature aldizkarian argitaratu zuten artikulua.
Hemen zein han, ikerlariek gure mundu liluragarri honi buruzko ezagutza berria ekarriko digute. Teleportazio kuantikoak ate berriak irekiko dizkigu, baina inork ezin du jakin zer egongo den ate horien atzean. Pedro Miguel Etxenikek dioen moduan, ezagutza berriak ezjakintasuna areagotzen du, erantzun bakoitzak mila galdera berri azaleratzen baititu.
Bibliografia
Idatzi zuk zeuk Gai librean atalean
Gai librean aritzeko, bidali zure artikulua aldizkaria@elhuyar.eus helbidera
Hauek dira Gai librean atalean Idazteko arauak