Edith Clarke : le patrimoine d’une femme dans la science
Bien que peu savent, Edith Clark, la première ingénierie américaine, a inventé le Clark transformé, tellement utilisé dans l'étude des réseaux triphasés et des machines électriques pour simplifier les calculs. Cette transformation a entraîné la simplification des calculs nécessaires à l'étude des systèmes triphasés de réseaux électriques, puis des machines électriques.
Années initiales
Edith Clarke est né en 1883 dans le comté américain de Howard (Maryland). Après des études de mathématiques et d'astronomie, il a passé ses premières années de carrière dans l'enseignement. Plus tard, bien qu'il commence ses études de génie civil à l'Université du Wisconsin, il quitte George A pour travailler à l'American Telephone and Telegraph. Assistant de l'ingénieur Campbell. A cette époque, sans ordinateurs, les quelques femmes consacrées à la science travaillaient comme des « ordinateurs humains ». Autrement dit, sa principale obligation était de réaliser des calculs complexes et longs. Cependant, Edith Clark a brisé les limites de l'époque en faisant partie du projet de construction de la première ligne téléphonique transcontinentale de New York à la Californie. L'expérience acquise en travaillant sur les circuits électriques et les lignes de transmission et la passion qu'il avait pour son travail en général l'a amené à réaliser des études d'ingénierie électrique. Ainsi, il a étudié au Massachusetts Institute of Technology (MIT), étant la première femme à recevoir ce diplôme au MIT.
Cependant, avec cette qualification du MIT, il n'a pas non plus atteint le même statut professionnel que les hommes ingénieurs. En fait, en 1920, il est entré dans General Electric (GE), où il a dirigé un groupe de «femmes ordinateurs» qui calculaient les tensions mécaniques des turbines et des rotors. Enfin, en 1923, après deux ans comme professeur à l'Université d'Istanbul, elle retourne à GE et devient la première ingénieure électrique des États-Unis. À son tour, il a rejoint l'American Institute of Electrical Engineers, brisant les deux autres frontières féminines de l'époque. D'une part, elle a été la première femme à publier un article scientifique (Steady-state stability in transmission systems-calculation by means of equivalent or circle diagrams) et, d'autre part, la première femme ayant droit de vote complet.
Edith Clarke a travaillé à GE jusqu'en 1945 et entre 1947 et 1956 enseigné à l'université du Texas jusqu'à sa retraite. Tout au long de sa carrière professionnelle, il a obtenu diverses choses dans le domaine de l'électricité et des lignes de transmission. Entre autres, il a proposé des circuits équivalents qui peuvent être utilisés pour étudier la stabilité des systèmes de puissance et a publié une étude sur les lignes de transmission de plus de 300 milles de longueur. En outre, des années plus tard, en 1943, il publie le livre Circuit analysis of A-C power systems et publie plusieurs articles scientifiques avec le chercheur Charles Concordia, entre autres. La transformation qui porte son nom dérive de son travail avec Charles Concordia: Clarke transformé. Cette transformation mathématique consiste à transformer les systèmes électriques triphasés en un système à deux dimensions indépendantes, facilitant la complexité des calculs. Actuellement, en plus des lignes de transmission, il existe d'autres applications dans lesquelles cette matrice de transformation est très utilisée (figure 2).
Clarke transformé et réseau électrique
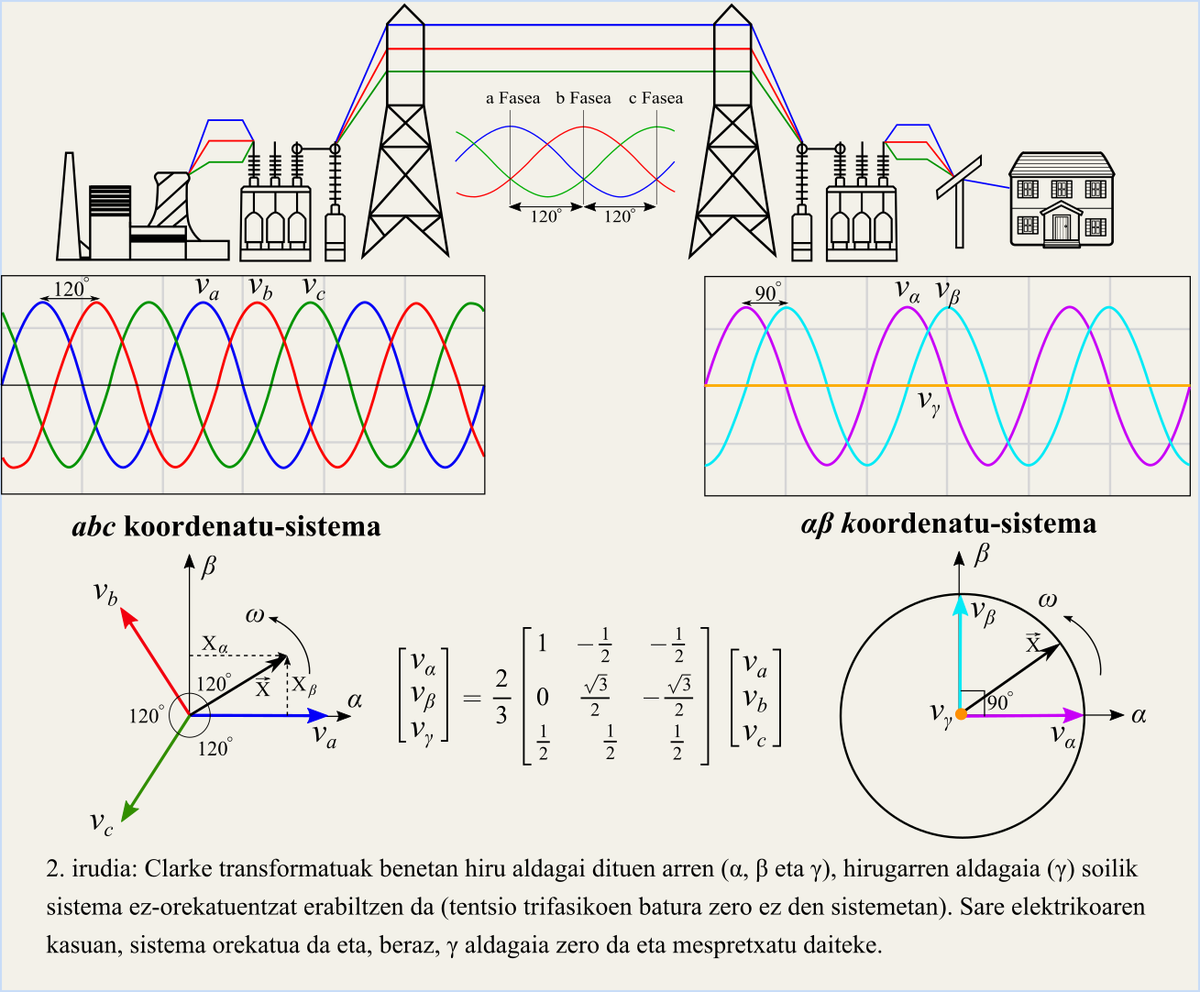
Le réseau électrique actuel est triphasé, c'est-à-dire composé de trois signaux sinusoïdaux avec un décalage de . XX. Au début du XXe siècle, le calcul des longues lignes de transmission du réseau électrique était très complexe, notamment en raison de la nécessité de réaliser tous les calculs manuellement. La matrice de transformation proposée par Edith Clark a considérablement simplifié l'analyse de ces systèmes. En fait, le système triphasé (coordonnées a, b, c) avec un décalage entre eux, convertit les systèmes stables à deux dimensions (coordonnées ?, b) avec un décalage de . Ce système résultant de la transformation est représenté par le fasor qui décrit le cercle radio de la tension du réseau électrique (Figure 2), dont la vitesse de rotation est égale à la fréquence du réseau électrique (Figure\ 2).
Malgré ce qui précède, il convient de noter que le système bidimensionnel obtenu après la transformation conserve toutes les informations que le système triphasé contenait, à savoir les variables ? et b stockent toutes les informations des variables a, b et c. Mais comment est-il possible ? Cela s'explique par une condition indispensable que rencontrent les réseaux électriques : le système triphasé doit être nécessairement équilibré. Un système équilibré signifie que la somme instantanée des trois tensions est zéro. Ainsi, en représentant les variables a, b et c comme vecteurs (figure 2), leur somme est zéro. Cette condition garantit que deux variables système sont connues et la troisième. D'autre part, cette transformation a une autre caractéristique intéressante. En effet, le décalage entre ? et b n'est pas aléatoire, car ce décalage garantit que les deux variables sont indépendantes les unes des autres. Ainsi, les modifications apportées à a ne se refléteront pas dans et vice versa.
Clarke transformé en applications actuelles
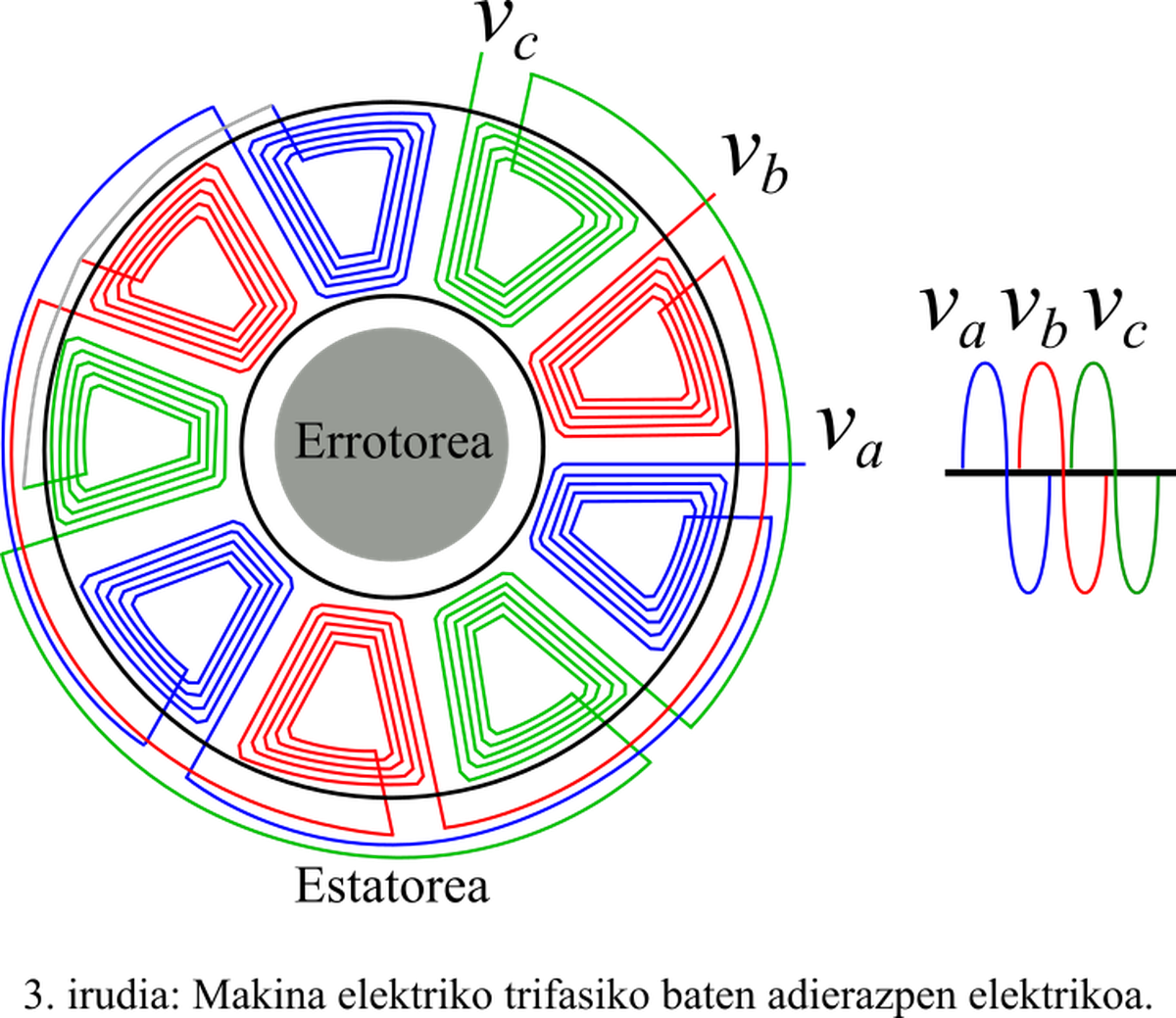
Bien que le réseau triphasé soit un bon exemple d'application dans laquelle Clarke est utilisé transformé, ses applications vont au-delà. Entre autres, nous pouvons souligner le contrôle utilisé sur les machines électriques. Les machines électriques peuvent être constituées de trois phases ou plus. Cependant, le système le plus simple est le triphasé, qui est celui qui sera pris comme modèle. Cependant, au lieu d'avoir trois lignes de transmission, la machine électrique se compose de trois bobines avec décalage de , connectées au même point (Figure 3). En outre, le transformé peut être utilisé avec la tension, le courant et le flux des machines.
Comme indiqué, cette transformation apporte deux variables indépendantes les unes des autres. Ceci est très important dans le contrôle des machines électriques, car il permet de contrôler de manière distribuée le flux magnétique et le moment de la machine. En ajoutant une petite explication, la première de ces variables représente le courant du stator (partie qui ne tourne pas en machine) de la machine électrique génératrice du flux magnétique. L'autre variable indique le courant du rotor (partie tournant sur la machine). Ce dernier est le courant qui génère de la force pour faire tourner l'axe de la machine électrique. En définitive, ces transformations visent à transformer le comportement d'une machine électrique AC en comportement d'une machine électrique DC, beaucoup plus simple. En résumé, la transformation de Clarke transforme trois variables connectées entre elles en deux variables indépendantes nécessaires pour contrôler la machine électrique. De cette façon, le contrôle des machines triphasés peut être effectué de la même manière que les machines DC, diminuant considérablement leur complexité.
Enfin, l'essor connu au cours de la dernière décennie par les machines électriques de haut niveau de puissance a fait que les machines polyphasés (plus de 3 phases) ont été utilisés dans de plus en plus d'applications. Bien que le clarke transformé ait été conçu pour être utilisé dans des systèmes triphasés, avec une petite transformation peut être facilement adapté aux machines polyphasés. Ainsi, grâce au travail de cette femme de nombreux ingénieurs, physiciens, mathématiciens et chercheurs peuvent résoudre des calculs complexes dans leur vie quotidienne en transformant Clarke.
Références
[1] James E. Brittain (1985). From Computor to Electrical Engineer: The Remarkable Career of Edith Clarke. IEEE Transaction on Education, vol. E-28, pp. 184-189.
[2] Tony Furfari. Women in Electrical Engineering.
[3] R. Clarke (1926). Steady-state stability in transmission systems calculation by means of equivalent circuits or circle diagrams. Journal of the A.I.E.E., vol. 45, pp. 365-373.
[4] Edith Clarke Biography: Biography Books (2019).