Edith Clarke: el patrimonio de una mujer en la ciencia
Aunque pocos saben, Edith Clark, la primera ingeniería de Estados Unidos, inventó el Clark transformado, tan utilizado en el estudio de redes trifásicas y máquinas eléctricas para simplificar cálculos. Esta transformación supuso la simplificación de los cálculos necesarios para el estudio de los sistemas trifásicos de redes eléctricas, y posteriormente de las máquinas eléctricas.
Años iniciales
Edith Clarke nació en 1883 en el condado estadounidense de Howard (Maryland). Tras los estudios de Matemáticas y Astronomía pasa sus primeros años de carrera en la enseñanza. Posteriormente, aunque inicia sus estudios de ingeniería civil en la Universidad de Wisconsin, abandona George A para trabajar en la American Telephone and Telegraph. Ayudante del ingeniero Campbell. En aquella época, al no haber ordenadores, aquellas pocas mujeres dedicadas a la ciencia trabajaban como "ordenadores humanos". Es decir, su principal obligación era realizar cálculos complejos y largos. Sin embargo, Edith Clark rompió los límites de aquella época formando parte del proyecto de construcción de la primera línea telefónica transcontinental de Nueva York a California. La experiencia adquirida al trabajar en circuitos eléctricos y líneas de transmisión y la pasión que tenía por su trabajo en general le llevaron a realizar estudios de ingeniería eléctrica. Así, estudió en el Massachusetts Institute of Technology (MIT), siendo la primera mujer en recibir este grado en el MIT.
Sin embargo, con esta titulación del MIT tampoco logró el mismo estatus profesional que los hombres ingenieros. De hecho, en 1920 entró en General Electric (GE), donde lideró un grupo de "mujeres computadoras" que calculaban las tensiones mecánicas de turbinas y rotores. Finalmente, en 1923, tras dos años como profesora en la Universidad de Estambul, regresa a GE y se convierte en la primera ingeniera eléctrica de Estados Unidos. A su vez, se incorporó al American Institute of Electrical Engineers, rompiendo las otras dos fronteras femeninas de la época. Por un lado, fue la primera mujer en publicar un artículo científico (Steady-state stability in transmission systems-calculation by means of equivalent circuits or circle diagrams) y, por otro, la primera mujer con derecho a voto completo.
Edith Clarke trabajó en GE hasta 1945 y entre 1947 y 1956 impartió clases en la universidad de Texas hasta su jubilación. A lo largo de su carrera profesional, consiguió diversas cosas en el campo de la electricidad y las líneas de transmisión. Entre otros, propuso circuitos equivalentes que pueden utilizarse para estudiar la estabilidad de los sistemas de potencia y publicó un estudio sobre líneas de transmisión de más de 300 millas de longitud. Además, años después, en 1943, publicó el libro Circuit analysis of A-C power systems y publicó varios artículos científicos con el investigador Charles Concordia, entre otros. La transformación que lleva su nombre deriva de su trabajo con Charles Concordia: Clarke transformado. Esta transformación matemática consiste en transformar sistemas eléctricos trifásicos en un sistema de dos dimensiones independientes entre sí, facilitando la complejidad de los cálculos. En la actualidad, además de en las líneas de transmisión, existen otras aplicaciones en las que esta matriz de transformación es muy utilizada (Figura 2).
Clarke transformado y red eléctrica
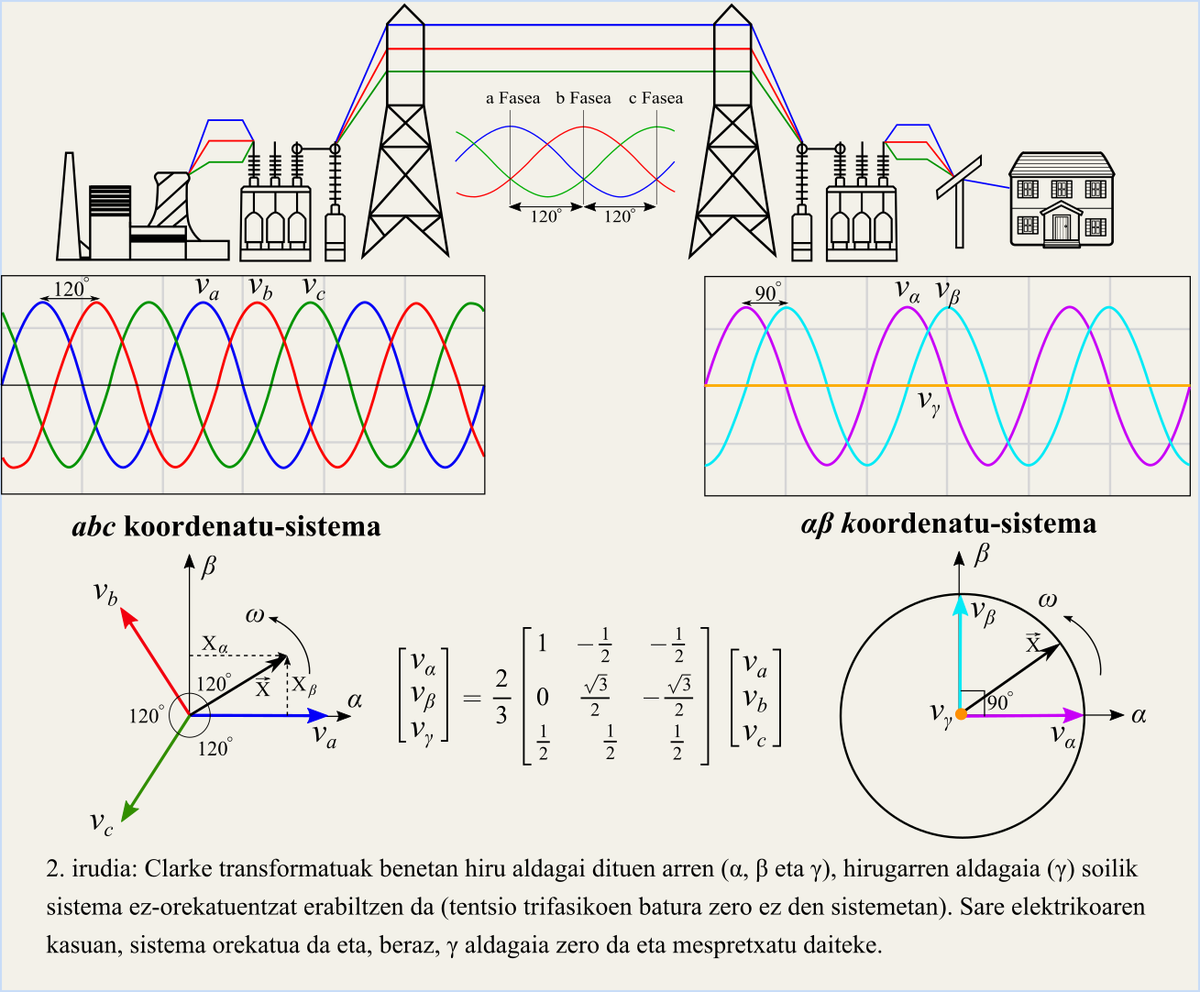
La red eléctrica actual es trifásica, es decir, está formada por tres señales sinusoidales con un desfase de . XX. A principios del siglo XX, el cálculo de las largas líneas de transmisión de la red eléctrica era muy complejo debido, entre otras razones, a la necesidad de realizar todos los cálculos manualmente. La matriz de transformación propuesta por Edith Clark simplificó notablemente el análisis de estos sistemas. De hecho, el sistema trifásico (coordenadas a, b, c) con un desfase entre sí de, convierte a sistemas estables de dos dimensiones (coordenadas ?, b) con un desfase de . Este sistema resultante de la transformación se representa por el fasor que describe el círculo de radio de la tensión de la red eléctrica (Figura 2), cuya velocidad de giro es igual a la frecuencia de la red eléctrica (Figura\ 2).
A pesar de lo anterior, cabe señalar que el sistema bidimensional que se obtiene tras la transformación conserva toda la información que el sistema trifásico contenía, es decir, las variables ? y b almacenan toda la información de las variables a, b y c. Pero, ¿cómo es posible? Esto se explica teniendo en cuenta una condición indispensable que cumplen las redes eléctricas: el sistema trifásico debe ser necesariamente equilibrado. Un sistema equilibrado significa que la suma instantánea de las tres tensiones es cero. Así, al representar las variables a, b y c como vectores (Figura 2), su suma es cero. Esta condición asegura que dos variables del sistema son conocidas y la tercera. Por otro lado, esta transformación tiene otra característica interesante. En efecto, el desfase entre ? y b no es aleatorio, ya que este desfase garantiza que ambas variables sean independientes entre sí. De esta forma, los cambios realizados en a no se reflejarán en < y viceversa.
Clarke transformado en aplicaciones actuales
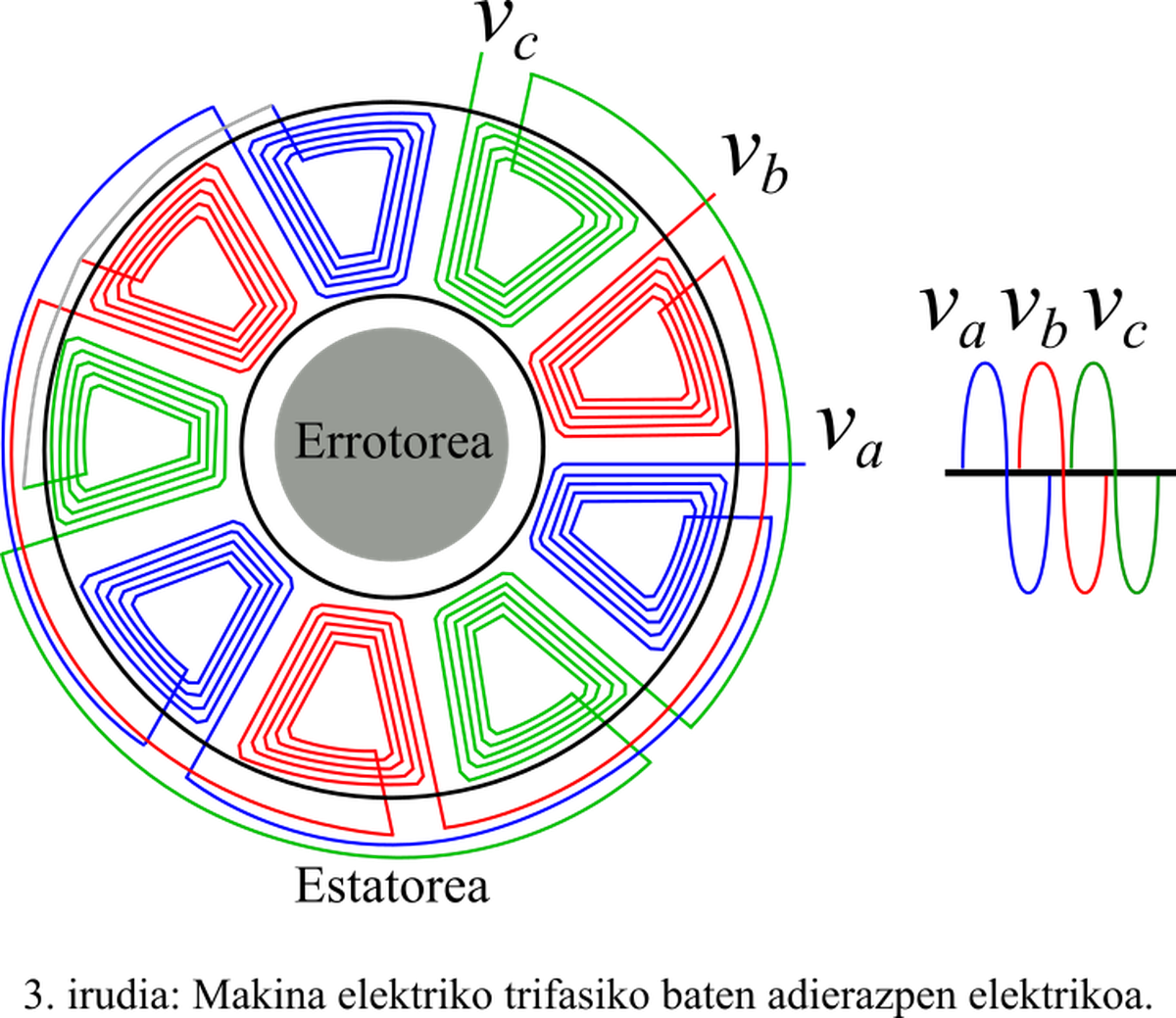
Aunque la red trifásica es un buen ejemplo de aplicación en la que se utiliza Clarke transformado, sus aplicaciones van más allá. Entre otros, podemos destacar el control que se utiliza en las máquinas eléctricas. Las máquinas eléctricas pueden estar formadas por tres o más fases. Sin embargo, el sistema más simple es el trifásico, que es el que se tomará como modelo. Sin embargo, en lugar de tener tres líneas de transmisión, la máquina eléctrica se compone de tres bobinas con desfase de , conectadas al mismo punto (Figura 3). Además, el transformado se puede utilizar con la tensión, corriente y flujo de las máquinas.
Como se ha comentado, esta transformación aporta dos variables independientes entre sí. Esto es muy importante en el control de las máquinas eléctricas, ya que permite controlar de forma distribuida el flujo magnético y el momento de la máquina. Por añadir una pequeña explicación, la primera de estas variables representa la corriente del estator (parte que no gira en máquina) de la máquina eléctrica generadora del flujo magnético. La otra variable indica la corriente del rotor (parte que gira en la máquina). Esta última es la corriente que genera fuerza para hacer girar el eje de la máquina eléctrica. En definitiva, estas transformaciones pretenden convertir el comportamiento de una máquina eléctrica AC en el comportamiento de una máquina eléctrica DC, mucho más simple. En resumen, la transformación de Clarke transforma tres variables acopladas entre sí en dos variables independientes necesarias para controlar la máquina eléctrica. De esta forma, el control de las máquinas trifásicas se puede realizar de forma similar a las máquinas DC, disminuyendo significativamente su complejidad.
Por último, el auge experimentado en la última década por las máquinas eléctricas de alto nivel de potencia ha hecho que las máquinas polifásicas (más de 3 fases) se hayan utilizado en cada vez más aplicaciones. Aunque el clarke transformado fue concebido para su uso en sistemas trifásicos, con una pequeña transformación se puede adaptar fácilmente a máquinas polifásicas. Así, gracias al trabajo de esta mujer muchos ingenieros, físicos, matemáticos e investigadores pueden resolver complejos cálculos en su día a día mediante la transformación de Clarke.
Referencias
[1] James E. Brittain (1985). From Computor to Electrical Engineer: The Remarkable Career of Edith Clarke. IEEE Transaction on Education, vol. E-28, pp. 184-189.
[2] Tony Furfari. Women in Electrical Engineering.
[3] R. Clarke (1926). Steady-state stability in transmission systems calculation by means of equivalent circuits or circle diagrams. Journal of the A.I.E.E., vol. 45, pp. 365-373.
[4] Edith Clarke Biography: Biography Books (2019).