Histoire des chiffres (V)
Déploiement du nouveau système
Le système indien a pris mille ans pour atteindre l'Europe, où les Arabes étaient des médiateurs.
L'expansion arabe (VIII-XIII. Au XIXe siècle, tous les peuples ont rassemblé des œuvres grecques, philosophiques, scientifiques ou littéraires et les ont arabisées. Partout, des bibliothèques et des universités ont été créées. Bagdad, Damas et plus tard les villes d'Alkairo, Kairuan, Fès, Grenade et Cordoue devinrent immédiatement des centres scientifiques.
En Europe XI. Jusqu'au XXe siècle, une crise politique et scientifique a été vécue. Par exemple, pour enseigner l'arithmétique théorique, le Nicomaco de Geresa (D.C.) II. siècle XX), inspiré par un travail mathématique lâche du grec Boèce (d.C.) Au Ve siècle, on utilisait une œuvre attribuée au latin. Quant à l'arithmétique pratique, contrôlaient la numérotation romaine et l'abaque.
Les Arabes, au début, assimilèrent la numérotation alphabétique grecque et hébrane et l'adaptèrent à l'alphabet de ses 28 lettres. D'autre part, il a récupéré le système de position sexagésimale et le zéro des Babyloniens. Mais quand ils ont connu le système indien à travers les relations commerciales, ils l'ont fait dans son intégralité.
Les Arabes n'y restèrent pas et apportèrent à la culture. Lors de la collecte et la traduction des travaux anciens, quelques commentaires ont été faits. En outre, la rigidité de la systématisation des mathématiciens grecs a été associée à la praticité de la science hindoue.
Parmi les mathématiciens arabo-islamiques se distingue le samanais Mohamed Ibn Mussa al-Khowarizmi (780-850). Il est connu pour ses deux livres. Dans la première, on parle d'arithmétique et on y explique le système indien avec des exemples. Elle s'ouvrirait ensuite avec succès en Europe occidentale. En fait, le nom latin de l'auteur est devenu le synonyme du système. Dans son deuxième travail, il a traité la science algébrique. Il a également été célèbre. Le titre de ce travail commençait par le mot alj. Une des deux opérations changeant de section les limites pour laisser des limites positives en deux parties d'une équation s'appelle :
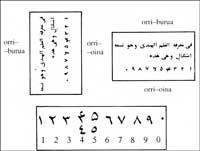
Quand les Arabes conquirent le système indien, ils ne firent que copier les chiffres. Après avoir passé par les mains des copistes, ils changèrent d'aspect.
Un motif de changement apparent se trouve dans l'écriture, car ils ont écrit par des colonnes, de gauche à droite. Ils lui donnaient un tour de 90° pour lire, dans le sens des aiguilles de l'horloge. Cependant, ce sont des chiffres qui ont été diffusés dans les provinces arabes et qu’ils appelaient «hindi».
Mais nos chiffres ne proviennent pas directement de celles-ci, mais de celles des Arabes occidentaux. IX. Au XVIIIe siècle, l'empire arabo-musulman fut brisé, en dehors du califat de Bagdad, de l'Afrique du nord-ouest et de la région musulmane de la péninsule ibérique. Cependant, les relations ne se sont pas rompues, surtout par des pèlerinages jusqu'à La Mecque, des échanges commerciaux, des guerres et des migrations de population. Les Arabes orientaux ont enseigné aux Occidentaux le système indien. Dans cette région, les chiffres ont évolué différemment.

Ces chiffres étaient appelés “ghobares” (chiffres en poudre) par la poussière qui se dispersait pour pouvoir écrire les chiffres dans les tables de calcul. Ce changement apparent est dû à la forme graphique des copistes occidentaux.
Pendant que les Arabes connaissaient le système indien, il fallut des siècles pour que les Européens l'acceptent. Dans l'Europe de l'époque, de l'abolition de l'Empire romain à la fin du Moyen Age, le calcul (calcul par abaque) était entre les mains de privilégiés. Cependant, les Occidentaux pouvaient obtenir les avantages du système hindou grâce au moine Gerbet d’Aurillac, qui en 999 fut nommé pape Silbestre II. Au couvent Gerbert a étudié les mathématiques et l'astronomie. Pendant son séjour dans la péninsule ibérique, il a étudié le système de numérotation et les méthodes de calcul des Arabes. En tant que directeur de l'école diocésaine de Reims, il a essayé d'appliquer ses études. Mais malheureusement, il n'a réussi qu'à introduire des chiffres (sauf zéro). Dans les abaques de colonne, les chants ont été remplacés par des chiffres, mais dans ces abaques, le zéro n'était pas nécessaire.
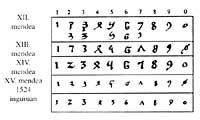
Comme pour les Arabes, en Europe, les chiffres ont été déformés pour différentes raisons, par écrit de fantaisie, par copie en bas ou indirectement, etc.
Après le passage des croix, les graphiques d'origine ont été récupérés. XIII. et XIV. À partir du XVIe siècle, il est devenu l'image actuelle. L'imprimerie de Gutenberg a fixé pour toujours les formes des chiffres. Bien que l'objectif des croisades n'était pas la reconquête de la science et de la culture, il a été l'un des résultats. Les croisés qui se sont dirigés vers la Terre Sainte sont revenus avec la culture locale. Les croisés ont eu des échanges commerciaux et culturels avec les musulmans. Grâce à eux, le système indien est entré en Europe.
De l'autre côté de la mer Méditerranée, dans la péninsule ibérique, XI. Depuis la fin du XXe siècle, les échanges culturels se renforcèrent grâce aux œuvres des traducteurs. Les chrétiens commencèrent alors à traduire tous les travaux en latin.
Dans cet environnement a souligné un mathématicien italien: Léonard de Pise, appelé “Fibonacci”. Il a étudié le système arabe en Afrique musulmane et au Moyen-Orient. Plus tard, en 1202, il a présenté le travail Liber Abaci (Traité d'abaque), dans lequel il a expliqué les règles du calcul des chiffres. Désormais, les supporters du nouveau calcul se multiplièrent. Cependant, le développement était loin.
Il y avait deux raisons principales pour que le nouveau calcul ne soit pas approuvé. D’une part, les “propriétaires” de l’ancien calcul voyaient leur vie périr. D'autre part, l'Eglise existait, qui a demandé que le développement de la science dépend de ses dogmes. La facilité de calcul des Arabes a été accusé à Satan.
L'étymologie zéro et les chiffres nous aideront également. Le mot zéro vient du mot sanscritique sifr (hutsa, hinduen sunya). Fibonacci, qui dans son travail Liber Abaci l'a appelé zephirum, plus tard il est devenu cefiro et à partir de 1491 il est resté zéro. Mais du mot sifr vient aussi le mot chiffre. Ses transcriptions en latin Sifra, Chiffre, Cyfra, Tzyphra, Cifre, Cyfre, etc. sont. Au début, ce mot avait la signification de zéro. Pour le comprendre, il faut revenir à l’environnement qui marque l’Église. L'utilisation de chiffres arabes était interdite à son époque. D'autre part, les gens utilisaient le système caché et ont commencé à se nommer «chiffre», mélangeant les deux significations (zéro et chiffre). Les experts ont essayé de maintenir leur signification originale, mais ils ne l'ont pas obtenu.
Les scientifiques se sont immédiatement montrés en faveur du nouveau système. Les commerçants, banquiers, fonctionnaires et en général arriérés ont du mal à abandonner l'abaque. Situation pendant le Moyen Age et la Renaissance XVII. et XVIII. Il est resté dans les administrations jusqu'au 20ème siècle.
C'est fini ?
Enfin et après une longue histoire d'obstacles, notre système a été achevé. Mais l'histoire des chiffres est-elle terminée ? Au moins, nous le croyons. Malgré le changement de la graphie des chiffres lorsque les ordinateurs apparaissent, son nom n'a pas bougé. Nous pourrions penser à d'autres bases comme 12 ou 2 (celles des ordinateurs). Cependant, le système ne changerait pas. Le principe de position, le zéro et les règles de calcul subsisteraient.
Depuis l'époque de l'homme Crô-Magnon jusqu'à l'homme moderne, il n'y a pas eu de changements fondamentaux dans le cerveau, mais une richesse culturelle. Le mathématicien Leopoldo Kronecker dit: « Dieu a créé le nombre naturel, le reste de l’œuvre humaine ». Ou dans les mots du philosophe allemand Lichtenberg: « L’homme a commencé dès le début : toute grandeur est égale à elle-même, et il a mesuré le soleil et les étoiles. »
La théorie de la visite des êtres d'autres mondes a échoué dans ce domaine. Si elles étaient si rapides, pourquoi ne pas nous laisser la numérotation de position et le zéro?
En chiffres, il n'y a pas de tour de Babel. Alors que dans le monde entier il ya plus de quatre mille langues et des dizaines d'alphabets, aujourd'hui, tous les peuples ont accepté le système de chiffres hindoue.
Ce système a permis la création et le développement de calculatrices et le traitement de l'information. Cela n'aurait pas été possible avec d'autres systèmes. Au début Léonard de Vinci, Pascal, Leibniz, Babbage,... (mécanique) plus tard Hallerith, Torres Quevedo, Arken,... (électromécanique) et finalement Turing, Atanasoff, Von Neumann,... Cela est dû au travail accompli par les scientifiques (électronique).
À côté des chiffres, il a développé le concept numérique et l'écriture mathématique.
Pendant longtemps on ne pouvait pas écrire des nombres négatifs, ni des références comme 4 - 7. Le concept zéro a donné cette chance.
Une autre réalisation a été de définir et d'unir des concepts différents. Par exemple, les fractions. Ils sont connus depuis l'antiquité. Les egypti ne connaissaient que les fractions originales (quand le numérateur est 1). Les Babyloniens ont donné aux fractions une rédaction rationnelle, créant des fractions sexagésimales. Les Grecs, à l'impossibilité de leur numérotation alphabétique, adoptèrent le système babylonien. L'écriture moderne est due aux hindous et l'invention de la ligne aux Arabes.
Par la suite, la découverte des fractions décimales (lorsque le diviseur est la rétrocession décimale) a permis d'écrire des chiffres à droite de la virgule. En Europe, le premier était le Belge Simon Stevin, qui a écrit en 1582 713 (0) 7 (1) 9 (2) 4 (3) pour écrire le numéro 713,794. Dix ans plus tard, le Suisse Jost Bürgi écrivit 713 794. La même année, l'Italien Magini a remplacé la circonférence par un point par 713.794. Quant à la virgule d'aujourd'hui, le néerlandais Wilbord Snellius a inventé le XVII. début du siècle: 713,794. La rationalisation de l'écriture des fractions a facilité l'invention du système décimal de mesure.
a.C. VI. Avant le XXe siècle, les mathématiciens grecs connaissaient l'existence des nombres irrationnels: racines 2, racines 71, ... Les pythagoriciens ont essayé de cacher ces nombres (pour ne pas se fâcher aux dieux), mais sont ensuite apparus comme “immenses”. Cependant, en raison de défaillances dans les systèmes de numérotation n'ont pas été correctement définis. Les mathématiciens européens, profitant des progrès, ont réalisé qu'ils étaient des nombres décimaux inépuisables (dans lesquels aucun chiffre n'était répété). De cette façon, ils ont réussi à se différencier des nombres rationnels. Depuis, le concept de nombres algébriques et de nombres transcendants a émergé. Aujourd'hui se distingue:
- Nombre irrationnel: ce n'est pas la solution d'une équation avec un coefficient global de premier ordre: , e, erro 7, erro 10, …
- Nombre algébrique: solution d’un coefficient complet et d’une équation algébrique: Solutions des équations 2, erro 2, erro 7, ... x -2 = 0, x 2 - 2 = 0, x 3 - 7 = 0,...
- Nombre transcendant: coefficient total ou fractionné et non solution d'équation: , e, log 2, cos 25º,...
Bien que le nouveau système peut écrire n'importe quel nombre naturel, les scientifiques ont adopté une écriture spéciale: 1000 = 10 3 ; 100.000 = 10 5 ; 82765900000000000 - 827659 x 10 11 ou en utilisant l'écriture de la virgule mobile 8,27659 x 10 16 .
Avec le nouveau système, une question peut être posée: quel est le plus grand nombre que vous pouvez écrire? Cette question a donné lieu au concept de l'infini. Aujourd'hui, nous représentons l'infini avec le symbole. Il a été utilisé pour la première fois en 1655 par l'anglais John Wallis. Il faut distinguer le concept physique et mathématique de l'infini. La plus grande valeur mesurée physiquement a été 1042. C'est le nombre de protons et de neutrons qui existent dans l'univers entre autres choses.
Les mathématiciens sont allés plus loin et ont inventé des nombres transfinis. Le premier d'entre eux est 0 (aleph-zéro) (c'est la première lettre de l'alphabet hébraïque). Cela représente le nombre de nombres naturels, impairs, paires, rationnels, etc.
Les deux découvertes qui ont permis l'avancée de l'algèbre étaient le nouveau système de chiffres et l'écriture symbolique linéaire. Son inventivité (1591) est due à François Viète. Viète généralisé l'algèbre quand il a exprimé des nombres inconnus avec x, et,... Celui-ci libéra l'algèbre et la pensée des objets concrets et contribua à s'approcher du raisonnement abstrait.
En ce qui concerne les symboles, au Moyen Age le signe (-) a été appelé minus et le signe (+) più. Les mots ont été remplacés par ñ et p, jusqu'à ce que dans 1489 l'allemand Richard Widmann reconnu pour la première fois les symboles connus (+, -). En 1557 l'anglais Robert Receke a inventé le signe =, Thomas Harriot en 1631 dans les différences et les symboles, William Oughtred en x (multiplication) XVII. Au début du XXe siècle et (racine carrée), symbole (dérivé de la lettre R), a été créé par Christoph Rudolf en 1525.
Ici se termine cette petite histoire des chiffres, une petite partie de l'histoire générale de l'être humain.