History of figures (V)
Deployment of the new system
The Hindu system took a thousand years to reach Europe, where the Arabs were mediators.
Arab expansion (VIII-XIII. During the 19th century, all peoples gathered Greek, philosophical, scientific or literary works and arabiced them. Libraries and universities were created everywhere. Baghdad, Damas and later the cities of Alkairo, Kairuan, Fez, Granada and Cordoba immediately became scientific centers.
In Europe XI. Until the 20th century there was a political and scientific crisis. For example, to teach theoretical arithmetic, the Nicomaco of Geresa (d.C.) II. 20th century), inspired by a loose mathematical work by the Greek Boethus (d.C.) A work attributed to the Latin was used in the 5th century. As for practical arithmetic, they handled Roman numeration and abacus.
The Arabs, at first, assimilated the Greek and Hebran alphabetic numeration and adapted it to the alphabet of its 28 letters. On the other hand, the sexagesimal position system and the zero of the Babylonians were recovered. But when they knew the Hindu system through commercial relations, they did it in its entirety.
The Arabs did not stay in it and contributed to the culture. When collecting and translating the old works, some comments were made. Furthermore, the rigidity of systematization of Greek mathematicians was associated with the practicality of Hindu science.
Among the Arab-Islamic mathematicians stands out the Samanese Mohamed Ibn Mussa al-Khowarizmi (780-850). He is known for his two books. The first speaks of arithmetic and explains the Hindu system with examples. It would later open successfully in Western Europe. In fact, the author's Latin name became the synonym for the system. In his second work he dealt with algebraic science. He was also famous. The title of this work began with the word alj. One of the two trades that changed section terms to leave positive terms in two parts of an equation is called:
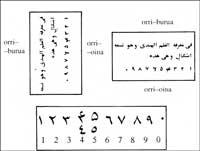
When the Arabs conquered the Hindu system, they did nothing but copy the figures. After passing through the hands of copyists they changed their appearance.
A reason for apparent change is found in writing, as they wrote by columns, from left to right. They gave him a 90° turn to read, clockwise. However, they were figures that spread throughout the Arab provinces and that they called “Hindi”.
But our figures do not come directly from these, but from those of the Western Arabs. IX. In the eighteenth century the Arab-Muslim empire broke, leaving out of the caliphate of Baghdad North West Africa and the Muslim region of the Iberian Peninsula. However, relations were not broken, especially by pilgrimages to Mecca, trade exchanges, wars and population migrations. Eastern Arabs taught Westerners the Hindu system. In this region the figures evolved differently.

These figures were called “ghobares” (powder figures) because of the dust that was spread to be able to write the figures in the calculation tables. This apparent change is due to the graphic form of western copyists.
While the Arabs knew the Hindu system, centuries had to pass for Europeans to accept it. In Europe of the time, from the abolition of the Roman Empire to the end of the Middle Ages, the calculation (calculation by abacus) was in the hands of privileged. However, the Westerners could obtain the advantages of the Hindu system thanks to the monk Gerbet d’Aurillac, who in 999 was named Pope Silbestre II. At the Gerbert convent he had studied mathematics and astronomy. During his stay in the Iberian Peninsula he studied the numeration system and calculation methods of the Arabs. As director of the diocesan school in Reims he tried to apply his studies. But, unfortunately, he only managed to introduce figures (except zero). In the column abacus the songs were replaced by figures, but in those abacus zero was not necessary.
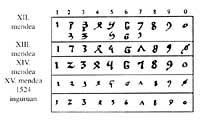
As with the Arabs, in Europe the figures were distorted for different reasons; for writing fantasy, for copying them face down or indirectly, etc.
After crossing the crosses the original prints were recovered. XIII. and XIV. From the sixteenth century it became the current image. The Gutenberg printing press forever fixed the shapes of the figures. While the aim of the crusades was not the reconquest of science and culture, it was one of the results. The Crusaders heading to the Holy Land returned with local culture. The Crusaders had commercial and cultural exchanges with the Muslims. Thanks to them the Hindu system entered Europe.
Across the Mediterranean Sea, on the Iberian Peninsula, XI. Since the end of the 20th century cultural exchanges were strengthened thanks to the works of translators. Then the Christians began to translate all the works into Latin.
In that environment, an Italian mathematician emphasized: Leonardo de Pisa, called “Fibonacci”. He studied the Arab system in Muslim Africa and the Middle East. Later, in 1202, he presented the work Liber Abaci (Treaty of Abaco), in which he explained the rules of the calculation of figures. From now on the fans of the new calculation multiplied. However, development was far away.
There were two main reasons for not approving the new calculation. On the one hand, the “owners” of the old calculation saw their life in danger. On the other hand, there was the Church, which called for the development of science to depend on its dogmas. The ease of calculation of the Arabs was accused of Satan.
The etymology of zero and figures will also help us. The word zero comes from the word sanscrítica sifr (hutsa, hinduen sunya). Fibonacci, who in his work Liber Abaci called him zephirum, later became cefiro and from 1491 remained zero. But from the word sifr also comes the word figure. His transcriptions in Latin Sifra, Cifra, Cyfra, Tzyphra, Cipe, Cyfre, etc. are. At first this word had the meaning of zero. To understand it, we must return to the environment that marks the Church. The use of Arab figures was banned in its day. On the other hand, people used the hidden system and began to call themselves “numbers,” mixing both meanings (zero and number). The experts tried to maintain its original meaning, but did not succeed.
Scientists immediately favored the new system. Traders, bankers, officials and in general backward had a hard time leaving the abacus. Situation during the Middle Ages and the Renaissance XVII. and XVIII. It remained in the administrations until the 20th century.
Is it over?
Finally, after a long history of obstacles, our system was completed. But has the history of the figures ended? At least we believe it. Despite changing the graph of the figures when computers appear, their name has not been moved. We could think of other bases such as 12 or 2 (computers). However, the system would not change. The position principle, zero and calculation rules would remain.
From the time of man Crô-Magnon to modern man there have been no basic changes in the brain, but cultural wealth. Mathematician Leopoldo Kronecker said: “God created the natural number, the rest human work.” Or in the words of the German philosopher Lichtenberg: “Man began from the beginning: every magnitude is equal to himself, and he came to measure the Sun and the stars.”
The theory of visiting beings from other worlds has failed in this field. If they were so fast, why didn't they leave us the position numbering and the zero?
In figures there is no tower of Babel. While around the world there are more than four thousand languages and dozens of alphabets, today all peoples have accepted the system of Hindu figures.
This system has allowed the creation and development of calculators and information processing. This would not have been possible with other systems. At first Leonardo de Vinci, Pascal, Leibniz, Babbage,... (mechanical) later Hallerith, Torres Quevedo, Arken,... (electromechanical) and finally Turing, Atanasoff, Von Neumann,... This is due to the work done by scientists (electronics).
Alongside the figures was developed the numerical concept and mathematical writing.
For a long time negative numbers could not be written, nor could remissions like 4 - 7. Concept zero gave that opportunity.
Another achievement has been to define and unite different concepts. For example, fractions. They have been known since ancient times. Egypti only knew the original fractions (when the numerator is 1). The Babylonians gave fractions a rational wording, creating sexagesimal fractions. The Greeks, faced with the impossibility of their alphabetic numbering, adopted the Babylonian system. Modern writing is due to the Hindus and the invention of the line to the Arabs.
Later, the discovery of decimal fractions (when the divisor is decimal reversal) allowed to write figures to the right of the coma. In Europe, the first was the Belgian Simon Stevin, who wrote in 1582 713 (0) 7 (1) 9 (2) 4 (3) to write the number 713,794. Ten years later the Swiss Jost Bürgi wrote 713 794. That same year the Italian Magini replaced the circumference with a point by 713,794. And as for today's coma, the Dutch Wilbord Snellius invented the XVII. beginning of the century: 713,794. The rationalization of the writing of fractions facilitated the invention of the decimal measuring system.
BC. VI. Before the twentieth century Greek mathematicians knew the existence of irrational numbers: roots 2, roots 71, ... The Pythagoreans tried to hide these numbers (not to get angry at the gods), but then appeared as “immense”. However, because of failures in numbering systems they were not defined correctly. European mathematicians, taking advantage of the advances, realized that they were inexhaustible decimal numbers (in which no figures were repeated). In this way they managed to differentiate themselves from rational numbers. Since then the concept of algebraic numbers and transcendent numbers emerged. Today it is distinguished:
- Irrational number: that is not the solution of any equation with a global coefficient of first order: , e, erro 7, erro 10, …
- Algebraic number: solution of a complete coefficient and an algebraic equation: Solutions of equations 2, erro 2, erro 7, ... x -2 = 0, x 2 - 2 = 0, x 3 - 7 = 0,...
- Transcendent number: total or fractional coefficient and no equation solution: , e, log 2, cos 25º,...
Although any natural number can be written in the new system, scientists have adopted a special script: 1000 = 10 3 and 100.000 = 10 5 and 82765900000000000 - 827659 x 10 11 or using mobile comma writing 8,27659 x 10 16 .
With the new system you can fill in a question: what is the largest number that can be written? This question gave rise to the concept of infinity. Today we represent infinity with symbol. It was first used in 1655 by the English John Wallis. The physical and mathematical concept of infinity must be differentiated. The highest physically measured value has been 1042. It is the number of protons and neutrons in the universe among other things.
Mathematicians have gone further and invented transfinite numbers. The first of them is 0 (aleph-zero) (it is the first letter of the Hebrew alphabet). This represents the number of natural, odd, even, rational numbers, etc.
The two discoveries that allowed the advance of algebra were the new system of figures and linear symbolic writing. His invention (1591) is due to François Viète. Viète generalized algebra when he expressed unknown numbers with x, and,... It liberated algebra and thought from concrete objects and contributed to approaching abstract reasoning.
As for the symbols, in the Middle Ages the sign (-) was called minus and the sign (+) più. The words were replaced by ñ and p, until in 1489 the German Ricardo Widmann recognized for the first time the known symbols (+, -). In 1557 the English Robert Receke invented the sign =, Thomas Harriot in 1631 in differences and symbols, William Oughtred in x (multiplication) XVII. At the beginning of the 20th century and (square root), symbol (derived from the letter R), was created by Christoph Rudolf in 1525.
Here ends this small history of figures, a small part of the general history of the human being.