La création de la science en Grèce : une école pythagoricienne

Bien que la tendance dominante de l'école ionienne était rationaliste, ce que les écoles pythagoriques ont été une tendance mystique dérivée de l'orfisme, qui se concentrait sur l'observation et la recherche.
Pitago (582-500 av. J.C.) naquit à Samos, mais vers 530 il se rendit en Italie du Sud.
Ceux de cette école ont cherché un principe d'intelligence qui est le créateur de l'Univers. En dehors de la tendance de l'école ionienne basée sur la transformation de la substance, cette école a établi que, à la base du monde matériel, la seule chose que l'esprit peut acquérir est le nombre.
Bien qu'avant la création de cette école, les Babyloniens adapté aux corps de pétrissage minutieux proportions numériques et Anaximadro lui-même a parlé de la salle neuf, dix-huit et vingt fois l'épaisseur du disque r, neuf, dix-huit et vingt fois plus, l'adaptation des nombres à tous les aspects de la nature est le résultat d'une école pythagoricienne.

Nous sommes habitués à utiliser l'idée des nombres (c'est-à-dire des quantités abstraites). Nous n'avons aucun problème dans cinq ou cent chiffres, indépendamment de ce qu'ils sont, pour pouvoir travailler. C'est pourquoi, tant pour la philosophie que pour les mathématiques, soyons conscients de la difficulté qu'il faut trouver et isoler l'unité des concepts du cinq ou du tissu dans des groupes de choses hétérogènes, c'est vraiment difficile.
Dans le domaine des mathématiques, cela a généré l'arithmétique. L'idée que la philosophie trouve le nombre à la base du monde réel. Aristote disait: "Il semble que le nombre est la base, c'est-à-dire la matière qui forme des choses réelles, selon les pythagoriciens". Ceux de Pythagore ont également travaillé en musique et ont vu qu'en donnant le quintette et octave d'une note de base dans ce domaine, ils se trouvaient dans des relations fixes de 6/4/3 de longueur d'une corde. L'idée que les entités de base étaient constituées d'unités définies et indivisibles a reçu une grande aide.
Alors, sur la base de ce schéma de nombres relatifs, ils voulaient construire toute la théorie de l'Univers. Ces nombres relatifs correspondaient à ces unités spatiales indivisibles. Ils considèrent que les distances entre les planètes et la Terre doivent suivre une progression musicale. Cela créerait la "musique des sphères".
Étant la somme des quatre premiers numéros, le dixième était un nombre parfait, de sorte que les corps de fusion devaient avoir aussi dix. Mais comme ils ne voyaient que neuf, ils lancèrent l'hypothèse d'un imprévu "contralur". Aristote a critiqué ce rêve par des actions.
Cependant, les pythagoriciens ont tenu la cosmogonie. La plupart de ce que nous savons à ce sujet, nous le savons à travers le Filolao de la tonne Kro. Il vivait au milieu du Ve siècle avant JC. Quelque part, ils ont réalisé que la Terre était sphérique et la rotation des cieux apparents était plus facile à exprimer si la rotation de la Terre était acceptée. Cette rotation de la Terre ne se produirait pas sur son axe mais sur un point fixe de l'espace, tournant le contre à l'autre extrémité du diamètre.

Cependant, comme dans cette rotation la moitié de la vie de la Sphère Terrestre est toujours du côté de la fusion extérieure, il n'est pas possible de voir la crête mentionnée. Au point fixe que l'on ne voit pas serait allumé un grand feu: l'"autel de l'univers". Cette idée a conduit à la création d'un erito erroné, de ce que les Pythagoriciens ont établi la théorie héliocentrique avant Aristarque et Copernic.
De la part de Kosmogonia Pitagora et de ses élèves ont abandonné l'idée d'un seul élément matériel pour reconnaître que la matière est formée par terre, eau, feu et air. Ces éléments constituaient une combinaison de quatre qualités par paires : chaleur, froid, humidité et sécheresse. Ainsi, tant que l'eau est froide et humide, le feu est chaud et sec.
Les premiers pas combinaient la géométrie avec l'arithmétique. Pitagora a enseigné basé sur l'abstraction, les définitions précises et les démonstrations. Si l'on considère les connaissances pratiques d'Egypo et de Mésopotamie, lignes, points, etc. Il est difficile de savoir quand et où sont apparues les idées abstraites; cependant, ces réalisations sont traditionnellement ajoutées aux pythagoriciens et avec eux la création de la géométrie abstraite. Cette école a démontré, entre autres, que les angles d'un triangle forment deux angles droits ou que sur le côté n les angles intérieurs d'un polygone de c (2n 4) servent d'angle droit.
La réalisation la plus connue du fondateur de cette école est le théorème baptisé "théorème de Pitagora": "Le carré construit avec l'hypotense d'un triangle droit est autant que des carrés construits par deux autres parties de ce triangle" (Euklide, "Eléments", I, 47).
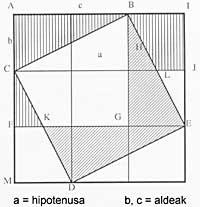
Plutarque, Diogene Laërce et Proklo affirment que ce théorème a été énoncé par Pitagora et que, en dehors de son origine originaire, apparemment connu par les Babyloniens, est l'une des bases les plus profondes de l'histoire des mathématiques.
L'idée mystique de la nature dans la doctrine des nombres dans cette école montre l'importance que les pythagore avaient des éléments opposés: la lumière et l'obscurité, l'amour et la haine, etc. Cette idée mystique est réapparue chez le médecin Alkmeon.
En ce sens, l'homme est un microcosme, c'est-à-dire un petit Univers : tandis que le corps reflète la structure du monde, l'âme est l'harmonie du nombre.
Si les Ioniens défendaient la philosophie de la matière, les pythagores défiaient la philosophie de l'apparence. a.C. Au cinquième siècle, cette dernière école a été divisée en deux branches: l'une est devenue une institution religieuse et l'autre a développé une théorie du nombre presque scientifique.





