Què és el so digital?
Què és el so digital? La resposta a aquesta pregunta és ràpida si sabem el que és el so. En definitiva, el so no és més que una ona que es propaga en l'aire, i digitalitzar el so és convertir aquesta ona en una successió de números. Aquesta seqüència es pot guardar i manipular en l'ordinador. El que oferia el cinema d'aquell país és, en definitiva, el resultat de tot això, almenys justificant així el preu de l'entrada.

Moltes vegades el preu de l'entrada assegura la qualitat digital del so. Però, què significa això? Per a respondre a aquesta pregunta hem d'analitzar els números anteriorment esmentats. Atès que la successió de números és l'expressió de l'ona, quants més números s'utilitzin per a un determinat interval de sons, millor expressió s'obtindrà. És clar, per tant, que aquest nombre de números ha de complir uns mínims.
Les ones de 440 Hz realitzen 440 cicles en un segon. I per a expressar correctament les oscil·lacions de l'ona és necessari prendre almenys 5 números per cicle. Per tant, es necessiten 2.200 números (2,2 kHz) per a poder expressar correctament aquest so. No obstant això, les freqüències més altes exigeixen un major nombre de números, per la qual cosa amb un determinat número els sons més freqüents estan menys representats que els menys freqüents.
Donades les característiques dels sons reals, s'ha adoptat 44,1 kHz com a estàndard de qualitat, és a dir, s'han de prendre 44.100 números per a mantenir un so d'un segon amb bona qualitat. No és massa per a l'equip d'aquell cinema?
Sons sonors, sons baixos
Un altre factor que ha de tenir-se en compte és que els valors que poden prendre aquests números també es reflecteixen en la qualitat. Per exemple, es pot utilitzar una escala de zero a deu, és a dir, una escala en la qual l'ona del so més sonor aconsegueix sovint el valor 10. Però aquesta escala no sol tenir una gran flexibilitat, és gairebé impossible distingir els matisos del so a través d'una petita escala. Per contra, l'escala utilitzada en el mercat és de -32.768 a +32.768.

Com s'ha triat un número tan estrany? Per l'expressió binària dels números. Aquest rang pot aconseguir un valor de 65.536, és el nombre de números que poden emmagatzemar 2 bytes en la memòria de l'ordinador.
Per tant, per a expressar correctament la intensitat del so, cada número necessita 2 bytes en la memòria i un so d'un segon necessita 44.100 números. Per tant, aquest so omplirà en la memòria 88.200 bytes, és a dir, uns 86 K. Es calcula que en la memòria d'un megaoctet només es poden emmagatzemar 11,89 segons. El so digital de baix perd qualitat, ja que 44,1 kHz i 2 bytes són les característiques ' de qualitat CD'.
Manipulació de números
No obstant això, independentment de la seva qualitat en CD, el so digital té altres característiques, ja que en tractar-se d'una successió de números és fàcilment manipulable. amb només canviar els números estem canviant el so. Per exemple, col·locant zeros en lloc de tots els números d'un interval de temps, convertim l'interval en silenci; o si dividim tots els números, reduïm el volum de l'interval a la meitat; etc. Encara que són canvis simples, les conseqüències són importants.

Al mateix temps, les complexes variacions dels números augmenten enormement les possibilitats de manipulació del so. Així, per exemple, es produeixen efectes sonors (ressons, distorsions, …), es redueix o elimina el soroll de fons continu, es reforcen diverses freqüències i s'afebleixen unes altres. D'altra banda, sovint produeixen un efecte similar al d'un canvi d'ubicació de les fonts sonores. Són molts els processos que es duen a terme abans de comercialitzar la música en un disc.
A més dels discos, els sons de la ràdio i la televisió estan manipulats digitalment. La veu, per exemple, està tractada per compressió. Aquest tractament estableix límits d'intensitat en el so, limitant així els senyals a partir d'una amplitud per a evitar els vèrtexs sonors bruscos. I tots ells són només alguns exemples de manipulació digital. El nombre d'oportunitats depèn de la creativitat. Per això, el so resultant i l'original no tenen molt a veure.

Tot el que escoltem en la televisió, la ràdio, el cinema i els discos és d'ordinador? No, clar, però l'ordinador és una eina molt útil per a manipular aquest so. En definitiva, es tracta d'una sèrie de números en els quals es pot canviar el so digital. I la seva qualitat depèn de la memòria que necessiti. En un CD, per exemple, s'emmagatzemen 44.100 números per segon, representats mitjançant 2 bytes cadascun.
Quan el cinema d'un poble perdut ofereix so digital, ens dóna el resultat d'aquest tractament i no el tractament. Per tant, no és el cinema el que necessita un ordinador amb gran memòria. Però el so ja no ens impressiona. Potser tenim raó de seduir-nos quan la imatge també és digital.
So, soroll organitzat
Una vegada acabat el dia a dia, descansar adequadament no és gens fàcil quan el veí està aprenent a tocar el violí. Sembla que el soroll que es produeix a l'altre costat de la paret superarà tots els obstacles per a evitar el nostre descans. No és d'estranyar, la física dels sons és un tema molt complex. Els fils del violí, agitats per les molècules de l'aire, produeixen ones de pressió. Aquestes ones provoquen la vibració de la paret i així es transmeten a l'aire de la nostra habitació. No hi ha forma senzilla d'evitar la transmissió, per la qual cosa l'assaig del veí serà obligatori. Si aprengués a tocar el contrabaix sikiera! Notícies
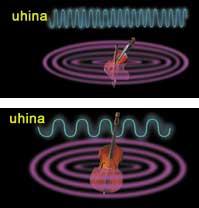
L'ona d'una 'la' donada pel contrabaix és només de 55 Hz. Les altes freqüències generen altes notes i les baixes notes. A més del violí del veí, un soprano que trenca cantant copes produeix ones d'alta freqüència. Però a més de crear la freqüència adequada, el soprano ha de cantar en veu alta per a trencar una copa.
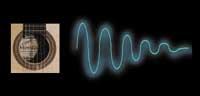
L'ona atenuada que es veu en la imatge, no obstant això, és ideal; les ones de sons reals són més complexes. Encara que escoltem una sola nota, les freqüències harmòniques intervenen en el so. A la freqüència bàsica s'afegeixen altres més grans, però no qualsevol freqüència, sinó múltiples de la bàsica. Això fa més complexa l'estructura de l'ona.
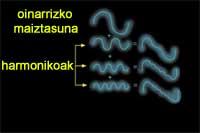
Cal tenir en compte els timbres, harmònics, freqüències i amplituds, no és massa per al veí? Mentre assaja, potser millor estar fos de casa. Al cap d'uns anys aprèn a controlar aquestes complexes ones. Utilitzarà les freqüències adequades per a la correcta execució de les notes i proporcionarà a cada nota la intensitat corresponent, controlant l'amplitud de l'ona. D'altra banda, s'utilitzarà el timbre d'altres instruments, donant més importància a unes freqüències harmòniques que a unes altres. Fins llavors, s'haurà de demanar al veí que insonoritzi l'habitació perquè l'ona no es transmeti en cap cas.
El teorema de Nyquist: clau per a digitalitzar
La digitalització del so real (una ona analògica) és un procés complex. En primer lloc, el micròfon rep la vibració de l'aire i el converteix en un senyal elèctric que després es digitalitza. Per a això, el so digital és una relació de mesures en les quals la tensió que canvia constantment. En un només segon poden ser milers de mesures.
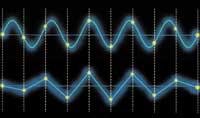
Per això, la qualitat de la digitalització dependrà del nombre de mesures adoptades per segon. L'estàndard d'enregistrament de CDs és de 44.100 mesures per segon. Per què? Com han arribat a aquest número? En definitiva, es tracta d'un càlcul matemàtic basat en el teorema de Nyquist.
Segons el teorema de Nyquist, per a expressar mitjançant números les ones d'una determinada freqüència, cada cicle ha de tenir almenys dues mesures. Per exemple, per a representar mitjançant números una ona de 5.000 Hz, necessitem com a mínim 10.000 números per segon.
En cas contrari, la declaració no serà adequada: Atès que en so real no existeix una freqüència única, aquesta regla s'aplica a la de menor longitud d'ona. D'altra banda, el so que pot sentir l'ésser humà no supera els 22.000 Hz, per la qual cosa l'estàndard de qualitat del so digital s'ha fixat en 44.100 Hz.
PC i Macintosh Antigament el so digital estava en mans d'uns pocs, però amb el desenvolupament dels ordinadors ha arribat també al consumidor del carrer. Els reproductors de música són cada vegada més barats, així com micròfons, gravadors, etc. Per tant, els estudis d'enregistrament amateur en llars privades s'estan convertint en una cosa habitual. En un estudi de casa és imprescindible l'ordinador per a poder treballar amb so digital. Hi ha molts bons programes disponibles, el límit actual és la grandària de la memòria, que també s'ha disparat en els equips domèstics. Aquest programari és capaç d'utilitzar un so de qualitat CD. L'estàndard d'arxius de so en PC és el d'extensió WAV i en Macintosh el d'extensió AIFF. Aquests arxius emmagatzemen, en definitiva, el so tal com s'explica en aquest article. No obstant això, perquè cada fitxer no compleixi tanta memòria, altres formats com el mp3 s'han convertit en habituals. No obstant això, en aquests formats alternatius la informació està comprimida, per la qual cosa els fitxers MP3 i AIFF tenen menor qualitat sonora que els fitxers MP3. |





