Ales de la papallona
Es pot dir, per tant, que la predicció meteorològica millorarà sense límits segons avança la ciència i la tècnica? Fem aquesta pregunta d'una altra manera: arribarem avui a imaginar amb precisió el clima de vuit o, més ben dit, a predir? Creiem que no. No n'hi ha prou amb avançar prou per a fer prediccions més precises. Creiem que factors intrínsecament immensos influiran en la predicció reduint la seva fiabilitat. Posem un exemple extrem.
Papallona del Carib

Quina influència té el vol d'un pinpilipaux en el litoral d'una illa del Carib en el temps? És a dir, en volar, el moviment de les ales sobre l'aire que està en contacte amb la papallona provoca una pertorbació. La pertorbació afectarà, en major o menor mesura, a l'aire circumdant en un moment o un altre. Aquest aire empenyerà el que té al seu costat i modificarà l'estat de l'aire en contacte amb ell, allargant la cadena d'efectes fins als cels del País Basc.
L'efecte del vol de la papallona serà a vegades menyspreable. I quant a les previsions d'un parell de dies, així serà, probablement, menyspreable. Prova d'això són les pròpies prediccions per a aquest període: hem dit que s'encerta en la majoria dels casos, almenys en condicions estables del cel. Diu que vindrà un front i ve, que ens bufarà el vent sud i ens tornem bojos l'endemà... Sembla que podem oblidar la papallona sense grans problemes.
Grau de rebuig

Sabem —perquè la ciència ha anat molt evolucionant— que en analitzar el moviment d'un camió no tenim per què tenir en compte a Einstein, Newton és suficient. “Calcularé els valors de les variables independents i les variables dependents. Si tinc la velocitat del camió i sé per on va, us diré el temps que trigarà encertant”. És a dir, la física clàssica és una eina molt útil amb camions. Som bastant deterministes en alguns àmbits: el llapis que tinc a la mà es deixa anar i em cau, no tenim cap dubte sobre aquest tema. Durant segles l'ésser humà ha evolucionat al llarg de la seva vida acompanyant a la física clàssica.
Els seus inicis eren innegables. Però abans usàvem la ploma i ara escrivim per ordinador. En aquest camí la ciència ha realitzat ja més d'un exercici d'humilitat: ha hagut d'acceptar la teoria de la relativitat, sovint hem començat a tenir en compte la influència implícita del propi mesurament en el fenomen que es quantifica; els mètodes d'aproximació s'han convertit en imprescindibles; els agents que es consideraven poc importants, els que descartàvem amb facilitat, hem hagut de tornar a recordar i mesurar el seu efecte. Igual ocorre en el cas que ens ocupa i els anunciants no encerten perquè descarten l'efecte del vol de la papallona. Si en els seus càlculs també incloguessin aquest factor, les prediccions podrien ser més segures.
Cada vegada millors mesuraments sense parar?
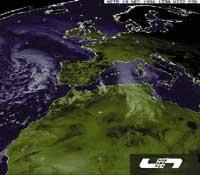
Avui dia, els satèl·lits recullen dades recollides en milers d'observatoris meteorològics repartits per tot el món: la pressió atmosfèrica, la temperatura i molts altres paràmetres es recullen periòdicament en els observatoris de tota la Terra, així com fotografies espectaculars. Es creu que quant millors siguin els aparells de mesura, més precisos es faran. Però això no té límits?
Suposem que tenim tots els mesuradors que vulguis distribuïts per tot el món. Cal tenir en compte que aquests mesuradors són capaços de detectar cada part de l'aire d'Euskal Herria des de l'aire que envolta a la papallona del Carib. Segons la teoria cinètic-molecular bàsica que interpreta les propietats dels gasos, els xocs moleculars provoquen la pressió i la temperatura de l'aire.
Aquestes últimes afecten directament el moviment de l'aire. Si en un moment donat coneixem la posició de cadascuna de les molècules que componen l'aire, podem saber on estaran en el següent moment? Si fóssim capaços de detectar cada xoc, podríem predir la següent posició. Però si els detectors són tan petits com vulguem, ens donen la direcció i posició de cada molècula, segurament necessitarem molts aparells per a omplir l'espai que ocupa l'aire en tota l'atmosfera.
No obstant això, i malgrat donar a cadascun dels habitants del món el seu escafandre d'oxigen, per a poder mesurar cada impacte, els mesuradors modificaran en un moment o un altre el moviment previst i la previsió realitzada es cancel·larà i el mesurament total haurà de començar per zero. Sembla que tampoc avançarem en aquest aspecte.
Teoria de la Relativitat
De totes maneres, avançarem sense desesperar-nos i pensar que inventem un model informàtic global. L'ordinador processa totes les dades que vulguis. També la velocitat de càlcul perquè puguem accelerar el que vulguem. No obstant això, lamentablement o afortunadament, haurem d'acceptar una limitació: Segons la teoria de la relativitat d'Einstein, el nostre univers té la màxima velocitat, la velocitat de la llum, és a dir, la màxima velocitat en la naturalesa.
És un número d'un munt de zeros, sí, però limitat. Introduirem les dades a aquesta velocitat: tres-cents milions de dades per segon. Per a poder fer un pronòstic d'una setmana, quantes dades concretes hauríem d'introduir? En condicions normals, és a dir, a una temperatura de 25 °C i una pressió d'1 atm, es pot dir que en un litre d'aire hi ha aproximadament 3 x 1.022 molècules, és a dir, introduint tres-cents milions de dades per segon, necessitarem gairebé dos minuts per a introduir dades d'un litre. En una setmana hi ha 10.080 minuts, per la qual cosa podrem introduir les dades corresponents a 5.040 litres. Sense grans càlculs, qualsevol sap que en la nostra atmosfera hi ha molt més litres d'aire que això.
Per tant, malgrat estar tan desenvolupats com vulguem, difícilment introduirem en l'ordinador a temps aquesta enorme quantitat de dades que necessitem. Volem fer un pronòstic per a una setmana i passar una setmana introduint una petita part de les dades! Per tant, no és necessari anar més enllà. No podrem tenir en compte totes les dades, hem de descartar alguns i, juntament amb el rebuig, perdre precisió.
Estadística
Analitzem la qüestió d'una altra manera; quan parlem del temps, moltes vegades escoltem la paraula front. Ens està acostant un front fred, però abans el front càlid travessarà el territori... Aquests fronts són conjunts d'aire o, més concretament, límits entre diversos grups d'aire. No parlem de molècules, sinó de les “parts” de l'aire i els seus límits. Podem conèixer totalment les “parts” de l'aire? En cas afirmatiu, el nostre problema estaria resolt: una vegada conegudes les parts, estaríem completament determinades, per la qual cosa podríem predir el temps futur. Podem pensar que l'efecte que ha produït la nostra papallona en assotar les ales ens acostés en algun front, aquest dia, sense que es produeixi cap desconeixement especial. Però com determinar cada part sense tenir en compte els seus components?

La conceptualització estadística en ciència és molt útil: quan el comportament de cadascun dels components d'un succés és inexacte, utilitzem l'estadística aplicada. En el nostre cas, no seria necessari analitzar els xocs de les molècules dels components de l'aire de manera separada, sinó que cada grup d'aire es trobaria estadísticament parlant, utilitzant paràmetres com la freqüència d'intercalació-triple-impacte en una direcció intermèdia. Però, en definitiva, hauríem d'utilitzar una probabilitat tan lligada a l'estadística: podríem parlar del temps més probable per a la setmana que ve, i tots sabem perfectament en quin percentatge no es compleix el més probable.
Per tant, no sembla que d'aquesta manera les coses vagin amb la precisió que volem. A més, ja saps el que diu el vell lector: “jo hem menjat dos txangurros i tu cap, una mitjana segons l'estadística”. A on anem amb això a buscar el nostre detall? En qualsevol cas, és cert que quants més dades tinguem podrem fer prediccions més concretes. I un pot pensar que a mesura que la ciència avança, la majoria de les prediccions estarem en condicions d'inventar-se durant una setmana. Així sigui, però gairebé segur que arribem als mesos i ens preguntarem: “per què els anunciants fallen tant?”
El vol de la papallona pot provocar una tempesta de vent. No tenim en compte el petit vol, o ens resulta totalment impossible tenir-lo en compte, i vivim bé a pesar que la setmana que ve no sabem el temps que tindrem. Cal conformar-se amb el que deia aquell ministre: el més probable és que no sabem.





