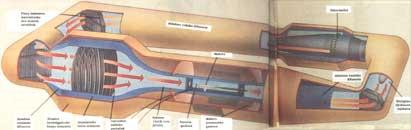
Tunnels cryogéniques
Problèmes de l'échelle
Pour comprendre l'influence du changement de taille tout en gardant la même forme, nous allons mettre quelques exemples. Quand le coléoptère tombe de la pointe de l'arbre, il ne subit aucun dommage à son arrivée au sol. Bien que le chat ne tombe pas, mais pour une autre raison. Il ne s'agit pas que le corps de l'un soit plus élastique que l'autre, mais qu'il ait une grande résistance à l'air et une faible vitesse à l'arrivée au sol. C'est ce qui arrive au coléoptère. Mais au chat non.
Les deux ont le même air, mais le chat est plus lourd que sa surface. Le chat tombera comme une pierre environ, et si vous n'avez pas de blessures, c'est parce qu'il a un sentiment d'équilibre surprenant et une capacité incroyable.
Même lorsque des maquettes d'avions sont testées, la résistance à l'air génère de nombreux problèmes. Prenons comme exemple la maquette d'un modèle d'avion. Si nous faisons une maquette deux fois plus longue, la surface en contact avec l'air est quatre fois plus grande et le poids huit fois plus grande. Cependant, la vitesse de chute dans l'air dépend de la surface et du poids et, comme déjà indiqué, ces deux facteurs ne varient pas dans la maquette dans la même proportion. Les données obtenues avec une petite maquette ne peuvent donc pas être extraites au modèle réel et inversé.
Dans les tunnels aérodynamiques, il ne s'agit pas d'étudier la chute de l'avion, mais de son vol, c'est-à-dire la résistance de la maquette à la vitesse à laquelle l'avion réel doit circuler. Cependant, l'exemple donné montre clairement que l'utilisation de données de bas modèle en aéronautique pour de grands appareils réels a ses difficultés.

L'air n'est pas un fluide continu sans matière, mais un gaz de millions de molécules comme les dunes de sable. Dans le cas du sable, nous savons que la taille du grain et la taille du véhicule sur lequel vous circulez ont un rapport. La pelle à pneus larges circulera facilement dans le sable, car il est un matériau continu par rapport à la taille des roues. La petite maquette de cette même pelle, cependant, serait très mal dans les sables en raison de l'accumulation de grains de sable autour de la roue. Si le sable est conflictuel, le problème devient encore plus compliqué.
Il faut noter, cependant, que les molécules d’air sont “conflictuelles” et que les gouttes de pluie s’attachent à n’importe quelle surface comme au verre de la fenêtre.
Pour réafficher le problème de l'échelle, nous dirons que le phénomène de collage est proportionnel à la taille du verre. Pour couvrir tout le verre qui précède la voiture de jouet, par exemple, il suffit d'une goutte de pluie, tant qu'aucun obstacle ne se produit pour la voiture réelle.
Numéro de Reynolds
Mais nous venons au cas de l'avion qui doit déplacer les molécules confrontées. Les effets ne seront pas exclusivement proportionnels aux mesures des ailes. Dans ce problème d'échelle le nombre de Reynolds a une grande importance, puisque moins de 2.000 le régime est laminaire et au-delà turbulent. Pendant le vol de l'avion, la pression exercée sur la surface des ailes exerce une force d'entretien sur l'air et oppose la résistance à l'air pour avancer. Cependant, sous pression superficielle, le régime de la fine couche d'air en contact avec les ailes a beaucoup à voir.
Lorsque le régime est laminaire, on applique la force de maintenir l'avion dans l'air en collant le calque au sud. Si le régime est turbulent, cette couche d'air commence à turbuler et s'éloigne de la surface. L'avion s'oppose plus à l'air et dépense plus avec des brûlures. En outre, si de nombreuses tourbillons se produisent sur les pentes, l'avion peut tomber.
Sur des ailes de même forme et de taille différente (l'une véritable et l'autre est une maquette), sa résistance à l'air à la même vitesse et sa force d'entretien dans l'air ne sont pas proportionnelles aux dimensions. C'est pourquoi en aérodynamique il est fondamental de savoir réaliser des spectres aérodynamiques sur des maquettes de la même forme géométrique et de taille différente (le spectre est l'ensemble de lignes qui marquent la trajectoire du fluide autour du solide).
XIX. Au XIXe siècle, l'anglais Osborn Reynolds a enquêté sur les grandeurs qui interviennent dans le passage du régime laminaire au turbulent, donnant une solution au problème de l'échelle quand il a publié sa loi de ressemblance. La loi stipule que les spectres aérodynamiques de deux corps similaires orientés de façon similaire sont similaires lorsque la relation entre la résistance aux villosités et la résistance au frottement laminaire est la même. La présente loi de similitude est formulée avec la formule suivante: .v.d/e = R = constante ( R est le nombre de Reynolds, la longueur correspondant à la taille du corps d, la vitesse de déplacement du corps v, la masse spécifique du fluide et la viscosité du fluide e).

Pour revenir à notre exemple, l'avion réel et sa maquette doivent avoir le même numéro que Reynolds pour que les données soient extrapolables. La dimension d m de la maquette est, logiquement, beaucoup moins que le d h de l'avion réel, et aussi le nombre de Reynolds de la maquette.
Dans Aérodynamique on connaît depuis longtemps les facteurs correcteurs pour le passage de données de mineur à majeur modèle, mais ils ne sont pas très précis et l'erreur de 2 ou 3% ne peut pas être écartée pour le moment. Cela signifie que l'avion circulera plus lentement et brûlera plus.
Cependant, comme nous venons de le voir, si le nombre de Reinolds diminue d pour rester égal, il faut augmenter r ou diminuer e (nous ne changerons pas la vitesse parce que chaque avion a une vitesse d'essai déterminée).
L'agrandissement r consiste en une plus grande pression d'air dans le tunnel aérodynamique. Pour cela, il faut un éventail plus puissant et les coûts augmentent.
Un autre des paramètres que nous avons encore pour augmenter le nombre de Reynolds et que les résultats de la simulation soient réels est le changement de viscosité de l'air du tunnel. Si dans la formule de Reynolds diminue e e, R augmente et pour réduire la viscosité de l'air on refroidit l'air jusqu'à -173 ºC (jusqu'à 100 kelvin) en tunnels cryogéniques. Aux Etats-Unis, le centre de recherche d'ADN à Langley a prouvé que la viscosité du gaz de circulation en abaissant la température à 100 K est six fois inférieure. Donc, le nombre de Reynolds est six fois plus élevé. En agissant avec la pression et la température de l'air, on obtient de maintenir le nombre de Reynolds le moins cher possible.
Tunnel cryogénique allemand
Le premier tunnel aérodynamique cryogénique d'Europe est le KKK (Kryo-Canal Köln), qui peut atteindre le nombre de Reynolds de 9 millions. Il est situé près de Cologne dans le centre de recherche aérospatiale DLR. Ce tunnel de test à faible vitesse (jusqu'à 400 km/h) a beaucoup changé pour travailler à des températures très basses.
Entre autres choses, une nouvelle isolation thermique et un système d'injection d'azote liquide ont été appliqués avec le système de contrôle.
Pour atteindre des températures de 100 K (-173 °C), l'azote liquide est utilisé de 65 à 90 tonnes. En quatre heures il refroidit 50K par heure et puis en vingt heures 10K par heure. 100 K Entretien en 24 heures nécessite 58 tonnes supplémentaires d'azote liquide. Son éventail est d'un mégawatt et son coût d'exploitation est de 1.700.000 pesetas par jour.
Tunnel cryogénique des États-Unis
La NASA à Langley sera probablement le plus grand tunnel cryogénique au monde. Il a été construit dans l'ancien tunnel aérodynamique, qui a coûté environ 10 milliards de pesetas. Son éventail est de 90 mégawatts anciens, avec une capacité de neuf atmosphères de pression. Il atteint des températures allant jusqu'à 124 K (-149 °C) et des vitesses de 1,2 mâles.

Le nombre de Reynolds que l'on peut obtenir est de 100 millions (il a vraiment été obtenu dans un essai effectué à une vitesse de 1,0 mâles), le plus grand obtenu dans aucune installation terrestre.
Le refroidissement de l'air est obtenu en quatre heures en utilisant 70 tonnes d'azote liquide. Depuis sa première en 1984, des essais de maquettes ont été réalisés comme celle de Boeing 757 et d'autres avions militaires. L'ADN l'utilise également pour tester des maquettes de ses espaces.
Tunnel cryogénique européen
Comme le tunnel allemand ne comprime pas l'air, on construit à côté de l'autre un tunnel appelé ETW (European Transonic Windtunel). La France, l'Allemagne, la Grande-Bretagne et la Hollande se sont unies pour financer ce projet. Il faudra un certain nombre de Reynolds de 50 millions à 0,9 mâles. Les températures vont de 90 à 120 K (-150 à -183) et la pression maximale est de 4,5 bars. Le ventilateur peut atteindre des vitesses de 1,3 mâles avec sa puissance de 50 mégawatts. Dans ce tunnel, on veut tester, entre autres, les modèles de l’avion «Airbus».
Tester les maquettes des avions dans des tunnels aérodynamiques est une technique coûteuse, mais il semble qu'ils seront encore utilisés depuis longtemps. L'informatique a beaucoup avancé et des simulations peuvent être effectuées sur les ordinateurs. Cependant, ces simulations sont réalisées en deux dimensions et non dans trois conditions critiques. En outre, on a pu constater qu'ils sont chers. Le tunnel aérodynamique cryogénique a donc un avenir.





