Cryogenic tunnels
Problems of the scale
To realize the influence of the size change keeping the same way, let's put some examples. When the beetle falls from the tip of the tree, on reaching the ground it does not suffer any damage. Although the cat does not fall, but for another reason. It's not that one's body is more elastic than the other, but that it has a great resistance to the air and a low speed when reaching the ground. That's what happens to the beetle. But to the cat no.
Both have the same air, but the cat is heavier than its surface. The cat will fall like a stone approximately, and if it has no wounds it is because it has a surprising sense of balance and an incredible ability.
Even when aircraft models are tested, air resistance generates many problems. Take as an example the model of an aircraft model. If we make a model twice longer, the surface in contact with the air is four times larger and the weight is eight times larger. However, the speed of falling in the air depends on the surface and the weight and, as has already been indicated, these two factors do not vary in the model in the same proportion. The data obtained with a small model cannot, therefore, be extrapolated to the real model and the reverse.
In the aerodynamic tunnels it is not a question of studying the fall of the plane, but of its flight, that is, the resistance of the model to the speed at which the real plane must travel. However, the given example clearly demonstrates that the use of low model data in aeronautics for large real devices has its difficulties.

The air is not a continuous fluid without matter, but a gas of millions of molecules like sand dunes. In the case of sand, we know that the size of the grain and the size of the vehicle on which it will circulate are related. The wide tire excavator will easily circulate through the sand, as it is a continuous material compared to the size of the wheels. The small model of this same excavator, however, would be very bad in the sands due to the accumulation of sand grains around the wheel. If the sand is conflicting, the problem is further complicated.
It must be taken into account, however, that the air molecules are “conflicting” and that the raindrops stick to any surface like the window glass.
To show again the problem of the scale, we will say that the gluing phenomenon is proportional to the size of the glass. To cover all the glass that precedes the toy car, for example, just a drop of rain, while there is no obstacle to the real car.
Number of Reynolds
But we come to the case of the plane that has to displace the opposing molecules. The effects will not be exclusively proportional to the measures of the wings. In this problem of scale the number of Reynolds has great importance, since less than 2,000 the regime is laminar and beyond turbulent. During the flight of the plane, the pressure exerted on the surface of the wings exerts a maintenance force on the air and counteracts the air resistance to advance. However, at surface pressure, the regime of the thin layer of air in contact with the wings has much to do with.
When the regime is laminar, the force of keeping the plane in the air is applied by gluing the layer to the south. If the regime is turbulent, this layer of air begins to turbular and moves away from the surface. The plane opposes more on the air and spends more with burns. Also, if on the hillsides there are many trailers, the plane can fall.
In wings of equal shape and of different size (one true and the other is a model), its air resistance at the same speed and its maintenance force in the air are not proportional to the dimensions. Therefore, in aerodynamics it is essential to know how to perform aerodynamic spectra in models of the same geometric form and of different size (the spectrum is the set of lines that mark the trajectory of the fluid around the solid one).
XIX. In the nineteenth century the English Osborn Reynolds investigated the magnitudes that intervene in the passage of the laminar regime to the turbulent, giving solution to the problem of the scale when he published his law of resemblance. The law establishes that aerodynamic spectra of two similar bodies similarly oriented are similar when the relationship between the resistance to villi and the resistance to laminar friction is the same. The present law of similarity is formulated with the following formula: .v.d/e = R = constant ( R is the number of Reynolds, the length corresponding to the size of the body d, the speed of displacement of the body v, the specific mass of the fluid and the viscosity of the fluid e).

Returning to our example, the real plane and its model must have the same number as Reynolds to make the data extrapolable. The dimension d m of the model is, logically, much smaller than the d h of the real plane, and also the number of Reynolds of the model.
Aerodynamics has long known the corrective factors for the passage of data from minor to major pattern, but they are not very precise and the error of 2 or 3% cannot be ruled out at the moment. This means that the plane will circulate slower and burn more.
However, as we have just seen, if the number of Reinolds decreases d to remain the same, we must increase r or decrease e (we will not change the speed because each plane is applied a certain test speed).
The expansion r consists of a higher air pressure in the aerodynamic tunnel. For this, a more powerful fan is needed and costs increase.
Another of the parameters we still have to increase the number of Reynolds and that the results of the simulation are real is the viscosity change of the tunnel air. If in the formula of Reynolds decreases e, R increases and to reduce the viscosity of the air cools the air up to -173 °C (up to 100 kelvin) in cryogenic tunnels. In the United States, the DNA research center in Langley has shown that the viscosity of the circulation gas by lowering the temperature to 100 K is six times lower. So the number of Reynolds is six times higher. Acting with pressure and air temperature, it is possible to keep the number of Reynolds as cheap as possible.
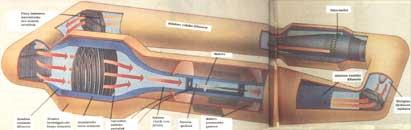
German cryogenic tunnel
The first cryogenic aerodynamic tunnel in Europe is called KKK (Kryo-Canal Köln), which can reach the number of Reynolds of 9 million. It is located near Cologne in the DLR aerospace research center. This tunnel for low speed tests (up to 400 km/h) has changed a lot to work at very low temperatures.
Among other things, a new thermal insulation and a liquid nitrogen injection system has been applied together with the control system.
Liquid nitrogen from 65 to 90 tons is used to reach temperatures of 100 K (-173 °C). In four hours it cools 50K per hour and then in twenty hours 10K per hour. 100 K Maintenance in 24 hours requires 58 additional tons of liquid nitrogen. Its fan is a megawatt and its operating cost is located at 1.700.000 pesetas per day.
Cryogenic tunnel of the United States
NASA's in Langley will probably be the largest cryogenic tunnel in the world. It has been built in the old aerodynamic tunnel, which has cost about 10,000 million pesetas. Its fan is 90 megawatts old, with a capacity of nine atmospheres of pressure. It reaches temperatures up to 124 K (-149 °C) and speeds of 1.2 males.

The number of Reynolds that can be obtained is 100 million (it has actually been obtained in a trial at a speed of 1.0 males), the largest obtained in any terrestrial installation.
Air cooling is achieved in four hours using 70 tons of liquid nitrogen. Since its premiere in 1984, models such as Boeing 757 and other military aircraft have been tested. DNA also uses it to test models of its spaces.
European cryogenic tunnel
As the German tunnel does not compress air, a tunnel called ETW (European Transonic Windtunel) is being built next to the other. France, Germany, Britain and the Netherlands have joined forces to fund this project. It will carry a number of Reynolds from 50 million to 0.9 males. Temperatures range from 90 to 120 K (-150 to -183) and maximum pressure will be 4.5 bars. The fan can reach speeds of 1.3 males with its power of 50 megawatts. In this tunnel we want to test, among others, the models of the plane “Airbus”.
Testing aircraft models in aerodynamic tunnels is an expensive technique, but it seems that they will still be used for a long time. Computer science has advanced a lot and simulations can be performed on computers. However, these simulations are performed in two dimensions and not in three and critical conditions. In addition, it has been possible to verify that they are expensive. The cryogenic aerodynamic tunnel therefore has a future.





