Tangram
Ja hem portat els puzles o “capgrossos” i alguns jocs xinesos, les dames i els escacs. En aquesta ocasió et portem a un “trencaclosques” xinès: El famós TANGRAM. I ho diem famós, segurament perquè ja ho coneixes. (Figura 1).

Comencem recordant la seva història.
XIX. En la introducció d'un llibre sobre els trencaclosques xinesos del segle XX es pot llegir que l'origen del tangram (i fins i tot l'inventor) era desconegut.
El nom xinès del Tangram és Ch’i Ch'ae pa (joc dels set elements). Chu alt (740-330 a. C.) La paraula és. El nom prové d'un costum xinès. I és que el setè dia del setè mes era feliç passar un fil pels set zuelos d'una agulla.
Els primers llibres publicats sobre el tangram apareixen en l'època de l'emperador Ch’ing Chia Ch’ing (1796-1820), el primer en 1813. No obstant això, el joc ja estava molt estès. A Europa, per exemple, sembla que el primer llibre va aparèixer en 1805.
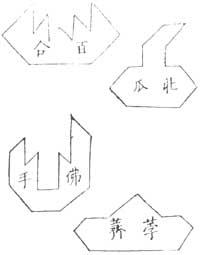
Els llibres xinesos es divideixen en dues parts. En la primera es plantegen problemes i en la segona es plantegen solucions. Els problemes porten un símbol xinès amb la intenció d'explicar el significat de la imatge, encara que aquesta és tan quadrada com abstracta (veure figura 2).
El joc suposaria un gran èxit, tal com indica el munt de llibres publicats des de 1813. Es va estendre ràpidament per Europa i Amèrica i per a 1818 ja es podien trobar llibres a Alemanya, Gran Bretanya, França, Itàlia i Àustria. En 1817 M. Es va publicar un article de Williams en el qual es presenten una sèrie d'exercicis matemàtics que poden resoldre's amb ajuda del tangram. El mateix Napoleó, durant el seu exili, va ser un gran amant del tangram.
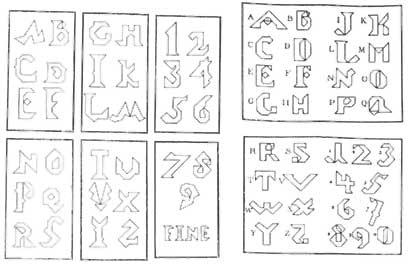
Els llibres europeus i americans eren principalment còpies de xinesos. No obstant això, van aportar al tangram, la lletra i xifra més àrab. Encara que hem dit una aportació, es van fer diferents versions d'aquestes lletres i xifres (veure figura 3).
Si al principi un dels atractius del joc era poder crear noves imatges, a poc a poc aquest avantatge es va anar perdent (però encara no ha acabat del tot).
Tangram no és un joc de competició, sinó individual.
El joc està format per set peces llises, com dos triangles petits (iguals), un triangle, un quadrat i un romboide (cadascun pot estar format per dos triangles petits anteriors) i dos triangles grans (que poden estar formats per quatre triangles petits) (veure figura 1). Aquest joc no té regles. No obstant això, té dos límits o regles:
- Totes les imatges han de completar-se amb set peces.
- Totes les imatges són launas (no es poden fer piràmides).

Respectant aquestes dues condicions, el jugador podrà fer el que desitgi amb les fitxes (per exemple, el romboide pot ser utilitzat per totes dues cares).

Convexes Tangram
Amb les peces del Tangram es poden formar infinites imatges. N'hi ha prou amb moure una mica una peça en una imatge. Però donem una mica de serietat o rigor al joc.
Com es pot apreciar, totes les peces del joc són convexes. La pregunta ara és: Quantes imatges convexes es poden construir amb el tangram? Aquesta vegada la resposta no és infinita, no. En 1942 Fu Traing Wang i Chuan Chih Hsiung van demostrar que aquestes imatges convexes tindran un màxim de vuit costats. Després, tenint en compte que les imatges convexes s'emmarquen dins d'un rectangle, també es va demostrar que es creaven 20 imatges convexes.
Només 13 d'elles es poden construir amb peces del tangram (veure figura 5). En aquestes proves van suposar que aquestes imatges convexes havien de construir-se utilitzant 16 triangles com els petits triangles, ja que el tangram es pot dividir en 16 triangles petits.

Tangram divisibles
Amb aquest nom, si es divideixen les peces del tangram en dos grups, es tracta de nomenar els que s'obtenen formant les mateixes figures amb les peces de cada grup (veure figura 6).

Per a acabar direm que no falten altres jocs “tangram” que s'assemblen al tangram xinès. A continuació es mostra aquest ou i algunes imatges que es poden completar amb les seves peces. (Veure figura 7).
Encara que podríem dir més coses, creiem que el millor per a entendre bé el tangram és jugar. Aquí tens una petita mostra de les possibilitats que ofereix el joc. (Veure figura 8). Intenta-ho!








