Cambio de base
Coa escusa de que estabamos no último número no verán, ofrecémosvos un xogo. Por suposto que logo xogariades o suficiente e ao final do verán temos que volver á vía. Estamos ao principio dun novo curso e é hora de empezar a pór en marcha os motores. Esperamos que o programa deste número axúdevos neste traballo.
O sistema normal utilizado paira representar os números é o harmático, é dicir, un sistema formado por dez signos ou díxitos diferentes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). De todos os xeitos, saberedes que os computadores traballan no sistema binario, é dicir, no sistema de 0 e 1 díxitos, polo que paira poder procesar os datos introducidos por nós ten que pasar dunha base a outra e o mesmo, pero viceversa, paira presentar ao usuario os resultados obtidos.
O que quixemos analizar neste programa foi: os cambios de base.
Tomamos como exemplo as bases 10, 2 e 16, que son as que máis se utilizan ao noso xuízo.
Conversión de base 10 a base n
Supoñamos que queremos converter á base n un número que está na base 10. Dividimos o número decimal por n e gardamos os restos destas divisións ata que o cociente é 0.
Ex. : Si queremos converter o número decimal 408 á base 2:
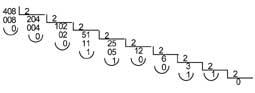
O número 408 na base 2 será 110011000.
Ex. : Conversión do número decimal 420 á base 16
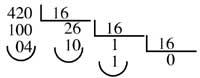
1A4 será o número 420 na base 16.
Nota: O sistema decimal utiliza 10 díxitos e o binario 2. Por tanto, o hexadecimal deberá ter 16 díxitos ou símbolos. Como só hai 10 cifras decimais, utilízanse os 6 primeiros caracteres do alfabeto como cifras.

Conversión de base n a base 10
Supoñamos que queremos pasar un número na base n (a1 a2 ... á base 10.
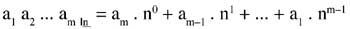
Temos que facelo.

Non se pode facer directamente paira converter o número m-tar en n-tar sen pasar pola base 10. O número m deberá converterse en decimal e despois en n-tar o decimal.
Con todo, paira converter os números binarios en hexadecimales temos una ruta máis sinxela que paira o caso xeral. Por que isto? Pois porque o catro díxitos binarios forman un número hexadecimal. Por tanto, coller os díxitos binarios de dereita a esquerda, si no grupo da esquerda falta cifra engadindo os 0 á esquerda, e seguindo a táboa adxunta bastará con converter directamente a dezaseis.

Partes do programa:
- 10-130: Presentación do menú principal e selección dunha opción.
- 140-200: Definir o número de exercicios que se queren realizar nunha sesión.
- 250-550: Resolución dun conxunto de exercicios.
- 270: Un número decimal extráese aleatoriamente.
- 290-330: O número decimal pasa á base 2.
- 340-400: O número decimal pasa á base 16.
- 410-430: Defínese a base na que deben estar presentes as preguntas ou entradas e os resultados.
- 450-530: Verificación do resultado.
- 610-640: Acción de escribir lentamente as cadeas de caracteres cara á dereita.
- 660-690: Acción de escribir as cadeas de caracteres cara á esquerda.
- 710-730: Datos do programa.






