Mezclado IV
Parece que cuando nos acercamos a unas vacaciones la publicación de una nueva colección de desórdenes se está convirtiendo en una costumbre. Esa es nuestra intención. A lo largo del año abordaremos temas más serios (como hasta ahora) y en el número de julio-agosto, con el objetivo de relajar la mente o lanzar una colección como ésta. Mientras no recibamos ninguna opinión en contra, lo haremos así. Respecto al grano de diciembre, sin embargo, estamos en mi poder. En esta época también tenemos días libres. Sin embargo, tenemos la duda de que sacar dos colecciones de este tipo en el mismo año no es demasiado. ¿Qué opinas?
Por otro lado, todos sabemos cosas como las que aparecen aquí, juegos, rayas… Queremos proponernos que nos envíes tus conocimientos y tu nombre y te prometemos que los publicaremos completamente.
Las respuestas a las preguntas que se plantean en el siguiente número, es decir, en el número 63. Y para terminar, este apartado quiere ser un lugar de intercambio de lectores, pero para ello necesitamos tu colaboración. ¡Anímate!.
1. El de Zirano Bergerac lo planteó en su viaje a la luna. Sabemos que cuando tiramos de los extremos de una cuerda se rompe del punto más débil. Supongamos que tenemos una cuerda con todos sus puntos iguales, es decir, con sección constante. Tiremos de los extremos, ¿lo cortamos? Si es así, ¿dónde se detendrá? Recuerda que no tiene puntos más débiles que los demás. ¿Se suspenderá en todos los puntos?
2. Soy capicua, tengo un único divisor entre 2 y 10, tengo cuatro cifras, hay quien me ve como 9. ¿Qué número soy?.
3. ¿Cuál de estas dos secuencias no es adecuada?
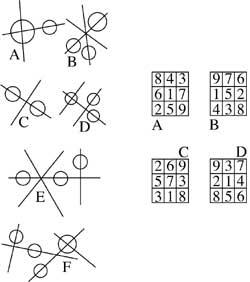
4º En una tabla de damas hay que colocar 13 fichas para que una dama contraria las coma en una única jugada. Si ha sido fácil, esta vez el movimiento de la dama comienza y termina en el mismo recuadro.
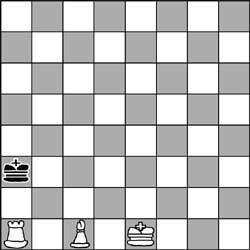
5. Aunque parezca mentira, tanto la torre como el perfil están dando ajedrez al rey. La posición de esta partida de ajedrez es correcta. ¿Cuál ha sido el último movimiento de los blancos?.
6º ¿Por qué es más fácil apagar una vela soplando que aspirando? (en ambos casos con la misma fuerza).
7. A cada lado de una balanza hay un balde lleno de agua y un peso, con la balanza equilibrada. Si metes un dedo al agua, sin tocar el balde, ¿se mantendrá el equilibrio?
8º. ¿Cuál es el mayor número de distritos que pueden estar limitados por cinco rectas? ¿Y las cuatro circunferencias?.
9. ¿Se pueden colocar 14 alfiles en la tabla de ajedrez sin agredir?
10. La imagen lateral está formada por 8 piezas de igual forma y tamaño. ¿Cómo son las piezas y cómo están colocadas?

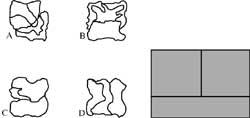
11. Uno de estos mapas puede convertirse en una imagen de la derecha. ¿Cuál es?.
12. Un artesano quiere aserrar un cubo para conseguir 27 cubitos iguales. Cada corte es correcto, pudiendo acumular las partes cortadas. ¿Cuál es el menor número de cortes?.
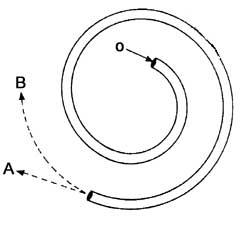
13. ¿Qué dirección se seguirá cuando la bola salga del tubo?
14. ¿Qué mide 23 pulgadas en un televisor de 23 pulgadas?
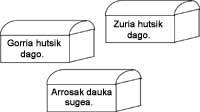
15. Una de estas cajas tiene un tesoro, otra una serpiente y la tercera está vacía. Sabiendo que sólo la etiqueta de la caja con el tesoro es cierta, ¿en qué caja está el tesoro?.
16. En esta tabla de ajedrez las letras J, K, L, M y N son el rey, la dama, la torre, el alfila y el caballo (no en este orden). Los números que aparecen en varias casillas indican el número de piezas que atacan la casilla. Adivina qué pieza es cada letra.

17. El número 43 es especial, ya que cumple 43 = 42 + 33. Hay un único número de dos cifras con la misma propiedad (el número es el cuadrado de la primera cifra y la suma del cubo de la segunda). ¿Cuál es?.
18. ¿Cuál es el camino más corto del rey negro para llegar al otro vértice negro de la tabla?. El rey se mueve solo, puede comer las piezas que desee, pero no se puede meter el ajedrez.

19. Los números 17 y 18 tienen una propiedad especial:
173 = 4913 y 4 + 9 + 1 + 3 = 17183 = 5832 y 5 + 8 + 3 + 2 = 18
Muy cerca hay otros dos números con la misma propiedad. ¿Cuáles son?.
20. En el pueblo tienen un curioso sistema monetario. Tienen dos monedas de valor: 10 y 7. Nuestra pregunta también es curiosa. Sin embargo, tiene una solución sencilla: ¿cuál es la mayor cantidad que no se puede pagar exactamente con estas monedas?.
21. Los números 100 y 164 tienen una característica común, es decir, sumando 125 a los dos se obtienen 225 y 289, que son los antiguos cuadrados de los números 15 y 17. ¿Qué otro número se puede añadir a los números 100 y 164 para obtener otros dos cuadrados concretos?.
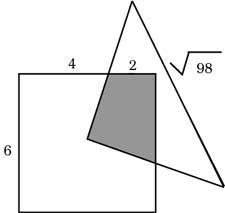
22. En la imagen se sitúa el vértice del triángulo isósceles en el centro del cuadrado. ¿Cuál es la superficie trazada?.
23. En un restaurante un amigo encontró una mosca en su café. Llamó al servidor y le pidió que traiga otro. Nada más beber un chorro, gritó “¡Esta taza es la misma!”. ¿Cómo se dio cuenta?.
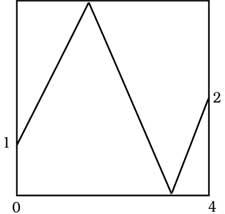
24. En la imagen una pelota parte del punto de coordenadas (0,1) y finaliza el recorrido en el punto (4,2). En qué punto sonará en las partes superior e inferior.
25. En el juego de dominó sabemos cómo unir las fichas. Por ejemplo, las fichas 2-3 y 3-4 se unen mediante 3. En esta ocasión queremos coger dos fichas de dominó para juntarnos. ¿De cuántas formas diferentes podemos conseguir?.
26. Completa con todas las cifras del 1 al 9 la diferencia entre dos números de nueve cifras (sin repetir cifras) para obtener un número formado por nueve cifras diferentes.
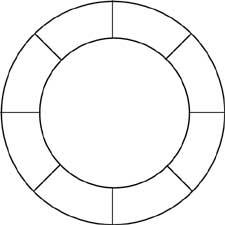
27. Coloca en la rueda lateral los números del 1 al 8 de la siguiente manera: suma de las siguientes de 4, suma de las siguientes de 9, 5, suma de las siguientes de 11, 6, para que la suma de 10 y 7 sean 8.
28. ¿Sabes cuál es el último número de esta serie? : 2, 2, 6, 5, 8, 8, 4, ? ...
29. Dos parejas juegan un partido en las cartas. Se reparten 40 cartas cada 10. ¿Qué es más fácil, que a una pareja le toquen todos los oro o que no le toque un oro?
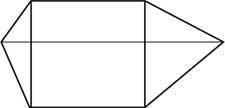
30. Construir una pirámide con dos piezas como la de la imagen.
31. Tomemos el número 8476 y hagamos el siguiente proceso:
8.4.7.6 = 1344; 1.3.4.4 = 48;4.8 = 32; 3.2 = 6
Mediante este proceso, descubre los dos números consecutivos más pequeños que dan el mismo resultado (6 u otro). Similar pero ahora los tres números pequeños consecutivos.
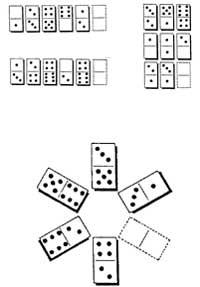
32. Cuáles son las fichas que faltan en los siguientes pasos:
33. Tenemos un cuadrado y queremos dividirlo en triángulos agudos. ¿Sabes cómo? Y para dividirnos en triángulos desafíos, ¿qué deberíamos hacer?.

34. A través de cuatro rectas, sin levantar el lápiz, representadas una tras otra. Los 9 puntos de la imagen Bildu (se considerará que los puntos son adimensionales).

35. ¿Qué ves en la imagen?. ¡No cedas tan rápido!, porque lo has visto muchas veces.

36. Juego de globos:
- Coge, pero sólo doce —dijo Nagore mostrando las canicas de la caja—. Tenemos menos verde que el azul y menos azul que el rojo. Por lo tanto, que cada uno tome el mayor número posible de rojos y de verdes.
- Todos hemos sacado combinaciones diferentes —dijo Ainhoa—. Yo soy el único que ha sacado cuatro canicas azules.
- ¿Y? —Hasier recibió una de las canicas verdes que le cayó—. Vamos a jugar. En total había 26 canicas rojas. ¿Cuántos niños había?.
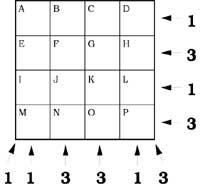
37º Se colocarán fichas en la tabla anexa. Los números que aparecen en los lados indican el número de fichas en filas, columnas o diagonales.
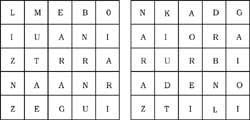
38º Encuentra 14 pueblos vascos (izquierda) y 10 ríos (derecha). Las letras de los nombres deben estar juntas, por vértices o por partes.
39. En el producto contiguo todos los asteriscos son los primeros números, pero ¿qué?.

40. A lo largo de la carretera se suceden cuatro pueblos. Los rojos viven junto a los verdes, pero no junto a los blancos, los azules no viven junto a los blancos. ¿Cuáles son los barrios de los blancos? :
- Rojos
- Verdes
- Rojos y verdes
- No se sabe





