Mixed IV
It seems that when we approach a holiday the publication of a new collection of disorders is becoming a custom. That is our intention. Throughout the year we will address more serious issues (as so far) and in the July-August issue, with the aim of relaxing the mind or launching a collection like this. As long as we do not receive any opinion against it, we will do so. Regarding the December grain, however, we are in my power. At this time we also have days off. However, we have the doubt that taking out two collections of this type in the same year is not too much. What do you think?
On the other hand, we all know things like the ones that appear here, games, stripes… We want to propose that you send us your knowledge and your name and we promise that we will publish them completely.
The answers to the questions posed in the following number, that is, in number 63. And finally, this section wants to be a place of exchange of readers, but for this we need your collaboration. Cheer up!.
1. The Zirano Bergerac posed on his trip to the moon. We know that when we pull the ends of a rope it breaks from the weakest point. Suppose we have a rope with all its equal points, that is, with constant section. We pull from the ends, do we cut it? If so, where will it stop? Remember that you have no weaker points than others. Will it be suspended at all points?
2. I am capicua, I have a single divisor between 2 and 10, I have four figures, there are those who see me as 9. What number am I?.
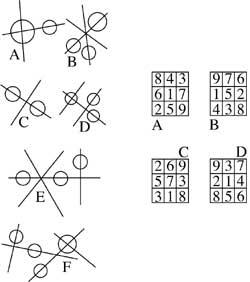
3. Which of these two sequences is not suitable?
4th In a checkers table you have to place 13 chips for a opposing lady to eat them in a single move. If it has been easy, this time the lady's movement starts and ends in the same box.
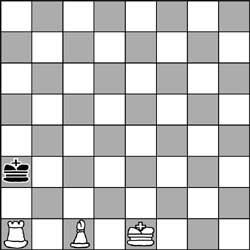
5. Even if it seems a lie, both the tower and the profile are giving chess to the king. The position of this chess game is correct. What has been the last white movement?
6. Why is it easier to turn off a candle by blowing than by sucking? (in both cases with the same force).
7. On each side of a balance there is a bucket full of water and a weight, with the balance balanced. If you put a finger into the water, without touching the bucket, will the balance remain?
8th. What is the highest number of districts that may be limited by five straight lines? And the four circles?.
9. Can 14 bishops be placed on the chess table without attacking?
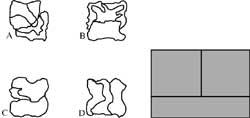
10. The side image consists of 8 pieces of equal shape and size. How are the pieces and how are they placed?

11. One of these maps can become an image on the right. What is it?.
12. An artisan wants to sawn a cube to get 27 equal cubes. Each cut is correct, being able to accumulate the cut parts. What is the least number of cuts?.
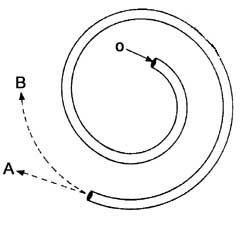
13. Which direction will follow when the ball leaves the tube?
14. What measures 23 inches on a 23-inch TV?
15. One of these boxes has a treasure, another a snake and the third is empty. Knowing that only the box label with the treasure is true, in what box is the treasure?
16. In this chess table the letters J, K, L, M and N are king, lady, tower, alfila and horse (not in this order). Numbers appearing in multiple boxes indicate the number of pieces attacking the box. Guess what piece each letter is.

17. The number 43 is special as it turns 43 = 42 + 33. There is a single number of two figures with the same property (the number is the square of the first figure and the sum of the cube of the second). What is it?.
18. What is the shortest way of the black king to reach the other black vertex of the table?. The king moves alone, you can eat the pieces you want, but you can't put chess in.

19. Numbers 17 and 18 have a special property:
173 = 4913 and 4 + 9 + 1 + 3 = 17183 =
5832 and 5 + 8 + 3 + 2 = 18
Nearby there are two other numbers with the same property. What are they?.
20. In the people they have a curious monetary system. They have two coins of value: 10 and 7. Our question is also curious. However, it has a simple solution: What is the largest amount that can not be paid exactly with these coins?.
21. Numbers 100 and 164 have a common characteristic, that is, adding 125 to the two are obtained 225 and 289, which are the old squares of numbers 15 and 17. What other number can be added to numbers 100 and 164 to get two more specific squares?
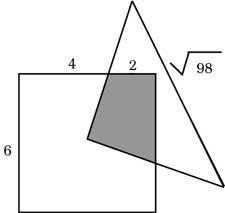
22. In the image is located the apex of the isosceles triangle in the center of the square. What is the surface drawn?.
23. In a restaurant a friend found a fly in his cafe. He called the server and asked him to bring another. “This cup is the same!” he shouted. How did you realize it?.
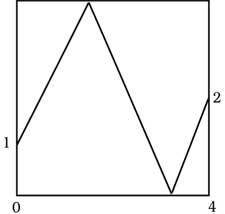
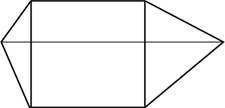
24. In the image a ball starts from the point of coordinates (0.1) and ends the route at the point (4.2). At what point it will sound at the top and bottom.
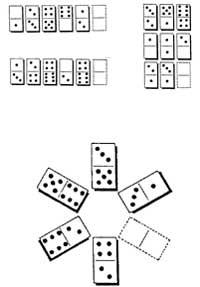
25. In the domino game we know how to join the tiles. For example, chips 2-3 and 3-4 are joined by 3. This time we want to take two dominoes to get together. How many different ways can we get?
26. Complete with all figures from 1 to 9 the difference between two numbers of nine figures (without repeating figures) to obtain a number consisting of nine different figures.
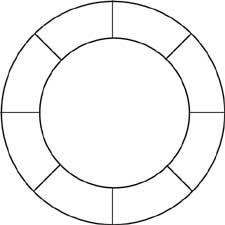
27. Place in the side wheel the numbers 1 to 8 as follows: sum of the following 4, sum of the following 9, 5, sum of the following 11, 6, so that the sum of 10 and 7 are 8.
28. Do you know what is the last issue of this series? 2, 2, 6, 5, 8, 8, 4, 4 ...
29. Two pairs play a match on the cards. 40 cards are dealt every 10. What's easier, if a couple gets all the gold or doesn't touch a gold?
30. Build a pyramid with two pieces like the image.
31. Take the number 8476 and do the following:
8.4.7.6 = 1344; 1.3.4.4 = 48; 4.8
= 32; 3.2 = 6
Through this process, discover the two smaller consecutive numbers that give the same result (6 or another). Similar but now the three consecutive small numbers.
32. What are the missing tiles in the following steps:
33. We have a square and we want to divide it into sharp triangles. Do you know how? And to divide ourselves into triangles challenges, what should we do?

34. Through four straight lines, without lifting the pencil, represented one after another. The 9 points in the Bildu image (points will be considered to be adimensional).

35. What do you see in the image?. Don't give up so fast, because you've seen it many times.

36. Balloon game:
- He grabs, but only twelve," Nagore said, showing the marbles in the box. We have less green than blue and less blue than red. Therefore, let everyone take as many reds and greens as possible.
- We have all drawn different combinations," Ainhoa said. I am the only one who has pulled out four blue marbles.
- What about? "Hasier received one of the green marbles that fell on him." Let's play. In total there were 26 red marbles. How many children were there?.
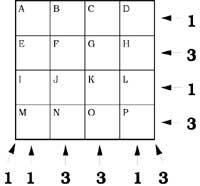
37º Chips will be placed in the attached table. The numbers on the sides indicate the number of tiles in rows, columns, or diagonals.
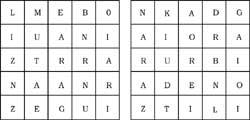
38º Find 14 Basque villages (left) and 10 rivers (right). The letters of the names must be together, by vertices or by parts.
39. In the adjacent product all asterisks are the first numbers, but what?.

40. Along the road there are four villages. The reds live alongside the greens, but not with the whites, the blues do not live alongside the whites. What are the neighborhoods of the whites? :
- Reds
- Greens
- Red and green
- Not known





