¿Música, azar o sabiduría?
Introducción
La música, la de los juegos de los vascos, no la descubriremos aquí. Nuestro objetivo no es inventar nada nuevo. Pero intentaremos hacer un pequeño análisis matemático (probabilístico). Como en todos los juegos de azar, el azar tiene mucha influencia, pero si el juego es correcto todos tenemos que ser la misma suerte. Por lo tanto, aparte del azar, el conocimiento y la experiencia son muy valiosos.
Las probabilidades de los pares y puntos para este artículo, tanto en cuatro como en ocho reyes, las hemos calcado y nos apoyaremos en ellos. No se han tenido en cuenta las probabilidades unitarias de los cuatro jugadores, ni las probabilidades de los casos después de la mus. Por lo tanto, el estudio será muy superficial.
Normativa
Cuatro jugadores intercalados en dos parejas. Se reparten cuatro cartas. El orden de las cartas va desde uno hasta el rey. Cuatro apartados: grande, pequeño, pares y juego (o punto), se juegan separados:
- grande: las cartas más altas (reyes, caballos, gorros...)
- pequeña: cartas más bajas (de una, de dos, de tres,...)
- pares: cartas iguales pares dos cartas iguales medias tres cartas iguales dúas o cuatro cartas iguales
- Juego: los valores de las cartas se suman al punto: Prioridad 30 o menos: Juego 30, 29, 28,.... Más de 30 prioridad: 31, 32, 40, 37, 36, 35, 34, 33 a) Una vez repartidas las cartas, los jugadores deben decir si hay mus o no de la mano. b) Si hay mus, los jugadores podrán guardar las cartas que deseen y modificar al menos una de ellas. De nuevo al punto a). c) Si no hay música, las cartas no se pueden modificar. d) El sistema de apostar en cuatro partes es el mismo: los jugadores pueden saltar o pasar (guardando orden); si una pareja golpea envite, la otra tendrá tres opciones:
tener (nahi), en este caso al final de la mano se verá quién gana; no tener (no querer), en este caso la pareja que ha golpeado el envite tomará un punto; tocar más, subir la apuesta. En este caso la otra pareja podrá elegir entre tener, no tener o tocar más. En esta ocasión, si tenemos la última apuesta, al final de la mano se verá quién es el ganador, o si una pareja retrocede (no la tenga), el otro recibirá todos los puntos de la apuesta hasta entonces.
e) El envite es dos puntos. La apuesta puede ser tan grande como se quiera, pero toda la jugada se toca ahí para apostar. f) Antes de golpear a la pared y al juego hay que saber si tienen pareja o juego. Para poder golpear el envite es necesario que al menos un jugador de parejas diferentes tenga pareja o juego. Si los cuatro jugadores no juegan se juega a puntos. g) Si se pasa a la mayor, a la menor y al punto en su caso, el ganador final recibirá un punto. Si pasamos a la pared y al juego no se puntúa. Sin embargo, la pareja con mejor pareja o juego recibe puntos:
pares = 1 media = 2 duples = 3
juegos 31 puntos = 3 resto = 2
Si una pareja golpea el punto por envite y la otra no lo tiene, la primera toma una y dos puntos.
h) Las jugadas se juegan a 40 puntos (a veces a 30 puntos). i) En estas normas se encuentran cuatro reyes y cuatro reyes. Sin embargo, hay otra alternativa a jugar, con los dos por uno y los tres por el rey, es decir, con ocho reyes y ocho por uno (uno y dos), cuatro, cinco, seis y siete, gorras, caballos y reyes (reyes y tres).
Diccionario
Como todos los juegos, la música tiene su propio vocabulario. A continuación se muestra la base.
Cuando una vez repartidas las cartas se decida si hay música o no:
Esku: a la derecha del jugador que ha repartido las cartas. Postre: reparto de cartas. Mus: el jugador quiere cambiar varias cartas. No hay música: el jugador no quiere cambiar sus cartas. Con la mano: la pareja de la mano coincide con la mano. En general significa que hay mus. Mira: la pareja del postre pasa la decisión al póster (mus o no).
Sin música:
Paso, pues, el jugador no apuesta. Envite: 2 puntos apostar. Más envite, 7 más: a la apuesta anterior el jugador añade 2, 7 más. Hordago: el jugador apuesta toda la mano. Si se acepta, se ve en el momento. Izan, nahi: el jugador acepta la apuesta, se verá al final de la mano. No quiero: el jugador no acepta la apuesta.
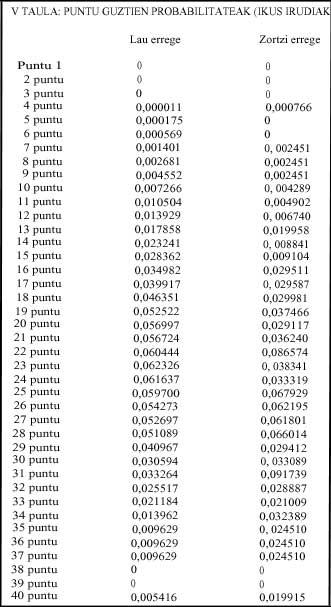
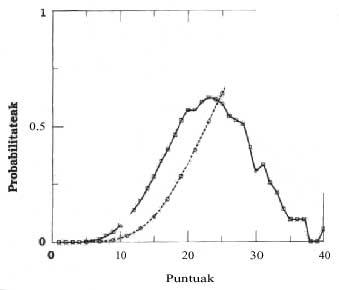
En las figuras 1 y 2 se muestran las probabilidades de los puntos a cuatro y ocho reyes respectivamente.
El punto más probable a los cuatro reyes es 23 con una probabilidad de 0.623, disminuyendo las probabilidades a ambos lados (línea continua). Es evidente el punto 31, donde la probabilidad sube un poco, luego baja. La probabilidad del punto 31 es 0,033.
En la figura 1 se puede ver también la línea discontinua. Esta línea discontinua explica las probabilidades acumuladas. Por ejemplo, la probabilidad de tener 23 o menos puntos es de 0,520. Esta línea nos dice que la probabilidad de tener 30 o menos puntos es de 0,871, o lo que es lo mismo, la probabilidad de jugar es de 0,128.
En la segunda imagen, referida a los ocho reyes, la línea continua cambia radicalmente. Lo más destacado, por el cambio y por su importancia en el juego, es la probabilidad del punto 31, siendo en este caso el mayor 0,091. El otro cambio significativo es el de 22 puntos, cuya probabilidad asciende a 0,086. En el juego, la probabilidad del punto 40 aumenta considerablemente.
La línea discontinua, en este caso, nos dice que la probabilidad de no jugar es 0, 732 y que la probabilidad de estar es de 0,267.
Descripción de tablas
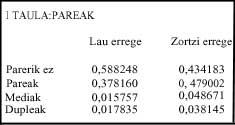
- Tabla: En la siguiente tabla se muestra la probabilidad de cada tipo de par en cuatro u ocho reyes. Los casos son independientes, es decir, si un jugador tiene medias, si tiene un par de ellos sólo lo tomaremos como media. Lo mismo si tiene duples.
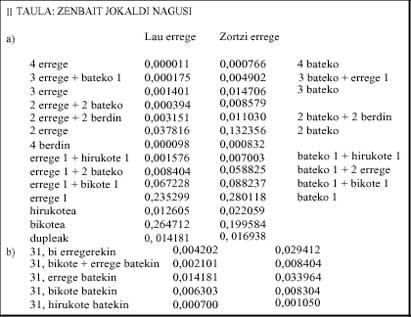
- Tabla: esta vez podemos ver las probabilidades de algunas de las principales jugadas. Estos casos también son independientes. Por ejemplo, en el caso de dos reyes no se incluye el caso de dos reyes y dos ases.
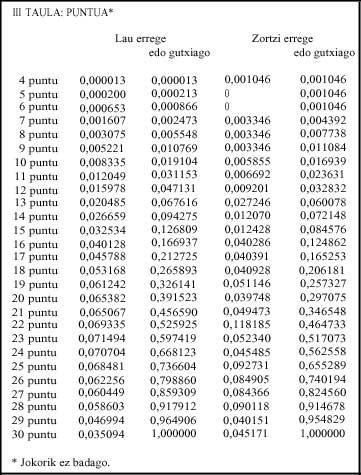
- Tabla: si no hay juego, es decir, en el punto aparecen las probabilidades de los puntos.
- Tabla: Considerando que hay juego, se explica la probabilidad de la igualdad de juego.
Comentarios
La probabilidad de no tener un par a cuatro reyes (0,588) es mayor que la de tenerlo. La ausencia a ocho reyes (0,434) es menor (Tabla I).
Obsérvese que en el mus de ocho reyes la probabilidad de las medias es superior a 0,048 (Tabla I), en duples, 0,038. En cambio, en el mus de cuatro reyes es mayor que el de los duples, 0,017, el de los medios, 0,015. Esto nos dice que la musa de ocho reyes es más directa que la otra, ya que se valora más el caso menos probable.
La probabilidad de que haya juego es de 0,128 en cuatro reyes y de 0,267 en ocho.
En el juego ocurre al revés. En el mus de ocho reyes la probabilidad de 31 aumenta considerablemente (0,091) respecto al cuadrado (0,033). Como se puede observar en la tabla IIb, las probabilidades de todas las combinaciones que se presentan para obtener 31 son menores en el mus de cuatro reyes que en el zortziko. Por lo tanto, podríamos decir que la música de cuatro reyes es más directa.
A cuatro reyes, si todos los jugadores tienen menos de 31 puntos, es decir, si no hay juego, la mitad de la probabilidad de ganar la apuesta se consigue con 22 puntos. P(22 o menos) = 0,525 (Tabla III).
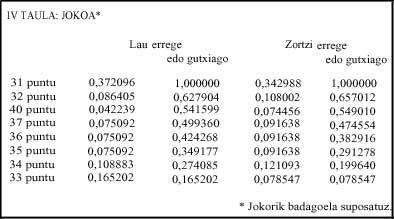
En el juego, es decir, si al menos un jugador de dos parejas tiene más de 30 puntos, la probabilidad es mayor que el 31, 0,033; de entre todos los juegos (31, 32, 40, 37, 36, 35, 34, 33) un tercio de las probabilidades (0,372) (Tabla IV). En este caso se supera la mitad de las probabilidades de ganar la apuesta con 40 puntos; P(40 o menos) =0,541.
A ocho reyes, si no hay juego, es decir, si todos los jugadores tienen entre 4 y 30 puntos, con 22 puntos no llega a la mitad de la probabilidad de ganar la apuesta. P(23 o menos) = 0,517 (Tabla III).
En caso de juego, la mayor probabilidad es de 31, 0,091; 0,342 de los juegos. Por último, la mitad de las promesas de ganar la apuesta se consigue con 40 puntos: P(40 o menos) = 0,549.
Para finalizar, hay que decir que las probabilidades no aseguran los casos y por lo tanto no puedes fiarte. Sin embargo, al igual que la experiencia, ayudan. Esperamos que disfrutes de este artículo y aprendas a comportarte mejor.