Music, chance or wisdom?
Introduction Introduction Introduction Introduction
The music, that of the Basque games, we will not discover it here. Our goal is not to invent anything new. But we will try to make a small mathematical analysis (probabilistic). As in all gambling, chance has a lot of influence, but if the game is correct we all have to be the same luck. Therefore, apart from chance, knowledge and experience are very valuable.
The odds of the pairs and points for this article, both in four and eight kings, we have calmed them and will rely on them. The unitary odds of the four players, or the odds of cases after the mus, have not been taken into account. Therefore, the study will be very superficial.
Rules of Procedure
Four players interspersed in two pairs. Four cards are dealt. The order of the cards goes from one to the king. Four sections: big, small, pairs and game (or point), are played separately:
- big: the highest cards (kings, horses, caps...)
- small: lower cards (of one, of two, of three,...)
- Pairs: Equal Cards Pairs Two Equal Cards Half Three Equal Cards or Four Equal Cards
- Game: the values of the cards are added to the point: Priority 30 or less: Game 30, 29, 28,.... More than 30 priority: 31, 32, 40, 37, 36, 35, 34, 33 a) Once the cards are dealt, players must say whether or not there is a mus at hand. b) If there is mus, players can save the cards they wish and modify at least one of them. Back to point a). c) If there is no music, the cards cannot be modified. d) The system of betting in four parts is the same: players can jump or pass (keeping order); if a couple hits send, the other will have three options:
have (nahi), in this case at the end of the hand will see who wins; not have (not want), in this case the couple who has hit the send will take a point; touch more, raise the bet. In this case the other couple can choose between having, not having or playing more. On this occasion, if we have the last bet, at the end of the hand you will see who is the winner, or if a couple goes back (do not have it), the other will receive all the points of the bet until then.
e) Sending is two points. The bet can be as big as you want, but the whole move is played there to wager. f) Before hitting the wall and the game you have to know if you have a partner or game. To be able to hit the envite it is necessary that at least one player of different couples have a partner or game. If the four players do not play, points are played. g) If you move to the major, the minor and the point in your case, the final winner will receive a point. If we move to the wall and the game is not scored. However, the couple with the best partner or game gets points:
Pairs = 1 mean = 2 double = 3
Games 31 points = 3 rest = 2
If a couple hits the point by sending and the other does not have it, the first takes one and two points.
h) The moves are played at 40 points (sometimes at 30 points). (i) In these rules are four kings and four kings. However, there is another alternative to play, with the two by one and the three by the king, that is, with eight kings and eight by one (one and two), four, five, six and seven, caps, horses and kings (kings and three).
Dictionary of the English dictionary
Like all games, music has its own vocabulary. The base is shown below.
When once dealt the cards are decided whether there is music or not:
Esku: to the right of the player who has dealt the cards. Dessert: cast of cards. Mus: the player wants to change several cards. There is no music: the player does not want to change his cards. With the hand: the pair of the hand coincides with the hand. In general it means that there is mus. Look: the pair of the dessert passes the decision to the poster (mus or no).
Without music:
Step, then, the player does not bet. Send: 2 points bet. More send, 7 more: to the previous bet the player adds 2, 7 more. Hordago: the player bets all the hand. If accepted, it is seen at the time. Izan, nahi: the player accepts the bet, will be seen at the end of the hand. I do not want: the player does not accept the bet.
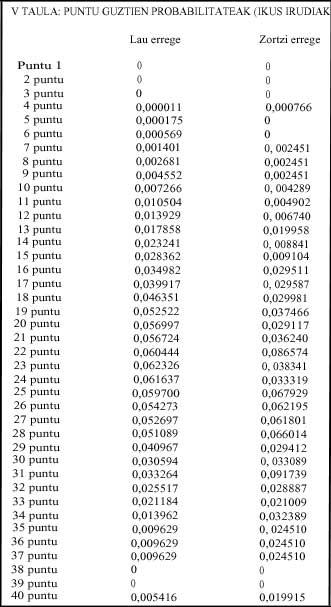
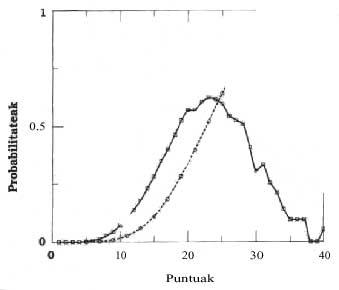
Figures 1 and 2 show the odds of the points to four and eight kings respectively.
The most likely point to the four kings is 23 with a probability of 0.623, decreasing the odds on both sides (continuous line). It is clear point 31, where the probability rises a little, then decreases. The probability of point 31 is 0.033.
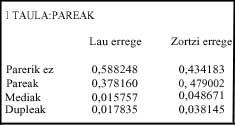
Figure 1 also shows the discontinuous line. This discontinuous line explains the accumulated probabilities. For example, the probability of having 23 or fewer points is 0.520. This line tells us that the probability of having 30 or less points is 0.871, or what is the same, the probability of playing is 0.128.
In the second image, referring to the eight kings, the continuous line changes radically. The highlight, for the change and for its importance in the game, is the probability of point 31, being in this case the greater 0.091. The other significant change is that of 22 points, whose probability is 0.086. In the game, the probability of point 40 increases considerably.
The line discontinuous, in this case, tells us that the probability of not playing is 0, 732 and that the probability of being is 0.267.
Description of tables
- Table: Table: The following table shows the probability of each type of pair in four or eight kings. The cases are independent, that is, if a player has means, if he has a pair of them we will only take it on average. The same if you have doubles.
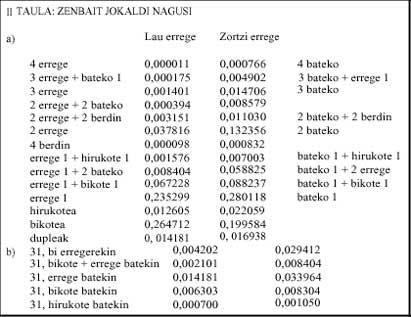
- Table: this time we can see the odds of some of the main moves. These cases are also independent. For example, in the case of two kings, the case of two kings and two aces is not included.
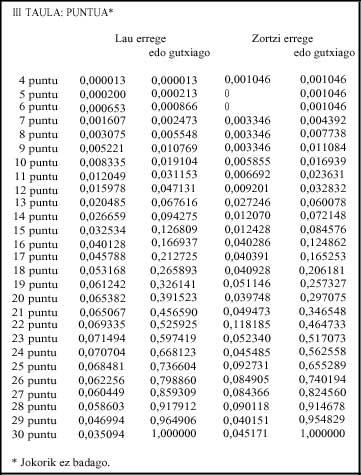
- Table: if there is no game, that is, in the point the probabilities of the points appear.
- Table: Table: Considering that there is game, it explains the probability of playing equality.
Comments Comments Comments
The probability of not having a pair of four kings (0,588) is greater than that of having it. The absence of eight kings (0.434) is lower (Table I).
Note that in the mus of eight kings the probability of means is greater than 0.048 (Table I), in doubles, 0.038. On the other hand, in the mus of four kings is greater than that of the twins, 0.017, that of the media, 0.015. This tells us that the muse of eight kings is more direct than the other, since the least probable case is valued more.
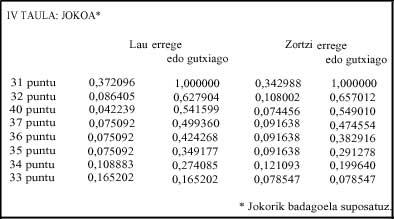
The probability that there is a game is 0.128 in four kings and 0.267 in eight.
In the game it happens backwards. In the mus of eight kings the probability of 31 increases considerably (0.091) compared to the square (0.033). As can be seen in Table IIb, the odds of all combinations presented to obtain 31 are lower in the mus of four kings than in the zortziko. Therefore, we could say that the music of four kings is more direct.
To four kings, if all players have less than 31 points, that is, if there is no game, half the probability of winning the bet is achieved with 22 points. P(22 or less) = .525 (Table III).
In the game, that is, if at least one player of two pairs has more than 30 points, the probability is greater than 31, 0.033; of all games (31, 32, 40, 37, 36, 35, 34, 33) a third of the probabilities (0.372) (Table IV). In this case, it exceeds half the odds of winning the bet with 40 points; P(40 or less) = 0.541.
To eight kings, if there is no game, that is, if all players have between 4 and 30 points, with 22 points does not reach half the probability of winning the bet. P(23 or less) = .517 (Table III).
In case of play, the highest probability is 31, 0.091; 0.342 of the games. Finally, half of the promises to win the bet are achieved with 40 points: P(40 or less) = 0.549.
To finish, it must be said that the odds do not ensure the cases and therefore you cannot trust. However, like experience, they help. We hope you enjoy this article and learn to behave better.