Maurits Cornelis Escher (II)
Partición periódica da superficie

Non hai temas tan atractivos como a partición periódica da superficie Escher. A este tema ofreceulle un amplo tratado que dicía: É a fonte de suxestións máis rica que atopei e aínda está moi lonxe de esgotarse.
En 1922, baixo a dirección do mestre de Mesquita, realizou na súa madeira un debuxo con oito cabezas (catro en voz) cubrindo toda a superficie. Esta idea, con todo, non é imputable a Mesquita (figura 1).
Até 1926 parecía que este tema era una época de mocidade. Con todo, tras visitar a Alhambra de Granada en 1926, Escher tentou dotar ás súas imaxes dunha estrutura rítmica que non logrou o obxectivo. En 1936 volve visitar a Alhambra con Jetta. Con axuda de Jetta copiaron as súas imaxes. Tras a lectura de libros sobre adornos e algúns tratados matemáticos, en 1937 Escher desenvolveu un sistema práctico que escribiría en 1941 e 1942.

Mediante translacións, xiros e movementos de reflexión podemos conseguir que una imaxe axústese a si mesma. Algunhas imaxes só permiten a translación, outras a translación e xiro, etc. En total son 17 as imaxes que permiten estes movementos sen modificar. Escher conseguiu todos, aínda que non tiña coñecementos matemáticos paira iso.
As particiones de Escher caracterizábanse por que os temas elixidos paira repetilo sempre indicaban algo concreto. A este respecto dixo: Os árabes conseguiron una gran mestría enchendo a superficie con imaxes repetitivas. Desgraciadamente, o islam prohibíalles as imaxes. Ningún artista árabe atreveuse a utilizar imaxes coñecidas como elementos decorativos como paxaros, peces, réptiles ou persoas. A limitación ás formas xeométricas paréceme inaceptable, xa que a posibilidade de coñecer imaxes é a razón fundamental do interese permanente que teño nesta materia.

Escher non traballou coa partitura como tema principal. En cambio, utilizaba a partición como ferramenta en metamorfose e ciclos. Aínda que nalgún traballo só traballou a metamorfose (Metamorfose I), na maioría dos casos mesturaba metamorfoses e ciclos. No libro A partición periódica da superficie apareceu en 1958, Escher explicou con mestría as diferentes situacións dunha metamorfose (Figura 2):
- Na fase 4, a imaxe está dividida en paralelogramos brancos e negros.
- Na fase 5 as liñas divisoras cambian de cor e comezan a dobrarse, correspondendo a un prego exterior outro interior.
- Nas fases 6 e 7 séguese o mesmo proceso mantendo a imaxe obtida na fase 7 até a súa finalización. Non existen restos de paralelogramos orixinais. Con todo, é a mesma superficie e tampouco se desprazaron os puntos de contacto entre as imaxes.
- Na fase 8, os detalles introducidos en figuras negras converten ás aves en aletas, facendo das caras brancas a do ceo.
- Na fase 9, con todo, as aves brancas atópanse sobre fondo negro, cubrindo o curado da noite.
- Na fase 10, por que non se pode cubrir a superficie con aves brancas e negras?
- A fase 11 pode admitir dúas interpretacións diferentes. Representando o ollo e a boca na cola das aves e convertendo a cabeza en cola, as ás convértense automaticamente en ás, converténdose en peixes voadores.
- Por último, na fase 12 aparecen simultaneamente dous tipos de animais: aves negras cara á dereita e peixes brancos cara á esquerda.

A metamorfose II, 1939-40, é a maior imaxe de Escher. As dimensións do debuxo son de 4 m de lonxitude e 20 cm de alto. En 1967 ampliouse seis veces e Escher alargou 3 m paira instalarse nunha Oficina de Correos. Este traballo dinos que a técnica da metamorfose Escher non se alargaba demasiado. É sorprendente ver como se poden extraer as lagartijas dos cadrados paira convertelas en hexágonos.
A imaxe máis admirada é o Día e a noite (1939). O cambio entre o día e a noite de dereita a esquerda é lento e a subida do chan ao ceo é lenta pero segura.
Entre os ciclos atópase a litografía Ciclo de 1938, na que a partición ten tres puntos de simetría diferentes. Nun deles recóllense as tres cabezas, no segundo os talóns dos tres pés e o terceiro é o punto de contacto dos tres xeonllos (figura 3). Outro, Anxos e demos (1941).

Neste caso, a partición periódica ten una simetría cuádruplo. En todos os puntos nos que os extremos das ás tócanse entre si podemos facer un xiro de 90º ata que a imaxe axústase a si mesma (Figura 4). Con todo, non todos os puntos son iguais. Os puntos A, P, Q, R e S son diferentes dos puntos B, C, D e E. Tamén podemos trazar a liña horizontal e vertical desde os eixos de todos os anxos e demos, sendo todos os eixos de simetría. Por outra banda, pódense trazar rectas que pasan polas cabezas dos anxos e que forman un ángulo de 45º cos eixos anteriores. Estes non son eixos de simetría correctos, pero si una vez realizada a reflexión sobre un eixo transfórmase na súa dirección, a imaxe non cambiará. Esta versión será reutilizada máis tarde por Escher paira elaborar limites circulares e esferas.
Paira terminar diremos que en 1942 Escher fixo un pequeno selo. En todos os lados do cadrado pódense ver tres enlaces. O selo pódese imprimir en catro posicións. Con este selo e o seu inverso Escher realizou diferentes deseños (figura 5).
Perspectiva

A perspectiva clásica obríganos a imaxinar paralelos ao cadro. Estas liñas, por tanto, non teñen puntos de escape, ou o que é o mesmo, o seu punto de corte está en infinito. Pola contra, a nosa experiencia mira una torre desde abaixo, na que as liñas verticais viran cara a un punto. Este punto é cenit. Se a mirada é descendente aparece o punto nadir. Este punto foi explicado por Escher no debuxo realizado na madeira da torre de Babel de 1928 [1] e no de San Pedro de 1935, Roma [2]. Esche-r utilizouno por primeira vez en 1946 como punto de escape nun "ex libris" (Sairemos).


Outro mundo I, 1946 [3], e Outro mundo II, 1947 [4], tentou en imaxes que Escher fose o cenit, o nadir e o mesmo punto de escape. O primeiro non lle gustou porque o punto desaparecía na escuridade dun túnel. Na segunda, con todo, conseguiu suxerir este triplo punto mediante tres xanelas dobres igualitarias. Una ao intervalo que se ve por diante outra se ve por baixo e a última por encima, sendo o punto de escape do primeiro, o cenit do segundo e o nadir do último punto.

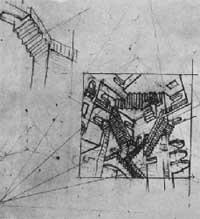
Con todo, na litografía de relatividad (1953) hai tres puntos de escape, formando un triángulo equilátero de 2 metros fose do cadro (Figura 6). Aquí reuníronse tres mundos totalmente diferentes. Aínda que non o pareza, podería facerse un modelo tridimensional da imaxe [5]. Os 16 seres que aparecen pódense dividir en tres grupos: os que están de pé paira nós, os que teñen a cabeza á esquerda e os que teñen á dereita. Dous das tres escaleiras situadas na parte central poden ser utilizadas polas persoas en pé. Poden facelo outros grupos?. Na escaleira superior hai dúas persoas de todo o mundo formando un ángulo recto. Pode suceder o mesmo noutras ocasións?

Por arriba e por abaixo no debuxo as liñas verticais son curvadas e non rectas como indica a perspectiva tradicional (figura 7). Esta é a novidade dos Eschers en perspectiva. As liñas curvas axústanse mellor á nosa percepción do espazo. Como se lle ocorreu a Escher substituír as liñas rectas por curvadas? Paira responder a esta pregunta vexamos a figura 8. Una persoa observa as liñas paralelas que forman os fíos entre dous postes. Os puntos máis próximos son P e Q. Se miramos cara adiante, veremos que se dirixen cara ao punto V1 e mirando cara atrás cara ao punto V2. Mantendo a continuidade das liñas, aparecen liñas curvas.
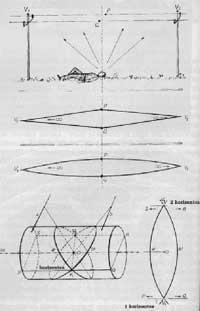

Pero a que lei xeométrica séguense estas liñas?, que tipo de curvas son?, son segmentos de círculos, hiperbolas ou elipses?. O esquema móstrase na figura. Se o ollo está no punto Ou, o que o ve veo na superficie dun cilindro e os fíos a e b no cilindro ven como a' e b' elipse. Estas medias concéntranse nos puntos de fuga V1 e V2. Paira representar todo isto en dúas dimensións, cortando o cilindro polas liñas PQ e RS e planeando a superficie superior, convértense en a' e b' sinusoides. Escher chegou a este resultado de forma intuitiva porque non sabía o que eran sinusoides.
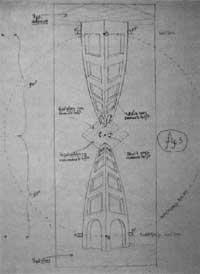
É un dos mellores traballos desde arriba e abaixo [6]. O punto central é o nadir da parte superior e o cenit da inferior. Como dixemos, as liñas verticais son curvadas, pero todas elas van cara ao centro. Paira poder entender ben esta imaxe é necesario cubrir una primeira metade (superior ou inferior) e logo a outra. Así, darémonos conta de que desde dous puntos de vista diferentes (arriba e abaixo) vemos o mesmo.
O pavimento central aparece tres veces: arriba como teito, abaixo como lodo e no centro como teito e lodo. Esta zona media é o que nos sorprende. Se pasamos de arriba a abaixo a liña central, pódese pasar de estar no chan a colgar e viceversa. A parte superior non é un espello da inferior. Escher buscaba nesta imaxe dous efectos: o primeiro, curvar as liñas verticais (e varias horizontais) e o segundo, concentrar o nadir e o zenit no mesmo punto.
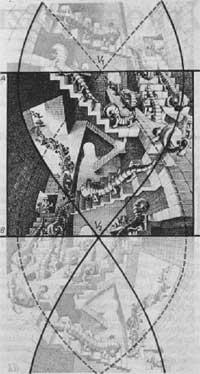
Utilizou a mesma perspectiva na litografía Caixa de escaleiras (1951) (Figura 9). Representáronse varias liñas da estrutura que subxace á imaxe. Isto pon de manifesto os dous puntos de escape desde os que se debuxaron as liñas horizontais. Con cada animalito de dispositivo pódese determinar se o punto de escape é cenita, nadir ou o punto máis afastado. Por exemplo, paira o gran animalito do medio V1 é o punto máis afastado e V2 é o nadir.
De aquí dedúcese que, paira cada animalito, as paredes da caixa terán diferente significado (teito, tezo ou muro).
O tramo entre A e B ten elementos básicos. As partes superior e inferior da imaxe construíronse mediante reflexos.
Alguén podería pensar que a perspectiva cilíndrica que utilizou Escher podería estenderse á esférica. Escher non o fixo, pero por que non?





