Maurits Cornelis Escher (II)
Periodic surface partition

There are no topics as attractive as the periodic partition of the Escher surface. To this subject he offered a broad treatise that said: It is the richest source of suggestions I have found and is still far from exhausted.
In 1922, under the direction of the master of Mesquita, he made in his wood a drawing with eight heads (four in voice) covering the entire surface. This idea, however, is not attributable to Mesquita (Figure 1).
Until 1926 it seemed that this theme was a time of youth. However, after visiting the Alhambra in Granada in 1926, Escher tried to give his images a rhythmic structure that did not achieve the objective. In 1936 he revisited the Alhambra with Jetta. With the help of Jetta they copied their images. After reading books on ornaments and some mathematical treatises, in 1937 Escher developed a practical system that he would write in 1941 and 1942.

Through translations, twists and reflection movements we can get an image to fit itself. Some images only allow translation, others translation and rotation, etc. In total there are 17 images that allow these movements without modifying. Escher got them all, although he had no mathematical knowledge for it.
Escher's partitions were characterized by the fact that the themes chosen to repeat it always indicated something concrete. In this regard he said: The Arabs achieved great mastery by filling the surface with repetitive images. Unfortunately, Islam prohibited the images. No Arab artist dared to use images known as decorative elements such as birds, fish, reptiles or people. The limitation to geometric forms seems unacceptable to me, since the possibility of knowing images is the fundamental reason for my permanent interest in this matter.

Escher did not work with the score as the main theme. Instead, he used partition as a tool in metamorphosis and cycles. Although in some work only metamorphosis (Metamorphosis I) worked, in most cases it mixed metamorphosis and cycles. In the book The Periodic Partition of the Surface appeared in 1958, Escher masterfully explained the different situations of a metamorphosis (Figure 2):
- In phase 4, the image is divided into black and white parallelograms.
- In phase 5 the dividing lines change color and begin to bend, corresponding to an exterior fold another interior.
- In phases 6 and 7 the same process is followed by maintaining the image obtained in phase 7 until its completion. There are no traces of original parallelograms. However, it is the same surface and the contact points between the images have not been moved either.
- In phase 8, details introduced in black figures turn birds into fins, making white faces the sky.
- In phase 9, however, white birds are on a black background, covering the curing of the night.
- In phase 10, why can't the surface be covered with black and white birds?
- Phase 11 can support two different interpretations. Representing the eye and mouth in the tail of the birds and turning the head into tail, the wings automatically become wings, becoming flying fish.
- Finally, in phase 12 two types of animals appear simultaneously: black birds to the right and white fish to the left.

Metamorphosis II, 1939-40, is Escher's greatest image. The dimensions of the drawing are 4 m long and 20 cm high. In 1967 it was expanded six times and Escher extended 3 m to settle in a post office. This work tells us that the Escher metamorphosis technique was not too long. It is surprising to see how the lizards can be extracted from the squares to convert them into hexagons.
The most admired image is Day and Night (1939). The change between day and night from right to left is slow and the rise from the ground to the sky is slow but safe.
Among the cycles is the lithograph Cycle of 1938, in which the partition has three different points of symmetry. In one of them are collected the three heads, in the second the heels of the three feet and the third is the contact point of the three knees (figure 3). Angels and demons (1941).

In this case, the periodic partition has a quadruple symmetry. At all points where the ends of the wings touch each other we can make a turn of 90º until the image adjusts itself (Figure 4). However, not all points are equal. Points A, P, Q, R and S are different from points B, C, D and E. We can also draw the horizontal and vertical line from the axes of all angels and demons, being all axes of symmetry. On the other hand, straight lines can be drawn that pass through the heads of the angels and form a 45º angle with the previous axes. These are not correct symmetry axes, but if once the reflection on an axis is made it becomes its direction, the image will not change. This version will later be reused by Escher to develop circular boundaries and spheres.
Finally we will say that in 1942 Escher made a small seal. On all sides of the square you can see three links. The seal can be printed in four positions. With this seal and its reverse Escher made different designs (figure 5).
Perspective

Classical perspective forces us to imagine parallels to the painting. These lines therefore have no escape points, or what is the same, their cut-off point is infinite. On the contrary, our experience looks at a tower from below, in which the vertical lines turn towards a point. This point is cenit. If the look is descending the point nadir appears. This point was explained by Escher in the drawing made in the wood of the tower of Babel of 1928 [1] and in that of St. Peter of 1935, Rome [2]. Esche-r used it for the first time in 1946 as an escape point in an "ex libris" (We will leave).


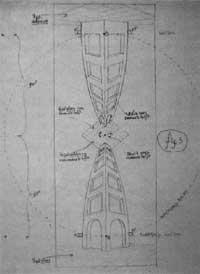
Another world I, 1946 [3], and Another world II, 1947 [4], attempted in images that Escher was the zenith, the nadir and the same point of escape. The first did not like it because the point disappeared in the darkness of a tunnel. In the second, however, he managed to suggest this triple point through three egalitarian double windows. One at the interval seen ahead another is seen below and the last above, being the escape point of the first, the zenith of the second and the nadir of the last point.

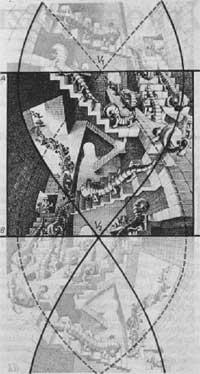
However, in the lithograph of relativity (1953) there are three escape points, forming an equilateral triangle of 2 meters outside the picture (Figure 6). Here three totally different worlds have come together. Even if it does not seem, a three-dimensional model of the image could be made [5]. The 16 beings that appear can be divided into three groups: those who stand for us, those who have the head to the left and those who have to the right. Two of the three stairs located in the central part can be used by people standing. Can other groups do it?. On the upper staircase there are two people from all over the world forming a right angle. Can the same happen on other occasions?

Above and below in the drawing the vertical lines are curved and not straight as the traditional perspective indicates (Figure 7). This is the novelty of the Eschers in perspective. Curved lines better fit our perception of space. How did Escher think of replacing straight lines with curved lines? To answer this question, see Figure 8. A person observes the parallel lines that form the threads between two posts. The closest points are P and Q. If we look forward, we will see that they are heading towards point V1 and looking back towards point V2. Maintaining the continuity of the lines, curved lines appear.
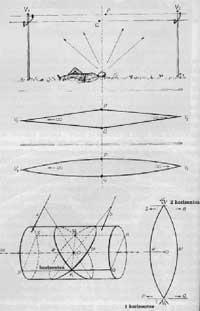

But what geometric law do these lines follow? What kind of curves are they? are they segments of circles, hyperballs or ellipses? The outline is shown in the figure. If the eye is at point O, the one who sees it sees it on the surface of a cylinder and the threads a and b on the cylinder look like a' and b' ellipse. These stockings are concentrated in leakage points V1 and V2. To represent all this in two dimensions, cutting the cylinder by the PQ and RS lines and planning the upper surface, they become a' and b' sinusoids. Escher came to this result intuitively because she did not know what they were sinusoids.
It is one of the best works from above and below [6]. The central point is the nadir at the top and the zenith at the bottom. As we have said, the vertical lines are curved, but all of them go towards the center. To be able to understand this image well it is necessary to cover one first half (upper or lower) and then the other. Thus, we will realize that from two different points of view (above and below) we see the same thing.
The central pavement appears three times: up as ceiling, down as mud and in the center as ceiling and mud. This middle zone is what surprises us. If we pass from top to bottom the center line, we can move from being on the ground to hanging and vice versa. The top is not a mirror of the bottom. Escher sought in this image two effects: the first, bending the vertical lines (and several horizontal ones) and the second, concentrating the nadir and zenit at the same point.
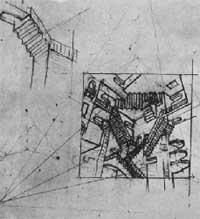
He used the same perspective in the lithograph Stair Box (1951) (Figure 9). Several lines of the structure underlying the image have been represented. This highlights the two escape points from which horizontal lines have been drawn. With each gadget animalito you can determine if the escape point is cenita, nadir or the farthest point. For example, for the great animalito of the medium V1 is the furthest point and V2 is the nadir.
From here it follows that, for each animalito, the walls of the box will have different meaning (ceiling, yew or wall).
The section between A and B has basic elements. The upper and lower parts of the image have been constructed by reflections.
Someone might think that the cylindrical perspective Escher used could extend to the spherical. Escher did not, but why not?





